Bonjour,
Je souhaiterai profiter de la hauteur de mon garage pour réaliser un plancher afin de stocker du matériel encombrant mais pas très lourd (transat, carton vêtement...)
Mon garage fait 4 m de large, je compte fixer des solives le long de 2 mur afin d'y fixer des sabots.
ces sabots permettront de soutenir d'autres solives qui constitueront la base du plancher.
dans un premier temps, il n'y aura très certainement pas de plancher a proprement parlé. Il n'y aura que les "poutres".
Je précise qu'il n'est pas du tout envisagé de marcher sur cette structure.
voici un schéma pour compléter le tout.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAA4MAAAHbCAYAAABx1U9JAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAACVySURBVHhe7d27VtvMwgbg4b8WSJGVKzBXYNKkSpsOSmjSfWW6NLiEbrepaAJXgK8gK0XwvfB7dLBlI4MBSZY1z7OX9ueDLEuymcnrOejgcS4AAACQlP8r/gsAAEBChEEAAIAECYMAAAAJEgYBAAASJAwCAAAkSBgEAABIkDAIAACQIGEQAAAgQcIgAABAgoRBAACABAmDAAAACRIGAQAAEiQMAgAAJEgYBAAASJAwCAAAkCBhEAAAIEHCIAAAQIKEQQAAgAQJgwAAAAkSBgEAABIkDAIAACRIGAQAAEiQMAgAAJAgYRAAACBBwiAAAECChEEAAIAECYMAAAAJEgYBAAASJAwCAAAkSBgEAABIkDAIwLsdHBwsFgBgPxw8zhW3AeBVyvBXrUrqHgMA+kcYBOBNYuh7rgp56XkAYLd0EwXg1bYJevH5spUQAOgfYRCAV9HiBwDDIAwC0BqtgwDQX8IgAFt7S6ugQAgA/SQMAgAAJEgYBGAr7xkrqHUQAPpHGAQAAEiQMAh74S6cHRyEg4PjMJkVD0GH3tMqWNI6CE0p64RiObsrHs/dnVWeOzibr92hu7PO33dxvMeTsKmKjOusnaaF2eQ4f/2mFWDAhEHYA3dnJ+G6uA0AK/78q4SgWfj3p7iZgBjyTq5Pw+3jbTidXoSjJ4FuFibHcZ3i7rrZJHy7mIbR5UN4vBoXD0I6hEHou7uzzZUYdCD+Yv7eVkGgHaPRKITp3/BQ3A/zW3+nxeMJGF89zsunqzCe/+9qXk69OtAdnof7+evuzw+LByAtwiD02ixMfmyZBGeTcJx1zTkOk7vydlyKrjqL5yuPQcd0FYVmffr0af7/f8K/smnw7ibrSZI/XrXsWrrSePakW2dlWMKkfG7zEIVFF8uVbTy1ut5BON5mzMNi34qlrhvoSt0Wl+q+xlbBo3AxD8fR9Ul8frmPb9onGBhhEHpsNvmWVWKjy8twWjz2smm4OLmY/3/pOpzEiu5o7TFjIwD235cv8/phGn79zoPMLOsjehoffqd5XXJR/Bg5+ho+1zScxTB1VCatzLxuqenKErtyrq433/rF0bPhKwtq69uK3UCrgTCGxZW6LZrv99Hm8YGlt+wTDJEw2JHqL0+WtJetFeMY5kkw/O/8Q/Hglk5vsxaYx9tlhMzGQ8wfe7gsug5d32z8BRdK8TvbdBdRrYPQpKPwMespmncUfcj6iH6cP9qAsi65Pw9Ps+Bd+FmGqXK9x4dQVjEL87os7+ASx/XFdeJym/3AOb34uaEeWm67rLvK14Tpr5Dn3rtwVobFxfsv67jrk9gCeBjO75f7dHob17kK4zftEwyTMAi9NAuTb/mvnaf/1VXCzxmFy+/FmImjj/N70Sh8LX7WPfyw3nXobaoB1zLc5a2fNdCVw5AV69kkMsXkMZ8+vLLeqHf65Znxd7N/IZ+nZh6oFuP05uHrv7V+LA9/i5a7opdKtpSTol2Hm7rkVdn2f4uxfMWYwMf7kD1U+/5xCOB/WajbuO3oLfsEAyUMQh/d/czHOJzeBpObAfCco7xpMDyUk8d8bKJdcBSe3cwiUK1Z/AiZy7utvtKmbVdtXCdvKY3+LAZSrnrTPsFACYMdKbsvWCzbuLspur5cn6z9YpmPhXj9tZA+hQ9N/EwMDYl/C/G7Dbxf3uPjT/g3KSaP6aLAX4S+yuQ10aaQNroMD2v1YVxqf/BcC5S1Nq6TB+LoxfPwmn2CgRIGgTdZrzwtw1ve8zkDHRrnk8jkE76chvrencsWs+tFP8hXzFi97vBDyAcdzN/35+btHX7+moe26UVYrPbShekX274OPxYTusSZQfMundkkL5V1qhOizSY/ih9Pn56HsqXwTfsEAyUMQg/l102qLsXA+Xn1dfkwv+9nSwAWlkFv8+QxxdjCaNHrZHnZhdcbh++LCcme2d7heSiHEeaXdpgvxcQvo8vv863UWW47zvC5uu1yHOE4XJWTpC3efzlD6OltvPZgtDzufFvHYRLesk8wTMIgAMBeqwS9ZyaPGV+tz/Z5Gm4rs06/1uH5/XKG6kz99uIPnOsPx1lCn7vQe9x2dUbsTNatswx5c+Or8PhwudZdNP/RtPqb6fj7+jpv2ycYooNH/XkAWBN/Ke+ieujqfQCAp7QMAgAAJEgYBAAASJAwCMAKXTcBIA3CIAA7E0NnDJ8AQPeEQQAAgAQJgwAAAAkSBgEAABIkDAKwsIvJY4wbhP65OzvI/i7L5eyueAIYFGEQAICFGARPros7hesTgRCGSBgEAKBwF26KIHh6+5i13N+e5vevb6RBGBphEACAwjhczQNgDIFX4+Khl8wm4TjrTnocJnfl7biczaNl9fnKY0AvHMz/2F1ZGIDsH2q7rBJ2/f7Amhjiji7CNN4eXYaH+/NwmD2xprreNk5vw+PWSRNok5bBluS/flksFsv+LE2WXcDATH+F37Pi9nNi0Isti2Xf0rnR5UP22MPlKH/g+kbrIPSEMAgAwFOH5+F+Eeym4eLopS6eo3D5vWjxO/o4vxeNwtfPeXvi4YdP2X+B/hAGAQDYbPwl5O18f8K/bVoHgb0hDAIAkLs7K7p7NzXRy6fwoXagIdAHwiAAvRDHFBlvCDu26N55HX5M8mbA2eTH/F4k2MHQCIMdygZUWywWSw+X95RRwIAcnof/FRO9TC+Osh9oji7yeUJHl9+DOUBhWIRBAAAWDs/vlzN/FuIF6O/PNQvC0OztdQarXYn6eAh1XZ38gg70VSyz3lpGNVnevWc/AIDX0TIIAACQIGEQAAAgQcIgQOL61DUz7kddt1MAoHnGDLakyTE0AG16bxhsurx77/7sm7rzBwDr2qgbtQwCAAAkSBgEAABIkDAIAACQIGEQAAAgQSaQaUnTEyoAtKGJyVraKO+a2K99ob4AYF1XdYOWQQAAgAQJgwAAAAkSBgEAABIkDAIAACRIGAQAAEiQMAgAAJAgYRAgUX2+fEPcr7pptQGA5giDAAAACRIGAQAAEiQMAgAAJEgYBAAASJAwCAAAkCBhEAAAIEHCIECC+nxZiZLLSwBAu4RBAACABO1lGKz+Utz3X7YBAAD6SMsgAABAgoRBAACABAmDAAAACRIGAQAAEiQMAgAAJEgYBEjMPlxjsORagwDQHmEQAAAgQcIgAABAgoRBAACABAmDAAAACTp43JdZBCqqkwn0dffrJjzYtK8mRwCGqKnyeZ8mvHmL19QXAKShq7pByyAAAECChEEAAIAE6SbaEt1+gL5quttl2+Vd0/vbN+oLANZ1VTdoGQQAAEiQMAiQkH1sZYv7W/cLKQDwPsIgAABAgoRBAACABAmDAAAACRIGAQAAEiQMAgAAJEgYBAAASJAwCAAAkCBhEAAAIEHCIAAAQIKEQYBEHBwchMfHx+Lefon7HfcfAGiOMAgAAJAgYRAAACBBwiAAAECChEEAAIAEHTzu4WwC1UkE+rr7dRMd7OvEDcAwtDWBTFflXVv7v2t15w8A1rVRB2oZBAAASJAwCAAAkCDdRFvSVbcpgG211c2yq/Kurf3ftbrzV6XuAEjLpnqhjfpAyyAAAECChEEAAIAECYMAAAAJMmawJV2NoQHYRpvj7bos79o8jl2pO39VTR7vS+/1Huo4eLs2/zbfwt/zbm36PrTxuQiDLan7EP1hAbsSy6S2yqAuy7s2j2NX6s5fVZPH+9J7vceuP5c2jy3q4/fO59mc1I73JX38vqdk0/ehjc9FN1EAAIAEaRlsSV2i9ysLsCuxTGqrDOqyvGvzOHal7vxVNXm81fdqYrtNb+89XjqP79XH712bxzz0z3Ndn453V/vSp7/nTbr+XrykrfO06TjbeD9hsCV9+7ICdKnNCnIPq61nvVRfNHm8TdeffaqP29iXPh1fHZ/n+6R2vC/p0/nYpLqPfdDFd7OqjffTTRQAACBBwiAAALBXYivZLpah0U20JXXNu0P8AgH7IZZJbZVBXZZ3bR7HrtSdv6omj7f6Xk1st+ntvUcb+9Kn46vj83yf1I73JX06H5ukcp6q71HVxvtpGQSAilgJlwsADNnehcEu0jgAREIhAEOmZRAAXiAUAjBEwiAAbEkoBGBIhEEA2GDTcASBEIAhEAYB2Gtla11Ty7oYCOtC4ab1AWBfCIMAAxcDy1An3OoyjAmFAAyNMAjA3ohhbNfBSygEYCj27qLz1Yq2z7te9w+CPTvVwEDE8qjN8qfr8q56PH2oE+qOP9p2fza9vtTkcTV9vvpw/ktt7Eufjq+Oz/N9Ujvel/TpfGxS3cc+6OK7WdXG+2kZBIB32FQ5x8q8b/9wgX1U/i01vQDzv695JdbP6L9B9Y+3z7teV8js2akGBiKWR22WP12Xd9Xj6VudUHcuSpv277nXRE0e10vv9R67Pv9tfBf69v1al8rn2YUhfn9fq+/f96jr78VL2jpPm46zjfcTBltS9yHu2akGBiKWR22WP12Xd9Xj6WudUHdOSuv7+dy6UZPH9dJ7vceuz3+bxxb16ftV8nk2p0/Hu6t96cM+kNv0/W/jcxEGW1L3IfrDAnYhlkdtlj9dl3fV4+l7nbDNualbp6rJ43rpvd5j1+e/zWOL9uX71ZQ+Hu+Qtf39fS2f/25t+j608bkIgy2p+xD9YQG7EMujNsufrsu76vH0tU6oOyel9f18bl0AKLVRz5lABgAaEoPdpnAXK/E+BVYAEAYBoAFCIAD7RjfRltT9o8A/BoBdiOVRm+VP1+Vd9Xjq3rsJr9n/Tfuw7Ta6Pn8pqZ5b55S2+J7Rhq7qBi2DALAmVsJ1FXHVpnViZe0fhADsA2EQAF5BCNwP1c/I5wJQTzfRlmz6hwJA12J51Gb503V51+XxVN+n7jhL79mfrs9fKjZ9jtA03zXa0FXdoGUQAJ4RK+S6SjmKFbN//AGwr4RBANhACARgyIRBANiSEAjAkAiDAPACIRCAIRIGAQYsdnMUYt5OCARgyIRBAPZKDGebxvI1oQyAQuD+qn4/fI4Am+1dGFRJAwAAvJ+WQQAAgAQJgwAAAAkSBgEAABIkDAIAACRIGAQABsNMogDbEwYBAAASJAwCAAAkSBgEAABI0M7C4N3ZQdavv1zO7oonAAAAaN3B4w5GV8cgeHJd3Kk4vX0MV+Pizp6rDmAHSFGb1UssY4cyOUhdfWHik7ernk/nkS74ztGGruqGHbQM3oWbIgjG8BcP6vY0v399o3kQAACgCzsIg+NwNQ+AMQRu3Qo4m4TjeTo+ODgOk7vydlzO5tGy+nzlMQAgKVpoAF5nJ91EF2KIO7oI03h7dBke7s/DYfbEmup62zi9DY877m/aVdMuwHNiWdR22bOL8q6L4+qK+qI51XPpHNIV3zva0FXd0J/ZRKe/wu9Zcfs5MejNT8Rj2bd0bnT5kD32cDnKH7i+0TrYkvjFLBcAAGB/7TYMHp6H+0Wwm4aLo5e6eI7C5feixe/o4/xeNApfP+ftiYcfPmX/BQAA4Hn9aBkcfwl5O9+f8G+b1kF2QmsgAAAMR/dh8O6s6GbY1EQvn8KH2oGGNGk9COoTDwAA+637MLjo3nkdfkzyZsDZ5Mf8XiTY9ZEgCEDfVesq9RTAdroPg4fn4X/FRC/Ti6Os8D66yOcJHV1+DwO55vxgCIIAADBMOxkzeHh+v5z5sxAvQH9/rlmwTwRBAAAYrt1eZ3DA1oNUtG+nWhiE/Rf/jtv+291FedfFcXVlCPVFH1TPo/NHl3z3aENXdUM/ZhOld9a/gAo3AAAYFmGQJwRBGIb4t+zvFwDYRBhkhSAIAABpEAZZEAQB2EfV+kvdBbC9vQ6DsfAvF5qlMgX6LJZRyn4AeB8tg2T8owoAANIiDPIkCGoVBACA4RMGEycIAgBAmoTBhAmCAACQLmEwUYIgAACkTRgEAPZW9cdNP2wCvI4wmCCtggAAgDCYGEEQAACIhMGECIIAAEBJGEyEIAgAAFQJgwkSBAEAAGEwAeutggAwBNX6zQ+dAK8nDA6c7qEAAEAdYXDABEEAAGATYXCgBEEAAOA5wuAACYIAAMBLhMGBEwQBAIA6wuDArLcKAgAA1BEGB0T3UABSUa3z1HcAbyMMDoQgCAAAvIYwOACCIAAA8FrC4J4TBAEAgLcQBgEAABIkDO4xrYIAAMBbCYN7ShAEIFXVOlD9B/B2wuAeEgQBAID3Egb3jCAIAAA0QRjcY4IgAADwVgfzQLG3iaLPYwbWW/AAUtN2uRzL2SH8KFZXXwzhuNrU5/qf9Pg+0oau6gYtgwAAAAkSBgEAABKkm2hLmmraXd/OHn9cQMdi+dFFmdFVV5Z1XR1f23Z1/vZV9Xw5T/SB7yRt6Kpu0DLYY+tfAgUMAADQFGEQAAAgQcJgT2kVBAAA2iQM9pAgCAAAtE0Y7BlBEAAA6IIw2COCIAAA0BVhsCcEQQB4XrWuVE8CvJ8wCAAAkCBhsAe0CgIAAF0TBndMEAQAAHZBGNwhQRAAANgVYXBHBEEAAGCXhMEeEAQB4HlmEgVonjC4A+utggAAAF0TBjumeygAANAHwmCHBEEAAKAvhMEdEQQBAIBdEgZ3QBAEAAB2TRgEAABIkDDYMa2CAPA6LisB0A5hsEMqMAAAoC/2OgxWw5Vr9wEAAGxPy2ALBFMAAKDvhEEAAIAECYMN0yoIAADsA2GwQYIgADTLTKIA7REGGyIIAgAA+0QYbMB6EPTLJQAA0HfC4DsJggAAwD4SBhskCAIAAPtCGHwH4wQBAIB9JQy+ke6hAADAPhMG30AQBID2VetbdS1A84TBVxIEAQCAIRAGX0EQBAAAhkIYBAAASJAwuCWtggAAwJAIg1sQBAEAgKERBl8gCAIAAEMkDD5DEASA3ajWwepfgHYIg1tSEQH0RwwKymUAeB9hcIP1VkEAAIAhEQZr6B4KAAAMnTC4RhAEhiKWX3o5AACbCIMVgiAAAJAKYbAgCAJAP1TrZPUxQHuEQQAAgAQJgzX8CgkAAAydMFiIAbBcoGo2Oc66LGXL2V0Id2fF/bMwv7dwd1asUy7HkzArnps/G86yx4/DZFK+fn67WOH51+a23Y+V9ebLcfkmAABQIQzCM2KwOrqYFvfmrk/Cwcl1cWcphrknD08vwlEMbSum4eKiWHH0NXw+3O61r9mPlfXmphdHAiEAAE8Ig7DRXfhZBqvT26Ll+CFcjvKHlu7CTZbLTsNt2cJ8e5o9E65vVlrtMuW27s/D4Vav3XI/ZpPwY31bj7fzezEQ/ny6H0BvVVv3U1yq6p63WPq0VNU9b7G8ZemKMAibzP6FP9mNUbj8Ps5uhXl8O/+vCGsL43CVBa+rMJ4HsuP4R1zTalc6/VJuK9ritdvux8PfkEfG63CyKExO5vfyx26kQQAAKoRB2GQRrj6FD4fZjdzRx3ksW7UY83d0Ubxmk1H4eFTcLLz42i33Y/Yvj4wAALANYRA2WYStP+FfdcjdIpwV7s4WY/5Ob4vumWVXz9HHsJb9Vm3z2m33ozS6DA9Za+PqclVtkAQAIHnCIGxy+CF8ym5Mw8XPso/lLEzygXkLixa5eQgre3He5QMBX7TVa7fcj8PPX/PQOL0Ii9U2zDgKAADCIGw0Dt/LWVri7J1ZqDoKv1Y6Z8aslke1bAbQbJ3K7KDTv+GhuFlnu9dutx/h8DyUwwivT/JtleMPR5ff51sB+mi9FT/1parueYulb0tV3fMWS1NLG4RBeMbh+X14qE7beXob7v8rAlxpfLW6TjabZz6L55Ouneu2fO1W+zE3vnoMZS/T0ujyIdyfVwcbAgBACAfzlLnXV1mPrR+lPh1Kdb9Ke36qKSyu+RfH5mWXh9iNvuwH/RbLorbLnl2Ud10cF7vR13odNvGdZZ9pGYSN7sLZvICPhXx1KS/qPvr6uaMA1pf9AGhXLNtK/lEN0D5hEDaK1wAsu2yu6rbrZV/2AwCAIdFNtCXV/Sr5lRPoWiyL2i57dlHedXFcdK+vdTo8x/eWfdZey+BiSvty2Ty1fRz7tLruQTh7svKyq9zT5ypmk3CcrXccJrNZmBwX29zwosUFv48nYbahO97qYop+AABg/7USBrNwt5gfv3QdTp4EqTyslWOfqrKp8bOA9h6H4fPXYgbG65uaEDcLi8u8GXcFAAAkpIUwOAu/fxUTW1w+ZM3lj4vxTtfhx2QZ72aTb6HMgae3letolHPjTy/Ct8r6b7G4EPf8vW/W0+Dsd8h3dRS+fl6Ngiv7s7JcuV4bAACw9zqaQGYcvpT57m95Ce678LNIgjF4XVUT1vhqEQinFz/f1y3z8HMoGwf/rF3wbfb7V8iz4NewlgUBAAAGrYUweBg+FNfCnl4cLcbYxYthZy1rZeq7uwl5R9LT8KWuqW385cmFt99m2VV0+ut3pdvpsgXz9D/XaAOAXYrj8kvx3wsAtK+VlsHxVXUa/DhWMJ98pXYOl9HHcFTcXHUUPmYZbhoWjYlvtOgqOv0VfpdpcNFFtD6MZmMWF5PGLJfjd3ZbBQAA6IOWuonG66I9hofLon9mIQasnYSpRVfRafhVpMFFF9HTL8YAAgAAyWl1zODh+X0x6cqypfDJGMDp31Df8PcQ/uYD+sLH+qbDV3jaVfQh3/g8C9ZHwU0TyLjANwAAMATNh8HF9QWrl5EYh6uHy2JWz2IM4GJM4OoMo6XZ5EcxpvBT+NBA/lp2FY3h8y7cZBvfMF4RgN6KdUz8cQ4AeJ/mw+CGkLfolrkId5UZRi+OVscTzgNlee3B0eX3ZrpxLrqKXoebs2LyGl1EAQCARLXQTXQcvhdjBfPZRPOJV+rC3fjqIZTDClcmbCkvWD+6DP+r6ZZZXbfq+fGIy66i19fFPKbPNAtumkDm4OA4mEMG2BexBS2WXQAA61oZM5iNFSwvHF8RL0K/OubuMJzfP51oJsouWH/f7CUflhegj3QRBYA+qP5goQswQHcO5oXuXpe6fa1A6n6JV8EBuxDLozbLn67Lu7aPh+71tS6Hbfj+ss9anU0UAACAfhIGAQAAEiQMAgAAJEgYBAAASJAwCADsjMk3AHZHGAQAAEiQMAgAAJAgYRAAACBBwiAAAECChEEAAIAECYMAAAAJEgYBgJ1wWQmA3RIGAQAAEiQMArA3YkuSFiQAaIYwCDBwMTxVu+MBAETCIAAAQIKEQQAAgAQJgwBA58wkCrB7wiAAAECChEEAAIAECYMAAAAJEgYBAAASJAwCAAAkSBgEAABIkDAIAHTKZSUA+kEYBAAASJAwCAAAkCBhEAAAIEHCIEAC4ris6jitfRT33/gyAGiOMAgAAJAgYRAAAN4o9lgoF9g3wiAA0BmXlQDoD2EQAAAgQcIgAABAgoRBAACABAmDAAAACRIGAQAAEiQMAgCdMJMoQL8IgwAAAAkSBgEAABIkDAIkInbLq3bT2ydxv3UrBIBmCYMAAAAJEgYBABiOu7OsN8FyOQt3xVPrZpPjtXUPwtmTle/C2cbnKmaTcJytdxwms1mYHBfb3PCiu7Pi+eNJmFXeY/OyfhxPX1P/Vk2vx5AIgwAADEIW7k6ui3ul63DyJEjlYe3oYlrcX7o+mQehLKC9x2H4/HWU37y+WXvvaBb+/clvjb5+nq/9SlnwPJkf2aq478eTyp43vR6DIwwCAK2LrQwl4z9pxyz8/pWHu9HlQ/Y9e3y8DafZI9fhRyXUzCbfQpkDT2/jesVym68dphfh2ztD0OHnryGPg9fhZj0Nzn6HfFdH4evn1Si4sj8ry1UYZ2vMg+y3i5C//DI8lM8X+z69+BbyXW96PYZIGAQAYKDG4UuZ7/4+5DfCXfhZJMEYvK7yhJUbX1VC0M+aFr1XOPwcysbBP/9W09Ts968ifH0Na1nwZZUgefm/82Wr4vhLEXynITvUptdjkIRBAAAG4DB8+JTfml4chXKM3fiqaOkqU9/dTdEd8jR8qQbB0iIE/QlrGe6Vll1Fp79+h+Wmli2Yp/9Vwte2Ds/DfdZ6dx/OKy+eTX4UxzUKH4/m/2l6PQZJGAQAYBDGV2W30CiOFXxmIpTRx1CfcY7CxyzDvb9FbNFVdPor/C7T4KIlrj6MZmMWi/2uLs+N3YuT0ZTjH0eX/1sJdVVNr8f+EwYBABiIcbh6fAwPl0X/zMLOJkJZdBWdhl9FGlx0ET39UowBfJ8Y3Mo5c2K31/sNya3p9RgGYRAAgEE5PL/Pu4YuJpCJXUfXxgBO/4b6hr+H8DdLa010j3zaVfQh3/g8C9ZHwU0TyNSGstkk/KgEt5Xxj1VNr8dgCIMACYn/oIjdjfZJ3N+43+yv6nfOZ0lrFtcXrF5GYhyuHi7zrprlGMDFmMDVGUZLy7Fyn8KHBhrFll1FY/i8CzfZxjeMV3yzbbfX9Hrsu70Pg9VKZd/+gQMAQEM2hLxFt8xFuKvMMHpxtDqecB4ol2PlvjfSjXPZVfQ63JwVk9c01EV0OflLedmJDZpej8HQMggAwACMw/dirGA+m2g+8UpduBtfPYRyWOHKhC3lYLnRZfhfTbfMt0zuMk9Yi66i19f59jd1EY02vcfBwfHT6/1lF4uPz61fVH9N0+sxGMIgAACDkI0VLC8cXxEvQr865u4wnN8/nWgmyi5Yf/+GSz48Y3kB+kgXTPrj4HEAnffjryWlvhxOdZ9KxkkAfRDLpybLo7bLu6b3l+71sZ4GQMsgANCyGADLBYD+EAYBAAASJAwCAAAkSBgEAABIkDAIQG+ZPAYA2iMMAiQmhqu6GUABgLQIgwAAAAkSBgEAABIkDAJAiu7Osu7Cy+Us3BVPPTGbhONn17sLZyvberqcbdj4bHK81bp3Z6vr1C3Hk1mxNgDbEAYBIDFZADu5Lu6VrsPJhkA4+/0rTIvbcb2bjalxs+uT9ZA3C5Pjg3B0sdxyKa57cDyZrwFAm4RBAEjKLPz+lQew0eVDNqHQ4+NtOM0euQ4/nrSuleuPwunpKHvk+pk0eHobt1ddHsJl/rKV180m30KZA1dec5vvSZhehG+VfRlfVdZ5uJzvTTQKlw/Lx+/PD7NHAdiOMAgAyRuHL2UG+/uQ3yjNfoc8C34N379/zUPY9c3mLqVPHIbPX4s0+Odf0dp3F34WSTAGwatxdjM3vloEwunFz1e8DwCvJQwC0EtxDFhs7aFph+HDp/zW9OJofp7zrqGLlreVZBazYNFF9NOHcHj4OeS57jVdRSstkV8/z9997u5mvoXoNHxZfbvc+EvRUvkn/NNXFKA1wiBAguI/+mPYIk3jq7JbaBTHCuYTsDyduGUZ5E6z1LZs5dvUVTQb71dsL1+O8u6go8vwv/VunKOP4ai4ueoofMzeZhrWGyoBaI4wCADJGYerx8fwUA7mK8QgtzIjZ9lFtNKCd/j5LV1F56YX4eerXgBA24RBAEjU4fl9MfnKsqWwOk5vOYvosvXw4Ohi8Vhd4+DTCWSWofP6ZG220unfUN/w9xD+Zm8yCh/rmw4BaIAwCAApWVxfsBrMxuFqMUNnOU5v2UV0k+dmFa06PP9vdQzgYkxg3eyl83ee/CjGFH4KH0wQCtAaYRAAUrIhiC1bAYsAtugiunr5hmwpL/+wbVfRxYQxpcrspRdHq2MV52G1vPbg6PL7fE0A2iIMAkBSxuF70W0zn0007/65HsAW4XD0NXxeb52rBMr1xsGnE8jMl/IC96f/hXIOmfFV5fqD1deU69ZNOANAo4RBAEhMNlawbN2riBehzy/cXnM5iBXLlr1tu4pmF7hfuWzFYTi/fzqJTZSte39e874ANOngMfb32HPxl8RSXw6nuk+lAZxqYEBiOdVEudRGedfUvgEAm2kZBEhUDFt1QQ4ASIMwCAAAkCBhEAAAIEHCIAAAQIKEQQAAgAQJgwAAAAkSBgES1scZRV1WAgC6IQwCAAAkSBgEAABIkDAIAACQIGEQAAAgQcIgAABAgoRBgMT1aUZRM4kCQHeEQQAAgAQJgwAAAAkSBgEAABIkDAIAACRIGAQAAEiQMAhAL2YUNZMoAHRLGAQAAEiQMAgAAJAgYRAAACBBwiAAAECChEEAMrucRMbkMQDQPWEQAAAgQcIgAABAgoRBAACABB08DmCQRnWMS18OZ9cXbwbYpdeUxcYLAsBuaBkEAABI0CDCYPxFuVwAAAB4mZZBAACABAmDAAAACRrEBDIANKurSV1MHgMAu6NlEAAAIEHCIAAAQIKEQQCeiF03275eqi6iALBbwiAAAECChEEAAIAECYMAAAAJEgYBqNXmuEHjBQFg94RBAACABAmDAAAACRIGAdioja6iuogCQD8IgwAAAAkSBgHojFZBAOgPYRCAZ7U5qygAsDvCIAAAQIKEQQBe1ETroC6iANAvwiAAAECChEEAtvKe1kGtggDQP8IgAABAgoRBALb2ltZBrYIA0E/CIACtEQQBoL+EQQBe5T1jBwGA/hAGAXi1bQKhVkEA6LeDeUWtpgbgTcpAWK1K6h4DAPpHGATg3aqthKoVANgPwiAAAECCjBkEAABIkDAIAACQIGEQAAAgQcIgAABAgoRBAACABAmDAAAACRIGAQAAEiQMAgAAJEgYBAAASJAwCAAAkCBhEAAAIEHCIAAAQIKEQQAAgAQdPM4Vt9ljBwcHxa2cjxUAAHiOlkEAAIAECYMAAAAJ0k0UAAAgQVoGAQAAEiQMAgAAJEgYBAAASJAwCAAAkCBhEAAAIEHCIAAAQIKEQQAAgAQJgwAAAAkSBgEAABIkDAIAACRIGAQAAEiQMAgAAJAgYRAAACBBwiAAAECChEEAAIAECYMAAAAJEgYBAAASJAwCAAAkSBgEAABIkDAIAACQIGEQAAAgOSH8P1HL5PhAVd7oAAAAAElFTkSuQmCC[/img]
voici mes questions:
- Quelles dimensions prendre pour les solives qui serviront à fixer les sabots?
- quelles dimensions pour les solives du plancher (je pensais 63 * 175. Est-ce suffisant pour une portée de 4m?)
merci pour vos conseils et réponses.
 0
0
 Nouveau sujet
Nouveau sujet
 Répondre
Répondre

 Bloggeur
Bloggeur Bloggeur
Bloggeur Bloggeur
Bloggeur Bloggeur
Bloggeur Membre super utile
Membre super utile Bloggeur
Bloggeur C'est intéressant aussi !
C'est intéressant aussi !
 Autres discussions sur ce sujet :
Autres discussions sur ce sujet :









 Résolu
Résolu 





 S'abonner
S'abonner



 Voir la fiche
Voir la fiche
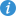 Edité 1 fois, la dernière fois il y a +11 ans.
Edité 1 fois, la dernière fois il y a +11 ans.
 C'est intéressant aussi !
C'est intéressant aussi !





 Autres discussions sur ce sujet :
Autres discussions sur ce sujet :
 Résolu
Résolu



