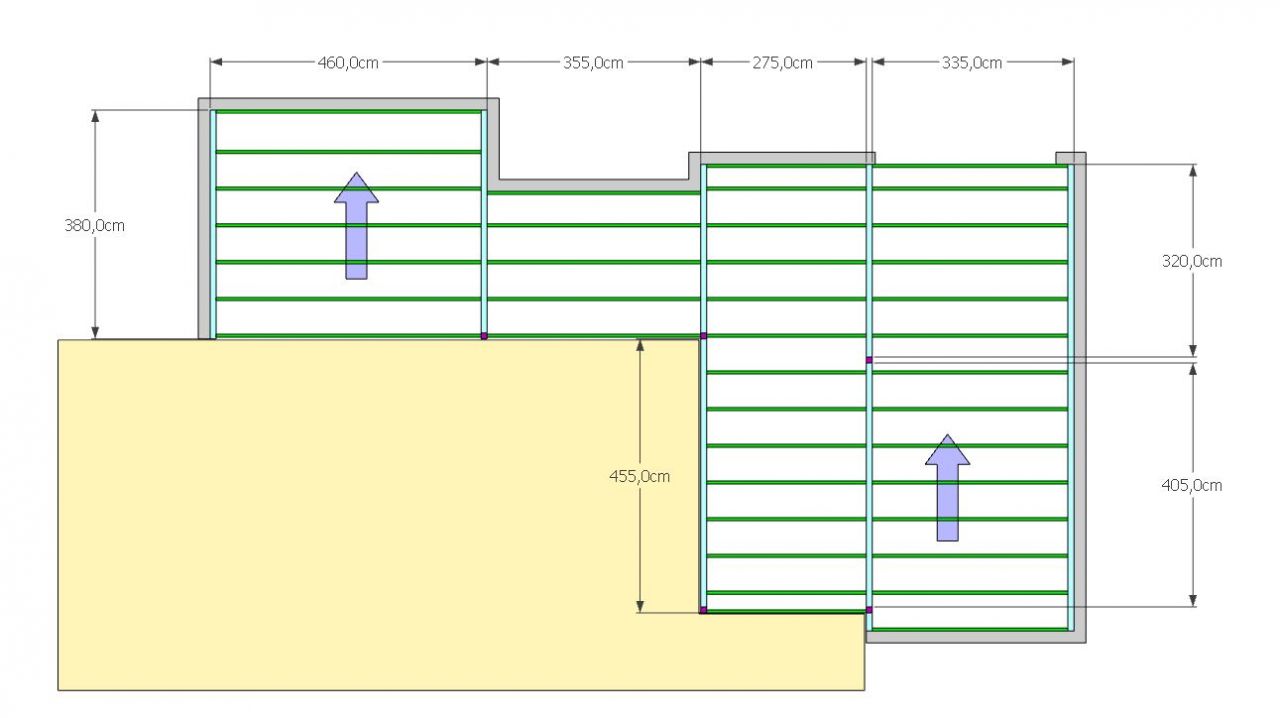
Section charpente toit plat végétalisé - appuis intermédiaires
Ce sujet comporte 8 messages et a été affiché 171 fois
 Nouveau sujet Nouveau sujet
 Répondre Répondre 
|
1 personne surveille ce sujet |
En cache depuis le vendredi 05 décembre 2025 à 11h03
Ce sujet vous a-t-il aidé ?
0
Votez !
0
Votez !
 C'est intéressant aussi !
C'est intéressant aussi !
Devis étancheité toit terrasse
Demandez, en 5 minutes, 3 devis comparatifs aux professionnels de votre région. Gratuit et sans engagement.
Demandez, en 5 minutes, 3 devis comparatifs aux professionnels de votre région. Gratuit et sans engagement.
Mais à toit plat : combien ça coute ?
Les guides vous aident à y voir plus clair sur la construction.
Les guides vous aident à y voir plus clair sur la construction.
21 idées de maisons cubiques à toits plats
L'équipe de Forum Construire sélectionne pour vous les plus belles photos des membres et du web.
L'équipe de Forum Construire sélectionne pour vous les plus belles photos des membres et du web.

1
personne
surveille ce sujet
surveille ce sujet
 Autres discussions sur ce sujet :
Autres discussions sur ce sujet :
-

Abaque de calcul, ai-je juste?
6 réponses Forum Charpente, toiture et zinguerie Résolu
Résolu -

Panne faîtière fissurée et vrillée (garage non attenant à l'habitation)
6 réponses Forum Charpente, toiture et zinguerie -

Quelle hauteur pour la chanlatte ?
7 réponses Forum Charpente, toiture et zinguerie Résolu
Résolu -

Aménagement d'une ferme "paladio" -> dimensionnement des BLC
6 réponses Forum Charpente, toiture et zinguerie -

charpente pour toit plat en bac acier
5 réponses Forum Charpente, toiture et zinguerie -

Avantages et inconvénients de faire des poutres en robinier plutôt qu'en chêne.
6 réponses Forum Charpente, toiture et zinguerie -

Ajout de charge sur charpente de toit plat
2 réponses Forum Charpente, toiture et zinguerie -

Vérification du calcul de la section d'arbalétrier
8 réponses Forum Charpente, toiture et zinguerie -

Section charpente toit plat longueur 6,5m
3 réponses Forum Charpente, toiture et zinguerie





 S'abonner
S'abonner



 Voir la fiche
Voir la fiche


 C'est intéressant aussi !
C'est intéressant aussi !




 Autres discussions sur ce sujet :
Autres discussions sur ce sujet :
 Résolu
Résolu


