Hérisson pour inértie sous dalle portée? Résolu
Ce sujet comporte 7 messages et a été affiché 253 fois
 Nouveau sujet Nouveau sujet
 Répondre Répondre 
|
1 personne surveille ce sujet |
Bonjour à tous. Je construis une extension de 20 m2 en ossature bois. Elle sera collée à ma maison principale qui est de plain pied. Je pense faire une semelle filante avec des fondations en parpaings pleins. Les cotés Ouest et Sud seront en mitoyenneté (Ouest à la maison et Nord au mur en pierre de séparation).
J'hésite :
Soit je fais des fondations qui seront déportées de la semelle et là je peux faire une dalle flottante.
Soit je fais des fondations centrées sur la semelle et je pose dessus une dalle déportée avec un porte à faux d'environ 15 cm.
Voici mes questions :
Quelle est la meilleur solution à ces 2 propositions?
Dans le cas d'une dalle déportée, est il possible de mettre un hérisson afin d'avoir le plus de d'inertie (isolé sous le hérisson et le long du mur du soubassement) ou lorsqu'on fait une dalle déportée (et donc portée) il n'y a aucun intérêt car risque de tassement, etc...
Merci d'avance à tous, ce site est TOP.
J'hésite :
Soit je fais des fondations qui seront déportées de la semelle et là je peux faire une dalle flottante.
Soit je fais des fondations centrées sur la semelle et je pose dessus une dalle déportée avec un porte à faux d'environ 15 cm.
Voici mes questions :
Quelle est la meilleur solution à ces 2 propositions?
Dans le cas d'une dalle déportée, est il possible de mettre un hérisson afin d'avoir le plus de d'inertie (isolé sous le hérisson et le long du mur du soubassement) ou lorsqu'on fait une dalle déportée (et donc portée) il n'y a aucun intérêt car risque de tassement, etc...
Merci d'avance à tous, ce site est TOP.
Je me demande parfois si ce n'est pas perdre son temps que d'essayer de rattraper le temps perdu.
Le chat
Le chat
 0
0  Sujet résolu !
Sujet résolu !
message
Sinon, passe par un pro...
Va dans la section devis maçonnerie du site, remplis le formulaire et tu recevras jusqu'à 3 devis comparatifs de maçons de ta région. Comme ça tu ne courres plus après les maçons, c'est eux qui viennent à toi
C'est ici : https://www.forumconstruire.com/construire/devis-0-7-devis_maconnerie.php
Va dans la section devis maçonnerie du site, remplis le formulaire et tu recevras jusqu'à 3 devis comparatifs de maçons de ta région. Comme ça tu ne courres plus après les maçons, c'est eux qui viennent à toi

C'est ici : https://www.forumconstruire.com/construire/devis-0-7-devis_maconnerie.php
Bonsoir,
On ne doit pas avoir les mêmes définitions pour "fondations", "semelle" ...
si vous pouviez ajouter 1 ou 2 schémas pour illustrer ce que vous envisagez ça pourrait aider
On ne doit pas avoir les mêmes définitions pour "fondations", "semelle" ...
si vous pouviez ajouter 1 ou 2 schémas pour illustrer ce que vous envisagez ça pourrait aider

 0
0  Membre ultra utile
Membre ultra utileBonjour Elisa.
Voici un plan spartiate de mes fondations. Pour résumer je cherche à obtenir le plus d'inertie au sol. Je pensais donc ne pas mettre d'isolant sous ma dalle. Mais, dans cette configuration, j'ai un énorme pont thermique en nez de dalle. Peut être est il possible d'isoler le mur de soutènement par l'extérieur?
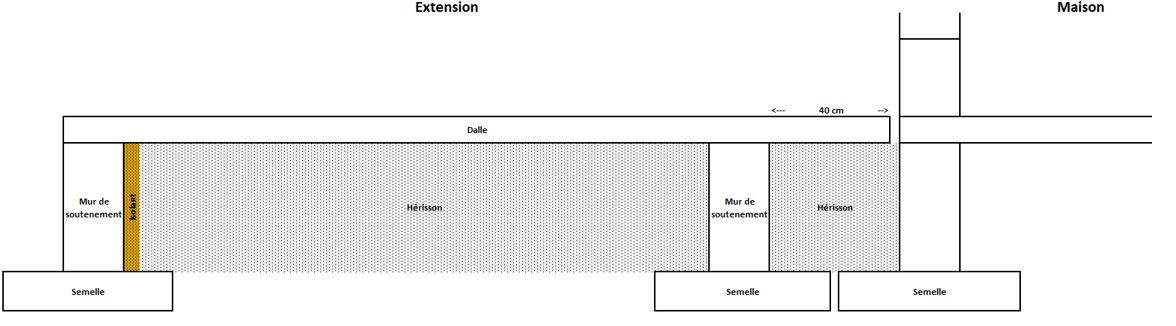
Voici un plan spartiate de mes fondations. Pour résumer je cherche à obtenir le plus d'inertie au sol. Je pensais donc ne pas mettre d'isolant sous ma dalle. Mais, dans cette configuration, j'ai un énorme pont thermique en nez de dalle. Peut être est il possible d'isoler le mur de soutènement par l'extérieur?

Je me demande parfois si ce n'est pas perdre son temps que d'essayer de rattraper le temps perdu.
Le chat
Le chat
 0
0 Bonjour,
Pourquoi parler de mur de soutènement alors qu'il est destiné à supporté une dalle ?? Pour l'intertie je vois pas trop ce que viens faire le hérisson là du coup ? L'inertie vous l'aurez plutôt avec des murs en béton plein par exemple ou en pierre avec isolation par l'extérieur.
Pourquoi parler de mur de soutènement alors qu'il est destiné à supporté une dalle ?? Pour l'intertie je vois pas trop ce que viens faire le hérisson là du coup ? L'inertie vous l'aurez plutôt avec des murs en béton plein par exemple ou en pierre avec isolation par l'extérieur.
 0
0  Membre super utile
Membre super utileBonsoir
merci pour le schéma ; mais il n'explique pas tout :
.
pas "fondations" mais sous-bassement .
pas compris les dalle flottante et dalle déportée avec un porte à faux ...
comment allez vous faire ce porte à faux ? vous écrivez 15cm , le schéma indique 40 ?
Vous envisagez quel type de dalle ?
vraiment dsl mais il y a trop d'inconnues , impossible de répondre sérieusement
"collée" doit être une expression ? les 2 doivent être désolidarisées.
Semelle filante = type de fondations.
autres possibilités pour les fondations : semelles isolées, plots...
voir google image "semelle filante ou longrine"
en remplaçant soutènement par sous-bassement : oui l'isoler est une très bonne idée car très efficace ,
en remontant l'iso jusqu'au nez de dalle.
Cdlt.
merci pour le schéma ; mais il n'explique pas tout :
.
pas "fondations" mais sous-bassement .
pas compris les dalle flottante et dalle déportée avec un porte à faux ...
comment allez vous faire ce porte à faux ? vous écrivez 15cm , le schéma indique 40 ?
Vous envisagez quel type de dalle ?
vraiment dsl mais il y a trop d'inconnues , impossible de répondre sérieusement

"collée" doit être une expression ? les 2 doivent être désolidarisées.
Semelle filante = type de fondations.
autres possibilités pour les fondations : semelles isolées, plots...
voir google image "semelle filante ou longrine"
en remplaçant soutènement par sous-bassement : oui l'isoler est une très bonne idée car très efficace ,
en remontant l'iso jusqu'au nez de dalle.
Cdlt.
 0
0  Membre ultra utile
Membre ultra utileBonjour Tornes et merci pour tes remarques.
Désolé pour mon mauvais langage... je parlais du mur qui est posé sur la semelle et qui supportera la dalle, j'abandonne l'idée d'une dalle flottante.
Pour des questions de facilité et d'accessibilité aux terrains (une toupie à béton ne peux pas s'approcher à moins de 90m de mon chantier) les 4 murs seront en ossature bois. Donc je n'aurai pas d'inertie. C'est pourquoi aller la chercher dans le sol me paraissait le plus judicieux. Mais il y a peut être d'autres solutions?
Je me demande parfois si ce n'est pas perdre son temps que d'essayer de rattraper le temps perdu.
Le chat
Le chat
 0
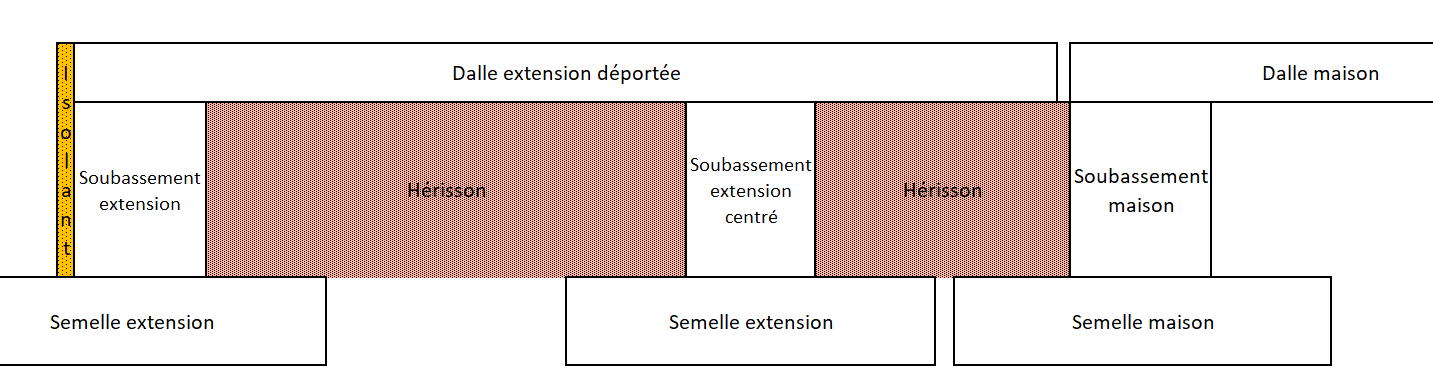
0 Elisa, merci pour tes réponses.
Pour répondre à tes questions je ne sais pas s'il vaut mieux déporter le mur de soubassement de la semelle pour avoir moins de déport de la dalle ou de centrer le mur de soubassement mais avoir plus de déport de la dalle. Qu'en penses tu?
Dans mes recherches, je n'ai pas trouvé de dalle solidarisée sans isolation dessous . Je n'ai trouvé d'hérisson que sous des dalles flottantes...
. Je n'ai trouvé d'hérisson que sous des dalles flottantes...
Je pense tout de même qu'il est intéressant de mettre un hérisson afin d'avoir de l'inertie dans le sol (ça sera une ossature bois). Mais est ce vraiment pertinent et/ou efficace?
 [img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABegAAAF1CAYAAACTcQoTAAAgAElEQVR4AeydPdKruNa2PZgTdNWegZMOO9kjOPEpRx2dCXS8M4edfVEP4CSO33l4MHwlwb0QQmAwCARcXbXbmJ+lpUuLJelGD75V/AcBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMDmBG6bl0iBEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIVAj0BAEEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0GeCfrvdKv7BgBggBogBYoAYIAaIAWKAGCAGiAFigBg4VgysJRPQ7sdqd9qL9iIGiIHdYmCtjgc7XQK7NSgPBngwQgwQA8QAMUAMEAPEADFADBADxAAxQAx8HQPd2f3339AFEPuIAWKAGCAGJsXA910NV44REPzq/27V0n9ma6xAjkEAAhCAAAQgAAEIQAACEIAABCDwNYG1595r2/u6YlwIAQhAAAJFE+AVN5maxzriSKB3+8cE+9Rxs5XJV8xCAAIQgAAEIAABCEAAAhCAAASuTmDtuffa9q7ePtQfAhCAwFkJINBnalnriCOBfkycHzpmtjL5ilkIQAACEIAABCAAAQhAAAIQgMDVCaw9917b3tXbh/pDAAIQOCsBBPpMLauO2H0OCe9u/5TjspXJVcxCAAIQgAAEIAABCEAAAhCAAAQuT2Dtuffa9i7fQACAAAQgcFICCPSZGtY6YlbQZyKMWQhAAAIQgAAEIAABCEAAAhCAwHoEbB6/ksm17a3kFmYgAAEIQKAwAgj0mRrEOuJIoHf7566oN1uZfMUsBCAAAQhAAAIQgAAEIAABCEDg6gTWnnuvbe/q7UP9IQABCJyVAAJ9ppa1jjgS6MfE+aFjZiuTr5iFAAQgAAEIQAACEIAABCAAAQhcncDac++17V29fag/BCAAgbMSQKDP1LLqiN3nkPDu9k85LluZXMUsBCAAAQhAAAIQgAAEIAABCEDg8gTWnnuvbe/yDQQACEAAAiclgECfqWGtI2YFfSbCmIUABCAAAQhAAAIQgAAEIAABCKxHwObxK5lc295KbmEGAhCAAAQKI4BAn6lBrCOOBHq3f+6KerOVyVfMQgACEIAABCAAAQhAAAIQgAAErk5g7bn32vau3j7UHwIQgMBZCSDQZ2pZ64gjgX5MnB86ZrYy+YpZCEAAAhCAAAQgAAEIQAACEIDA1QmsPfde297V24f6QwACEDgrAQT6TC2rjth9Dgnvbv+U47KVyVXMQgACEIAABCAAAQhAAAIQgAAELk9g7bn32vYu30AAgAAEIHBSAgj0mRrWOmJW0GcijFkIQAACEIAABCAAAQhAAAIQgMB6BGwev5LJte2t5BZmIAABCECgMAII9JkaxDriSKB3++euqDdbmXzFLAQgAAEIQAACEIAABCAAAQhA4OoE1p57r23v6u1D/SEAAQiclQACfaaWtY44EujHxPmhY2Yrk6+YhQAEIAABCEAAAhCAAAQgAAEIXJ3A2nPvte1dvX2oPwQgAIGzEkCgz9Sy6ojd55Dw7vZPOS5bmVzFLAQgAAEIQAACEIAABCAAAQhA4PIE1p57r23v8g0EAAhAAAInJYBAn6lhrSNmBX0mwpiFAAQgAAEIQAACEIAABCAAAQisR8Dm8SuZXNveSm5hBgIQgAAECiOAQJ+pQawjjgR6t3/uinqzlclXzEIAAhCAAAQgAAEIQAACEIAABK5OYO2599r2rt4+1B8CEIDAWQkg0GdqWeuII4F+TJwfOma2MvmKWQhAAAIQgAAEIAABCEAAAhCAwNUJrD33Xtve1duH+kMAAhA4KwEE+kwtq47YfQ4J727/lOOylclVzEIAAhCAAAQgAAEIQAACEIAABC5PYO2599r2Lt9AAIAABCBwUgII9Jka1jpiVtBnIoxZCEAAAhCAAAS2IPB6uAUF9+r53qK0fGWcpR75CGEZAhCAAARsHr8SirXtreQWZiAAAQhAoDACCPSZGsQ64kigd/vnrqg3W5l8xSwEIAABCFyYwOvh/5rrHqqvqX0XRnTOqr+r590J74/qNVbB97O6327V7TF61piFMo6dpR5l0MQLCEAAAqclsPbce217pwVPxSAwRCA1L0ntG7qe/RA4CAEE+kwNZR1xJNB3xPl/bvWk9+dn0d7Z4z8IQAACELgYAYmKTiAN/93v1f3xrF5rrGhODXBT+y6Gfml13897/8HHUqOrXj9NoK9XnX8Q8Vf1K4+xs9QjDx2sQgACEICACGi8pe9LP9e2t9QfrofAqgSYqyzCWf58YVH1uHgmAVTfmcCmnq6O2H12RPlQsP+nEVxGBPqOnamFcx4EIAABCJyDgAa993v1eDzsn1/R3Aj2nZXv39Q6Jcan9n1jO/s1r+rhONyf1RrPKtZ0t/wB9wSBvom/chfPT2z/4uuxZuRhCwIQgAAElhDQ/HuJjfDate2FttmGwO4EmKssaoLy5wuLqsfFMwkg0M8ENvV064hDQT7eZgX9VJycBwEIQOCaBDToTSik71fz6pHbrUocns4rJcan9k23uOGZEwXaDT06TlETBPriK0P7F99EOAgBCEDgYARsHr+S32vbW8ktzEBgHQLMVdbhiBUIVFWFQJ8pDKwjjkR5t99W1CcE+s7x5lqzlclXzEIAAhCAQKEERga93uNGSP/4HvGx6qXE+NS+MRu7HUOg/R49Av337LgSAhCAAATOSmDtuffa9s7KnXodlABzlYM2HG6XSACBPlOrWEccCfQmzrv9CYG+cxyBPlPrYBYCEIDAQQh8GvRWElnjVfTv6v16VHf/I6B6f/29eoQ/BCsEKTE+tc+f/65ej3v9+yl6xc79MeNd+BOub8ruvbZGLJrX2dTvFFfdgs/OnxNMKM/VqynTXeq52fv+B5hV7+r1fEQcnt0fWx1jGF17c68wSv2gwGy/1KjR5/tVPR/1O/H9+MS3mWIn9X75OdzulQurON7uj9fAa4f67KbU38VdPba6V8+Xa7Kgza294h+znViPVWI7Ys5XCEAAAhA4JAGbx6/k/dr2VnILMxBYh4DG553xd2ha480DzFXGxt0ap7+f1cPmV8PzhHhcfLsNnJucL/THyvd7NM/wiPvnTRlTT5vrhG3I9lYEEOgzkVZH7D5TorvfxzvoM9HHLAQgAIGTEPg46K2q1LsLbd/9UT1fr+r1ageTvXfWpwaGqX32MKD5gVpn14TmWqQdp64B+ufrJb6GY/16X1DOu66Xfx+/1fMVPCyYXp4Eejeodf32/e7e998+iIiZyT//Q73icA98cyBGGbr35ut3BYJywgoHNqb6lebf/JWBf1d//TsG3Qc3sUA/l9u9une4BQ8u4vpYDM2svxfgXdw8qofj/KrcEwEf16u0v/n1OTbTjNkLAQhAAAJnIaB5/Fr1WdveWn5hBwKrEDjTXKUZu9u42//+lxaI3Kq7Fov4eUI73o3nCUvnYZPmGTZ2nTmm7ozZgzlIahHXKgGCkTkEEOjn0JpxrnXErKCfQY1TIQABCECgQ2DCoDcpBL9f1bv3q6kDr4NJCcmJfRps9jXX5l34vQOdmtiDhN5pyTpKVG7E44Q/tfWBOjn99lkPqCeVpwH5LRLZ5VvnR2gbAbuzr1tX/y3hs3y69ZxSfaPyZ/mV8CHgMDR5iF+PJB97LopFeGDIvypdH9leXH+r6jrtL7/CqvkiUnW2stmAAAQgAIEzErB5/EqVW9veSm5hBgLrEJgyVkqMid1Ci9LmKppTudXuoV6tcaK7lzvjadU9nhMsqtu0eYb51Bu8psfgQ3WrhuqwTnRgZSYBBPqZwKaebh1xJNC7/baiPvGKm85xXnEzFTfnQQACEDgnAQ2aeoOvtroaoHUGjO3hYEsro6MV06lBc2+fBovudTbv6t3596r/1DMenAYlV1rl0bxaZdL1En/d6hW/+vuZeGXKkEA7099efeV8ipn2uZXcvacgujCxgl7XRfybK5LtOMuvtuh2a6zM1LFm39R2GvSvfUDSxmWqvMDT5oFKe/7QXyG011R6ENCLvTn1mHNuWDbbEIAABCBwRgI2j1+pcmvbW8ktzEBgHQKnmauMjDsH6zg+tu0CHji3N5bWeWPzDJ2z5ZyiWxu+5SGAQJ+Ha/Oe1ECMj4R6veLG/2n2z/Hz6NQzNRJmIQABCJROYHBA2DouYbev4bv30D+rp//zzObVJv5VIdFgrjcwTA1QtRpj4L3fgwK6/Pzuev2JZ7ySRVaHBdqZ5aUY+EIGBsDh+yfdq2qeifet92wOPUxoatOc31ld3rOhmg/4pcP2OVZmysZa3EZiqCemf1N/VXCofnPqMedclcsnBCAAAQiclcDac++17Z2VO/U6KIHTzFVSY1e1STNW7E22UmNpXbNgHvZxnjE0/m3KzjKnUL34zEkAgT4TXXXE7tNWzMciPe+gz0QfsxCAAAROQuDjoFcDw+6fYro/Y/QPgL0gH4vqCwR69wNFndXzwWr6UeTtQHL69apb7X9vTOzLa+1217K3+yeV96UQ7h6AhD8UFf45rP6UtF0R3vrU9bUBl2UwPVam+Ibx0J6/jFtqktPaXl5/BduQzXb/53rMOVfl8gkBCEAAAmcloHn8WvVb295afmEHAqsQOM1cJTV2FaFmrNibjKTG0rWdRfOwptjheUY7dl0+ph6og6rO56YEEOgz4baOOBblw++JV9ykxHyzlclXzEIAAhCAQKEEPg16dbyzKlkDrXv16LyCRftDQXZgMNoTrAeunYxt/vX2lwHPZhB6i/z2ZQ8NUGeW16uvKjbNznuSuD5uS/VtBf2BtvGujduS9/ZqoSS7lI3UvtZab2uQW/uKm3YuM257Xv3lyRrtP+6XSuITAhCAAASuQWDtuffa9q7RCtTyMAQ0F2kHfF3Xdbz4ucrYuLsZb/bqmBpDat+CeViXYNWfZ6iM1NyoHYOvO6eInOJrFgII9FmwVoOvuHEdtInwCYG+c7wR8+nUMzUSZiEAAQiUTkCD2t6A0P/6p62S7x4eEi2bd8XHYm1KZE3sSwqo4udX1etL+nPW9aq3BvMpAdwXMzxAnVVeor51LYbtd2uZGLgnbOqVPZ0BszP0bq6PfpSqvwpfpU71y70Kv/4LhG6Z7+r1qH9Ed+hHYrvnN+XG7ax2if3Wu+Gj/Wlfvqn/Zw5z2n/OuSqZTwhAAAIQOCeBtefea9s7J3VqdVgCGrN3JyN1dXTsdqu6h8ucqwyPuxPjfF/D1Hh8hbr1gqFf/npj6lQdeg6wYyMCCPSZQFtHHK6Yj7cTAr2J98G5ZiuTr5iFAAQgAIFCCWhg695z3nuXvBNe3fvP+3/caIO2x7N6vV7V8xm+8iZabZEQktMD1GZweLtV98ezer5e1cu/474WepOCbgfr1Os1UOy+tkd16g7wWwH6dnfv2b9XdzthanljK2bkS8DMt4krp2brGOg1N1a0q3eKqwnXt+pmbSqh/Fb1GCZtOOMJvzqsgy+KIddunpFi4V7d7y6Ggrr5y+Zz0ziltn+3B0e9+qxW/7Z+iotF7R/49V1st/6wBQEIQAACxyagPm2tWqxtby2/sAOBVQhonGnj2vB3rw42Vxkcdzdj485A39FLj8c1NtVcYdY8bOo8Ixi7bjanWCVgMDJGAIF+jM6CY+qI3WdKdPf7eAf9AsJcCgEIQOACBDTojd8lrx8m7WvzDZR39bQV0s3g+OVWTScE2dRgNLXPW65XXnfeq3h/VM/Oq3TG2uXz9YOrmY1FQlD2QrOrWyxyfy7PeztS32dPxF7BpnuQELSpE7aTDGf5NcLdrdAPGbmHC2893Ih5Ojvz6/juPASK/6w39K2OzWX1D+1Fdes8sJpYD29uzrlh+WxDAAIQgMCZCGgev1ad1ra3ll/YgcAqBGx8Xo/DFe9eNH6+qveR5iqD4+55Ar0X7r+eh80Zj64xpk4/ZFglNjAymwAC/Wxk0y5QYhoU54MV8p/OMVvTiuYsCEAAAhCAAAQgkJ/A4EQmf9GUAAEIQAACEMhBYO2599r2ctQZmxCAAAQgsD8BBPpMbWAdcSTEu/1jgnzquNnK5CtmIQABCEAAAhCAwGwCCPSzkXEBBCAAAQiUTWDtuffa9sqmh3cQgAAEIPAtAQT6b8l9uM464kigHxPnh46ZrQ9lchgCEIAABCAAAQhsRgCBfjPUFAQBCEAAAtsQWHvuvba9bShQCgQgAAEIbE0AgT4TcXXE7nNIeHf7pxyXrUyuYhYCEIAABCAAAQjMJ4BAP58ZV0AAAhCAQNEE1p57r22vaHg4BwEIQAACXxNAoP8a3fiF1hGzgn4cFEchAAEIQAACEIAABCAAAQhAAAIFELB5/Eq+rG1vJbcwAwEIQAAChRFAoM/UINYRRwK92z93Rb3ZyuQrZiEAAQhAAAIQgAAEIAABCEAAAlcnsPbce217V28f6g8BCEDgrAQQ6DO1rHXEkUA/Js4PHTNbmXzFLAQgAAEIQAACEIAABCAAAQhA4OoE1p57r23v6u1D/SEAAQiclQACfaaWVUfsPoeEd7d/ynHZyuQqZiEAAQhAAAIQgAAEIAABCEAAApcnsPbce217l28gAEAAAhA4KQEE+kwNax0xK+gzEcYsBCAAAQhAAAIQgAAEIAABCEBgPQI2j1/J5Nr2VnILMxCAAAQgUBgBBPpMDWIdcSTQu/1zV9SbrUy+YhYCEIAABCAAAQhAAAIQgAAEIHB1AmvPvde2d/X2of4QgAAEzkoAgT5Ty1pHHAn0Y+L80DGzlclXzEIAAhCAAAQgAAEIQAACEIAABK5OYO2599r2rt4+1B8CEIDAWQkg0GdqWXXE7nNIeHf7pxyXrUyuYhYCEIAABCAAAQhAAAIQgAAEIHB5AmvPvde2d/kGAgAEIACBkxJAoM/UsNYRs4I+E2HMQgACEIAABCAAAQhAAAIQgAAE1iNg8/iVTK5tbyW3MAMBCEAAAoURQKDP1CDWEUcCvds/d0W92crkK2YhAAEIQAACEIAABCAAAQhAAAJXJ7D23Htte1dvH+oPAQhA4KwEEOgztax1xJFAPybODx0zW5l8xSwEIAABCEAAAhCAAAQgAAEIQODqBNaee69t7+rtQ/0hAAEInJUAAn2mllVH7D6HhHe3f8px2crkKmYhAAEIQAACEIAABCAAAQhAAAKXJ7D23Htte5dvIABAAAIQOCkBBPpMDWsdMSvoMxHGLAQgAAEIQAACEIAABCAAAQhAYD0CNo9fyeTa9lZyCzMQgAAEIFAYAQT6TA1iHXEk0Lv9c1fUm61MvmIWAhCAAAQgAAEIQAACEIAABCBwdQJrz73Xtnf19qH+EIAABM5KAIE+U8taRxwJ9GPi/NAxs5XJV8xCAAIQgAAEIAABCEAAAhCAAASuTmDtuffa9q7ePtQfAhCAwFkJINBnall1xO5zSHh//Vm/g17n3n/cqlck6OuYt5PJV8xCAAIQgAAEIAABCEAAAhCAAASuTkDz77U4rG1vLb+wAwEIQAACZRFAoM/UHtYRR4K7xPrXz1qcv/+8Va9ft8qJ9U6gf/7TF/TNViZfMQsBCEAAAhCAAAQgAAEIQAACELg6gbXn3mvbu3r7UH8IQAACZyWAQJ+pZa0jjgR6t9+J9M8ft+r241a9B45LyHefssUnLIgBYoAYIAaIAWKAGCAGiAFigBggBogBYoAYIAaIAWKAGDhRDGTSpy9vVjdJKLSH216gv92q56/+ivnwPAT6E91sN+qi+4JPYoEYIAaIAWKAGCAGiAFigBggBogBYoAYIAaIAWKAGLhVrKDP9CghDK5YcPff/7lVD7eK3om2P27V48/+avpYnM/kKmYPQKATT//7f1XV/HP7te0++Q4P4oH7QzFAPiAfKBboH+gfyQf1mPsAQz5c3ICAux/CeyLcJl+SL3PEg7e5QWxTxPYEXNvSvttzp0QInJEAAn2mVrVEHb3CJhbr378Cod6tqOcd9Jla5NhmLZ4Q5v0DCT8I4kGFPZyBB0IsQiwPZhQD5APygWIBobEVGm0cdezhIN6vREDxQL4kX26RLxVvK4UvZgojQPsW1iC4A4EDE0Cgz9R4lqgjgd4PBKN9TrR3Qv3YNf66TL5itnwCig0fBwjTCNM8qOFBDX8x01n9iBDZCpESG+gvEJ4UC9wf9f3BWLr88e5WHmpcrXuEfEm+VCzkypfkn63u7u3LsXyyfdGUCAEInIwAAn2mBrVEnRDj41X0+v5wfx71s/9OerOVyVfMlk/AYgBhFmEWYRZhlldb2UO6XBPp3BN17PMXD4oB179r233yPQ8PG0eVP+TDww0IKB643/Lcb8pp8K35Kt42CG2K2IEA7bsDdIqEwEkJINBnalglaj8wiUX6f27V/Xar7j/rVfOv4DU3j+hHYzt2MvmK2fIJdOKAFfQmZvj7Cx7w4MGVjwHuB4QGiSIIvQjd5IN+PvBMyh/y4eEGBFwshPdIuE3+JH/miAdvc4PYpojtCbi2pX23506JEDgjAQT6TK1qiToW55vvr5+1SK/z3A/FPiNxXivrdU4mVzF7AAIWAwiRCJGssOxMqplIM5F2+RFhmhXpigHigftBsRD2DzaOOsCYDxfzE1A8kC/IF6l8oX1rxYfiLX9kU8IeBGjfPahTJgTOSQCBPlO7WqKOBHrf0Uf7JMS7z9Rxs5XJV8yWT0Ax4OODFeMmxsGDiZUmUaEQo33EB/GhWCA+eJBDPiAf+Bgof8iHhxsQcLEQ5oRwm/6C/iJHPHibG8Q2RWxPwLUt7bs9d0qEwBkJINBnalVL1CNifCjMj22brUy+YrZ8AhYDrKBnBT0r6DuTaibSTKT9pIgHlzy4pH+kfxzpH20cVf6QDw83IKB4oP/gwd0WD/IVbxuENkXsQID23QE6RULgpAQQ6DM1rBK1H/iNiPRTjstWJlcxewACigEfLwhRCFEIUQhRI0KUJpvkC4QHxQIPsniQRT5gheMBhrubuahxtXIk9wf9pWIhV3/pY2yzCKegLQlYPtmyUMqCAAROSQCBPlOzWqIeEefHVs2Hx8xWJl8xWz4BiwGEWYRZhFlW0PPOdXtIl2sinXuijn3ema8YcP27tt0n3/PwsHFU+UM+PNyAgOKB+y3P/aacBt+ar+Jtg9CmiB0I0L47QKdICJyUAAJ9poa1RB0J9H6gEu2Lxfjwu9s2W5l8xWz5BBQDPn5YQW9iBjyYWGkSiLCFsEc+IB+QD3jwoRhI5QO/r/whHx5uQMDFQhgj4TbjCcYTOeLB29wgtiliewKubWnf7blTIgTOSACBPlOrWqIeEeNjIX7ou9nK5CtmyydgMcAKelbQs8KyM6lmIs1E2k+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7s6qFezvGk4m2D0KaIHQjQvjtAp0gInJQAAn2mhlWi9gO/EZF+ynHZyuQqZg9AQDHg4wUhCiEKIQohakSI0mSTfIHwoFjIKTyoDOKNeFMslBpvPkYPMObDxfwEXCyEOSvcLjV+S7+/8G/8L5jIP/nv671KsHyylwOUCwEInIYAAn2mprREPSLOD62Yj/ebrUy+YrZ8ArDMTZMAACAASURBVBYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaOKn/Ih4cbEFA8XPV+uHo+2Lr+ircNQpsidiBA++4AnSIhcFICCPSZGtYSdSTQ+4FgtC8U5FPHzVYmXzFbPgHFgI8PVtCbGAcPhElNstwn8UA8EA8I0YoB8gH5QLGg/sHHRPlDPjzcgICLhTBHhNuKlzh++E7/ohj4Jl78NRvENkVsT8C1Le27PXdKhMAZCSDQZ2pVS9QjYnwozI9tm61MvmK2fAIWA6ygZwU9QnRnUs1EmgcTflLEg0seXNI/0j+O9I82jip/yIeHGxBQPNB/8CBPonvO8aTibYPQpogdCNC+O0CnSAiclAACfaaGVaL2A78RkX7KcdnK5CpmD0BAMeDjBSEKIQohCiFqRIjSZJN8gfCgWMgpPKgM4o14UyyUGm8+Rg8w5sPF/ARcLIQ5K9wuNX5Lv7/wb/wvDMg/+e/rvUqwfLKXA5QLAQichgACfaamtEQ9Is6PrZoPj5mtTL5itnwCFgMIswizCLOdSTUTaVbQu/yIMDAuDMAHPoqBq94vNo4qf8iHhxsQUDxc9X64ej7Yuv6Ktw1CmyJ2IED77gCdIiFwUgII9Jka1hJ1JND7gWC0Lxbjw+9u22xl8hWz5RNQDPj4YQW9iXHwQJjUJMt9Eg/EA/GAEK0YIB+QDxQL6h98TJQ/5MPDDQi4WAhzRLiteInjh+/0L4qBb+LFX7NBbFPE9gRc29K+23OnRAickQACfaZWtUQ9IsbHQvzQd7OVyVfMlk/AYoAV9KygR4juTKqZSPNgwk+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7kSXTPOZ5UvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfuA3ItJPOS5bmVzF7AEIKAZ8vCBEIUQhRCFEjQhRmmySLxAeFAs5hQeVQbwRb4qFUuPNx+gBxny4mJ+Ai4UwZ4XbpcZv6fcX/o3/hQH5J/99vVcJlk/2coByIQCB0xBAoM/UlJaoR8T5oRXz8X6zlclXzJZPwGIAYRZhFmG2M6lmIs0KepcfEQbGhQH4wEcxcNX7xcZR5Q/58HADAoqHq94PV88HW9df8bZBaFPEDgRo3x2gUyQETkoAgT5Tw1qijgR6PxCM9oWCfOq42crkK2bLJ6AY8PHBCnoT4+CBMKlJlvskHogH4gEhWjFAPiAfKBbUP/iYKH/Ih4cbEHCxEOaIcFvxEscP3+lfFAPfxIu/ZoPYpojtCbi2pX23506JEDgjAQT6TK1qiXpEjA+F+bFts5XJV8yWT8BigBX0rKBHiO5MqplI82DCT4p4cMmDS/pH+seR/tHGUeUP+fBwAwKKB/oPHuRJdM85nlS8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStR+4Dci0k85LluZXMXsAQgoBny8IEQhRCFEIUSNCFGabJIvEB4UCzmFB5VBvBFvioVS483H6AHGfLiYn4CLhTBnhdulxm/p9xf+jf+FAfkn/329VwmWT/ZygHIhAIHTEECgz9SUlqhHxPmxVfPhMbOVyVfMlk/AYgBhFmEWYbYzqWYizQp6lx8RBsaFAfjARzFw1fvFxlHlD/nwcAMCioer3g9Xzwdb11/xtkFoU8QOBGjfHaBTJAROSgCBPlPDWqKOBHo/EPy/W/X681bdm9Ub/twft+rxq1nNkbjGX5fJV8yWT0Dx5OOAFfQmxsEDYVKTLPdJPBAPxANCtGKAfEA+UCyof/AxUf6QDw83IOBiIcwR4bbiJY4fvtO/KAa+iRd/zQaxTRHbE3BtS/tuz50SIXBGAgj0mVrVEnUktruV8c8fdRK/OVH+Z/1PYv39560KV8+7bbOVyVfMlk/AYoAV9KygR4juTKqZSPNgwk+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7kSXTPOZ5UvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfuAXiPTvPxvBvRHiw+OP5unr859WpO/YyeQrZssn0IkDhCiEKIQohKgRIUqTTd+/kC/IF+QL8gX5gsUu5Q91N/VQ42r6y3pVPOOF/A8qPONNo5zCtiJg+WSrAikHAhA4LQEE+kxNa4k6EOfD1fOvaL87JvH+/mcr0LOCPlMDHcysxRNCC0ILQgsr6HnnuonuOVe8Idwg3BBf5/kLHRtHHWz8h7t5CCge3KdyPff7ee53tWkp7at4yxPNWN2bAO27dwtQPgTOQwCBPlNbWqKOhHi//8etekf7nRBfNe+gv0WvuTFbmXzFbPkEFAPuU4NOJhJMJIgH7gfyAe/EVQyQD8gHigXGB+nxgb9Hyh/y4eEGBFwshDkz3Ob+Sd8/5Jdl4w3yzwY39k5FWD7ZqXyKhQAEzkMAgT5TW1qijoR4/xobBPpM1M9r1uKJFfSsoGcFfWdSzUSaibSf9PIqH3t4Cw+EeoS0vpBm46jzDhWp2QwCigfyJflyi3ypeJsRopx6IAK074EaC1chUDgBBPpMDaRE7Qd+gUivH4jVK27C46lX3HTsZPIVs+UT6MQBQhRCFA9qeFDDgxoe1PAXVdYX8KCOB3V+PP1hfOTPKX/Ih4cbENC4WuLslPjRueQb8s038UL+2eDG3qkIyyc7lU+xEIDAeQgg0GdqS0vUgTjvXmPz+ln/SWX8nvnqn1uV+pFY3kGfqYEOZtbiCWEWYRZhFmEWYRZh9oMQiZDUX0EtJl4kgZ/dQ1fhYeOog43/cDcPAcXDVeKf/Ff3CXu1t+ItTzRjdW8CtO/eLUD5EDgPAQT6TG1piToS6N1+CfG3H7fq8bP+p/Pdp38ffXCdjmVyFbMHIKAY8PGBsHA5YYGJ1b4TK/jD38UA+ZdXISgXEA/HvB/8PXyAMR8u5iegcbXuafI7+V2xkCu/k3/y39d7lWD5ZC8HKBcCEDgNAQT6TE1piToQ2kPh/fnzVt2bHyhy595/3Krnr744zwr6TA10MLMWT6ygZwU9QiFCKSvo7SFdrol07ok69lnhrhhw/bu23Sff8/CwcdTBxn+4m4eA4oH7Lc/9ppwG35qv4i1PNGN1bwK0794tQPkQOA8BBPpMbalE7QcmAyK9xPdQuI+3O3Yy+YrZ8gl04oAV9CZm+PsLHvDgwZWPAe4HhAaJIgi9CN3kg34+8EzKH/Lh4QYEXCyE90i4Tf4kf+aIB29zg9imiO0JuLalfbfnTokQOCMBBPpMrWqJekScj8X4oe9mK5OvmC2fgMUAQiRCJCssO5NqJtJMpP2kiAd1PKijf6R/HOkfbRxV/pAPDzcgoHig/+g/yOJB7/p/4aV42yC0KWIHArTvDtApEgInJYBAn6lhLVFHAr0fCEb7QmE+ddxsZfIVs+UTUAz4+ECIQohCiEKIGhGiNLkmXyA8KBZ4kMWDLPIBKxzLH+1u56HG1cqR3B/0l4qFXP2lj7HtQpySNiRg+WTDMikKAhA4JwEE+kztaol6RIwPhfmxbbOVyVfMlk/AYgBhFmEWYZYV9Lyz2h7S5ZpI556oY3/9FYpi6vpLbbtPvsNDceBjofwhHx5uQEDjavID+WGL/kLxtkFoU8QOBGjfHaBTJAROSgCBPlPDKlH7gd+ISD/luGxlchWzByCgGPDxwgp6E1/gwcRqi4mVyiDeiDfFgvskHogH4uFYD1r8PXuAMR8u5ifgYiHM4eE2+Z3+LUc8eJv5Q5sSdiDg2pb23QE8RULghAQQ6DM1qiXqEXF+bNV8eMxsZfIVs+UTsBhgBT0r6BEGO5NqJtJMpP2kiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+BB6xYPWhVvG4Q2RexAgPbdATpFQuCkBBDoMzWsJepIoPcDwWhfLMaH39222crkK2bLJ6AY8PGDEIUQhRCFEDUiRGmySb5AeFAs8CCLB1nkA1Y4lj/a3c5DjauVI7k/6C8VC7n6Sx9j24U4JW1IwPLJhmVSFAQgcE4CCPSZ2tUS9YgYHwvxQ9/NViZfMVs+AYsBhFmEWYRZVtDzjm17SJdrIp17oo79Y70ahfY6fnvZOKr8IR8ebkBA8eA+ub+Pf3+rDUttT8XbBqFNETsQoH13gE6REDgpAQT6TA2rRO0HCiMi/ZTjspXJVcwegIBiwMcLK+htMgUPJpaalLlP4oF4IB4QWhQD5APygWJB/YOPiQOM+XAxPwEXC2GOCLcVL3H88J3+RTHwTbz4a/KHNiXsQMC1Le27A3iKhMAJCSDQZ2pUS9Qj4vzQivl4v9nK5CtmyydgMcAKelbQI0R3JtVMpHkw4SdFPLjkwSX9I/3jSP9o46jyh3x4uAEBxQP9Bw/yJLrnHE8q3jYIbYrYgQDtuwN0ioTASQkg0GdqWEvUkUDvB4LRvlCQTx03W5l8xWz5BBQDPj4QohCiEKIQokaEKE02yRcID4qFnMKDyiDeiDfFQqnx5mO0/CEfHm5AwMVCmLPC7VLjt/T7C//G/8KA/LPBjb1TEZZPdiqfYiEAgfMQQKDP1JaWqEfE+FCYH9s2W5l8xWz5BCwGEGYRZhFmO5NqJtKsoHf5EWFgXBiAD3wUA1e9X2wcVf6QDw83IKB4uOr9cPV8sHX9FW8bhDZF7ECA9t0BOkVC4KQEEOgzNawStR/4jYj0U47LViZXMXsAAooBHy+soDcxDh4Ik5pkuU/igXggHhCiFQPkA/KBYkH9g4+JA4z5cDE/ARcLYY4ItxUvcfzwnf5FMfBNvPhr8oc2JexAwLUt7bsDeIqEwAkJINBnalRL1CPi/Niq+fCY2crkK2bLJ2AxwAp6VtAjRHcm1UykeTDhJ0U8uOTBJf0j/eNI/2jjqPKHfHi4AQHFA/0HD/IkuuccTyreNghtitiBAO27A3SKhMBJCSDQZ2pYS9SRQO8HguG+X/UT1/uft8qJ8r3jzT6/P5OvmC2fgOLJxwFCFEIUQhRC1IgQpckm+QLhQbGQU3hQGcQb8aZYKDXefIyWP+TDww0IuFgIc1a4XWr8ln5/4d/4XxiQfza4sXcqwvLJTuVTLAQgcB4CCPSZ2tISdSjGp7YjgT5cOa9ts5XJV8yWT8BiAGEWYRZhtjOpZiLNCnqXHxEGxoUB+MBHMXDV+8XGUeUP+fBwAwKKh6veD1fPB1vXX/G2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuBX0qYb/bpPK2glyivTx33djL5itnyCXTigBX0Jsb5+wIe8ODBFQ+ueHDFgyse1Fhf4MQn+sf+gzvG0uWPd7fyUOPqrYVayqsfll4xP5F/trq7ty/H8sn2RVMiBCBwMgII9Jka1BL1iDjvRXhW0GdqgXOZtXhCiESIRHhBeEKIRIjkwaTFgBc94AGPD+MjG0eda3hIbb4koHggf/QfZOkhAg/61nvQqXj7Mly5rHACtG/hDYR7EDgQAQT6TI1liToS6P1AMNwXCfS947yDPlMLHcus4snHB0IEQsQHIUKTK+KFiadigYn2ehNtMeX+4v5SLHB/HeP+8vdsacO/16O63e7V812aY+f2x8VCmMPDbe7nY9zPR8u/Reafc9/mm9XO8slmJVIQBCBwVgII9Jla1hJ1KMantiOBXq+2CT/NViZfMVs+AYsBhFkvzjseRxuY4y/vgFYMEL/cv4oF90k8EA/EQ/7+wcZRQ0M+L5TXoq0/9/6sNtHMEeiHWiTrfsUD+Zf8u0X+VbxlDWqM70aA9t0NPQVD4HQEEOgzNakStR/4pYT5Zp/O4x30mRriJGYVJz6eWEFv4jw8mFhtMbFSGcQb8aZYcJ/EA/FAPOQX1sV4jfvN20iMC9/Pu7+fH6/2oN8X7mgPrbuFQL8uz4nWXCyEMRVuk9/p33LEg7c5MT457VgEXNvSvsdqM7yFQKkEEOgztYwl6hFxnnfQZ4J/QrMWT6ygZwU9wmBnUs1Emom0nxTx4JIHl/SP9I8j/aONo3pjxFf1cOLKVivm4/IR6GMiC7837fnh4Yrigf6DB616CJhzPKl4WxjcXF4oAdq30IbBLQgckAACfaZGs0QdCfR+IBjui15x0zvOO+gztdCxzCqefHwgRCFEIUQhRI0IUZpski8QHhQLOYUHlUG8EW+KhVLjzcdob/g3TdDtXbbWDgT6tUg2dqa1p4uFMGeF26XGb+n3F/6N/0VROv+sHP6Y24WA5ZNdSqdQCEDgTAQQ6DO1piXqUIxPbUcCffjueW2brUy+YrZ8AhYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaO6g353tXzXou1HxZdV1XVnit7t9ujCt6M463Xr8xJ/PCrF+NvVaecQKB/PWo/ZLtznvxubOgc99k/L/Yz9vHTcVdYI3Q3QnaqnLqeznZkTw69n9V95Pq6Sp/LqXyd6zp0GXUZ61VFIZuhH+ANz9G94T7dfr6TLxUDa8WD4k23MZ/nIkD7nqs9qQ0E9iSAQJ+JvhK179hTwnyzT+fxDvpMDXESs4oTH0+soLfJEzyYSGoSxcQaYYF8QD4gHyCsKQZS+cDvS40LO0JyLGbrgkZIjl6FUwvGKaG4u89bGRToa2H+/mx/llZCtLRud70XoCeU768Nz3P1C75/Ol6JR1h443voYyiI26k67+7e69+yTHGaWk4t0MeM9FCgLaNuKVbQMx4qczw0mH+UYvg8LAHXtrTvYZsPxyFQFAEE+kzNYYl6RJznHfSZ4J/QrMUTK+hZQc8KL1a4scLPHtIhRJQpREgkpX1oHy9aFLCwwMZRg2NECb7NKvZA0HaX1AJzLAb7I7132NfC9TyBPhS+axfTDwR67jdienv9J4H60/HhusbCvgR6E+e9c+IYser5Ob0cCfTdcnyj+PFAd//n+jk3FQ+lxKdyJv6c80Gz4q13/7LjFARo31M0I5WAQBEEEOgzNYMl6kig9wOvcF/0ipvecd5Bn6mFjmVW8eTjo4CJLhOJepUi7XHOiRTxTXwjLCMsk9/Pl999m34c/klgDn84dlz0jcX7+QJ9QswffSgQVGJQ+L5Vt65ybRfV/g4dH65rXa9WeE/Xs+EXPeDQK3OmPEiIy6kF+gSjRN1VzlDdBcHFQniPh9vkf/J/jnjwNhWAfJ6KgGtb2vdUTUplILAbAQT6TOgtUYdifGo7Euj13vnw02xl8hWz5ROwGGAFPSvoWUHfmVQzkWYi7SdFPLi0vyqAx/mEZT00JN99n+9sHDVxyCcRu9a4h0VrZ25Lgb4Wr5tV/sH73Vvhu65g97xWVFf1h483dQ1si1392dqqbcTC+UyBfkI5OQV68iX5cov8qntI9x+f5yJA+56rPakNBPYkgECfib4StR/4pYT5Zp/O4x30mRriJGYVJz6eEKIQonhQw4MaHtTwoIZXHVlfgHD9vXAtceoK4wtfx6njws774ssQ6OsHAZEgnlxFHlSyOR6+Dz446l5s3/yQq4T38bqG164i0A+s8g/LySnQXyn+VVfy5T75clb+6dwAfCmdgGtb2rf0VsI/CByDAAJ9pnayRD0izoer5Me2zVYmXzFbPgGLAYRZhFmEWYRZhFmEWR7UWgz4STE84PFhfGTjqIlDvlh8jlfJt2YSgnZH3G/P1Kr1jiatH1UNfiC2viK2G39v7H4S6PXjsrdI2G/dqn981o4PrYAPLrCi3Q/BxnaHrq/9b1f6D53XLyenQE/+YAX9Fg8u5uafxF2w7a7BvLStG0cp7XDtexSw+AmBCxJAoM/U6JaoI4HeDwSjfaE4nzputjL5itnyCSgGfHwgRCBEfBAiNNkgXph4KhZYMbfPijn4179nQPwRfyX0R96HeMjnhSitHm8ONuJU5z3mWmneUdcbkfkWXV81YnrwHnaJ886HjgmVdbtVrXit1+aE4neqrKac8FrvZ+hPdN2n4w5Bsq5u973zXvv4IUZNb0h4jwX66eXME+iHyu82vGuHMCbDbfIV+SpHPHib3TBMf3u/qsfdPfxqXmV1v1eP1zt9bq69CPSzyKqtZl3EyRCAAAQSBBDoE1DW2GWJekSMD4X5sW2ztYZja9nwHXc4cVjLMHZSBCwGEGa9OO94IHwhfCkGiAfuB8UCwgrCCvmAfJDKBzaOSg2yApFc54VieXtJK4jrvFsgwrfnBeKzRDanyjfCd1+gd4K6hHS9Xz41xk6dU+8L/Q0fBtR+hoJ9I7TLL//ZPV7XI1HXjuOyE/s5JJAnBHpf0Ody5gn0MfvYv7p21n6MJxlPb7DwSfHWyRGpL69H88qpW3V/PKrHI/je+yublIGV9iHQzwI5uX1nWeVkCEDgigQQ6DO1uhK1+/wkvn86LltJV+NJxdBEIXnxgp0I9Avgzb9UMeDjaYOBpCa3lIfQoVhA+ET4JB+QD8gHPBhVDBwxH3if5w/BuOKEBFwshDEcbjPeYbyTIx68zQ/3UvJ3Jvwzp3vnL2w+mFl+GIF+FkPXtlPad5ZRToYABC5JAIE+U7Nbos64gl4rZMIFLfGfn2aqnvvb28R7J7OVdnnDFk+soGcFPe+g70yqmUgzkfaTIh5c2ipIePAgRSI6+bHNjzaOuvyIEgCOgOKBfEm+3CJfKt7G7z79hUzqL1rGr1z9KAL9LKTT2neWSU6GAAQuSgCBPlPDW6KOBHo/EIz2hSvoU8fNVsfX5k9Ct1ox3ym7QqCPeSz+3rRn+LQlsKkY8PGBEIUQxYMaHtTwoIYHNbyawfoChOhWiJbYxHihLzx6JsHYis3rEtC4mvul/qsg8kU/Xyg21upfPucfCfTR71QM3qbv6vVsX4HjY3roffWN4N6fZqrM6KFAINC/3Wt37u2rt+4P90Ku+L931T3PnX+vHsnX8vT9vt+f1atjcso57oJ39Xrc7bVAjsH9/qh6r+wP6u/9tFd8Be/3fz+rR1DPtO8dJ+2LZ+/GZPwHAQhAYCEBMslCgEOXW6IeEeNDYX5s22x1ChsXdDun5vjiO7r0ex1zFHd+m+PtaTGAMIswizCLMIswizDLg1qLAdc/ri2kYO98r/KxcdT5B5TUcAIBxQP5g/y5Rb5XvH0MzUZIduenhXBZkLB+q25OlPfvq2+Fandt579AoO7st9++SAv08tuJ3uH78Ds/oN28gsf7fH9Uz9erer1asTv8fQxXdv0aH1e/Z/Vy57qHDPeupjDlHCfOP72gfu/a8uJ71179l/81q5qtq0/7Q7x3bUf1jH3vsmu/iVO7hy0IQAAC3xFAoP+O28erlKjd5yfx/dNx2eoWqk5pylP29lzZut2ijtg616hDc4WmOvVAoFcnKtvxmMD7HQw4hs+L/Yx9/HTcO1s97Kl4/bQ/9qd+NZCzHdnTic2PeA37Oa2cmltdhy6jLmO9qkjl1Z/dc8JjWwwkVYYrV9vuk+/wIB7OJ1ypTbm/ub8VC+R7+rsz5gNfJz8o5X9XJ+BiIYzxcJv8R/7LEQ/e5oQbr7vCuxGyoyXrNnfU3NXsNgu+bt15ZHIu76/RXDiac9u8PbJTDdh/v6p35GOlczt/7d+U19lnzjcbU87Rj1QndBDN40M2A/Uxju6BSLjaXzZG/Wz9dm07tX3bq9iCAAQg0CeAQN9nssoeS9TZVtB7RT34k66oY7VaNB1p1MHUgnG30607qe4+b6bp1MJ+Th29q2fYoUmIDs/1dieU768Nz3OdY/D90/FKnWlYeON76GPYGdupOu/unqa3LFOcppaTZjQwENIgxhyyBvQbFk+soPcPDPwgiBWk9vAEHgirCKs8OFEMkA/IB4oFhMZWaLRxVHd4xbeLElA8kC/Jl1vkS8Xb9NstfsWLexWLrh6aS9bHNc8N576ak7Y2PtjSvDgUrZtLkvZlrvOZ8lP77tWz9x4aXTzjHP86m3f1fof/XvWragINQfXvMHHFpbQD74Z8aDUBeZf6nN++KSvsgwAEIFBVCPSZosASdSTQ+4FgtC9cQZ86braSvqoDqZ/c3sLOyP6MLNW59IX7usOdJ9D3OjoJzZEfPdebDrG9vvGnP3JoLv10XH8y169rLOxrYNEtShyj63t+Ti9Hg4FuOQN/kSBuvZPr6isGfHwgTCNM86CGBzX8RUtn9SNCZCtESmygv0B4Uixwf9T3h78negNSdlyRgMbVukfIl+RLxUKufPld/nFCvV7Fojlqfw7fuYcbcb3zGppmX3+aOTD/HRHoNb9t5/Aq3b2H/lk9/et2wlfiyO/mvPBd7+71PM/EO+0/ntMwiP5qXve1/wy1iMH6DOkLA1xU1ehT5Ua7+QoBCEBgNgEE+tnIpl1giXpEjA+F+bFtszVatDoS9361Z/PjLUOdTm2oXh3edprzBfqEmD/6UCCowKDwfas6A4rgktrfoePDda3r9ameDT9jp4Jru+0gZHo59QAmwShRd/szwP7IyTtiMYAwizCLMIswy6un7CFdrol07ok69vmLB8WA69+17T75noeHjaM0vOPz0gQUD9xvee435TT41nwVb9/edJoD19PEZi7am7M21vcQ6N0PyQ6K5e0cPKy/E/PDH2VNLNb3gn/6nJbBq7N6PlhJHxaGQB/SYBsCECiYAAJ9psZRR+wHJiMi/ZTjsjXF1WQHPiD6binQa9W66qLPVviua9c9r9+hDx9vOuoJg4PaRiyczxToJ5STQ6D38cIKehMz4MHESpNAhC2EPfIB+YB8wIMPxUAqH/h9UwbTnHN6Ai4WwhgJtxlPMJ7IEQ/e5pd3Vnd+r0V5/XmyM6+5cmeOPShQD9gaPL+138oLsuFewxO+iF77034KhXvnvmMztEDP16l3zjTbKmN41f/Qwrt59r3/7mE7/0EAAhBYSIBMshDg0OWWqEfE+bFV8+ExszVUWLi/6cA6T9jbHjQ8s/kV9bbTTAvXA69k8eXEIndtPhb+6+/RuclV5IF7zfHwffDB0fadcfa++KEOtnOV/5KuZ9MR91Yj1HbbQc70cnII9GMTTx1jYsHEwuUM4gGhSjFAPHA/KBboH+gfrpoPZo2l+0NH/qV0WQAAIABJREFU9pyMgOLhqveD+gTqv834QPE2ehu5ua9/p3p01ruZe9qcV69b7f4OnL/Kzo3m3T2Buy5DYn5vvq3z4x+b1StZO/sb/1Jz6Lt7ENZqDVHNmq9T5tb9c+R7O0cPrPtV9cH3pj79c/t266sQ6AN6bEIAAhsSQKDPBNs64kig9wOhaF8sxoff3bbZmuBrLD7HYnlrItEhNZ1XrOerA+zsn9zRJcpxTnwS6G0FQDTAaCvQrBDQ8SGBPbig2YwZ1buHrq/9bzv0ofP65eQQ6H38sILexGd4bDOxYCJXi/1njLfXH66P+Vf1/Bvh8oztq3sXYZ74Jr6bFdOJ4Rq7rkfA3Q/hPRFunzVfqq8/a/1K7+98jI3darY4zb2utn6H++Oh98/HYnwzv3Zx7N7j7t/7PnSuK1SCc2v77sXze1V/RiK6n+fr2M0/OHBl6DU27by4rpBW+N8fz+r1elXPZ3tuR6D3dbxXOu8VvObGdIYp5/hiWwbO3vP1qpy9Z8Os4+Nk3UINJF4RFx2OPi2fRPv5CgEIQGAuAQT6ucQmnm+JekSMj4X4oe9mKyzbdzRRp9F0Pp0/EVNnb72eMzLU6TQdXfAEXOK886FjQmXdugOG/mr5VFlBh6oXznk/w/pE13067qv1rAcOHUebP8UL9i0T6NuHCx3OeqAQlDNPoG/qG7APm9tigHfQe3He8Sh9II5/rGBXDBQbr3//2yZb8tV9Fusv+Y/8R3xyf37Z/9s4KhxcsX1ZAoqHS/R36uv/+C/548v8oTHSt/GiePt4w71fXmCWEO6uq1fVh6+OkZV38txn5zUzOtdNVF/V8x6I+M1q/eRiPj/PrxfBvTtiu/tR12FfVM/brX7dTd/2u3o97jb29OffH1XX5ynnqF4Tz210i45o7000mkQ4f/f7Ix1CxQ18qt4Dh9kNAQhAYDIBBPrJqOadqETtPoeEd62O/3RctnoeBCK5zul3PO6qVhDXee0PyUZWJeg3K0u8CN3s6/RdvmwnqKsD00p/rWgP7abOqfeF/oYPA2o/Q8G+feed1SH5J3OJunYcl53Yz8bHnkBe2wv9rGv2uZx5An0g/Hv2Xf/aOiNMa5CMkIiQ6u6LS8aDJtuD9f9v9Why+PvDX9zcbr9Xry+E7/d//uUn+vf//LI2uGx7fMGP/EX+4n7ZPn975uHwlO3LEnCxEN6D4XYx+Vl9/aCw3vT1v/27U5fY//ov5W7W18fHx76rry+Sz4fxjauX/pXgv/fhsnfcuSvu2pb2PXcbUzsIbEUAgT4TaUvUuVbQZ/Ibs2USsHhCCGIFKStIRyeiYxPNkiZq8uVbf/3qqj/+O3g/eIH+t39XTqD3k4Z4otpM/B9/DRyPz4++a9LuBPqk/ej8pfXl+rKEBtqD9lAMHOX+t3FUmcO8w3ilxTT9hSuHqYJ3VPFQdPz+XQvvt6avd/dc1996Rfyt6ev7x+vz3XjB9fVDx3UvDx13ZephfLf82B++D/Fx+/2xY90meDuRAO07ERSnQQACHwkg0H9E9N0Jlqgjgd53ztG+cAV96rjZ+s4VrjoBAcWAjw+Er6JWxHya2HAcIUsxsNr9q1V1K6ygl2/uczX/mhyFve1XCNOe5BvFAPdf//7zTE4wJtyzCmcT6Iu+X9TXL1xBT/9exviG/LNn5spbtmtb2jcvY6xD4CoEEOgztbQl6hExPhTmx7bNViZfMVs+AYsBhK+vVwBpEsZEpYyJCu2xTEhcvIKeB3086KM/oT+50IM5G0eVP+SLPGxeqRi9rjE6ia8zCSge3Gex45GVVtAXWz/yz8yo5fRSCSiflOoffkEAAschgECfqa2UqP3ALyHSv3/dqvuP+mmrzn382X9fvY55O5l8xWz5BDpxgLBmkyl/X8ADHlcTGrWqblBYGHsH/a/q9ce/Oj/Qdf/t9+r1d/Tg5q/f/Wog92fx7nzloGfzZ/JVc1x/9q4HX6///B7Z/re997a+X39VQ+d07+f61TnhD6W544+/Eu+8b3xxx99/dct/8I588sPV8gP19THfzSd1fvP7yh/yRR4i0EdAVvnqYiGMkXBb/dnuwrb6+i9X0A/19Z36Bf1n29fXfb6vf3C85ZHun/V7NrI/1NfreG2vHhOoPfznb0H5YT5rfNGr+drxwcD5zbXd8r5/1U/t7/fX+xhbJXoxUhoBxW9pfuEPBCBwPAII9JnazBJ1Spz/sx4UOoH++etWvX7dqkcj1t9HRPpMrmL2AAQsnsKBamEDz6UDV65ftqIaftfi990K+l/V87em//nj39Xrr/96sbzOL/+qnn8HE89gUu6O3//4vXr89q/KCfTueyjQ++//c0J++9BZtu/RRFvn3KPyVbaLY2dPft6a6x/RQ4U43t01Otdtfzo/vp7v17p/aO/rtbfPES53bfZfI6w3QrDPS6+g8Pezfph5f1bvzu57dbvdq+e7qvQ6Gflef9bH2ks+lONOfD2q2+1RueJfjzZPq5zWltt6V897eE59nZ3jbd2q/oL++DpnI7p2ti9W6uobIdNi88HXK+jV19fCtfXHTSzG/W3Loj5ffb3jomN6GO++h/24/+4ezLvxQfCgX+f4481YIx4PVP+rhX5fxm//qh5/1AsDJLzf4wcTGpc04wK3uMBda+cX/Js4vo6b5p/VbxkMjhCgfUfgcAgCEJhFYMuR6izHjn6yJepIoHf7q39u1fuf/mp5/6N+bgVg4hp/3dGh4P/XBBRPPg4Q5lkRyoOawRWSxU601/xTbq2q80L0735Sq4mt+wzFafcjsWKiPNL7sbjAns6VAH+7RcK97DUTZU3abaL94cfqvPA+9uO1//t/lX6ANpXv6n6yKwS0vt7sIYOEBT9x/1Ce6pwqT8dkj+/deIIHPBQDR7h/vI9fj8RmXCjxPVSxG2E7/HFVCfB2WnNdeE5Vjaygn1hOLdDXontrW4J6V0T3An740MCVEX5PCvSNj+F59jAgeqDQXO/a4pMvM4jPPtWVH8ZsuF1MvlffbA+q4/6++Wu43+ofk9W9qD5Ufb3VR/ZC4Vuit3sw3jykt/Ndfx8cr+1L/L/5H6FXmV1+jfD+YTwgP92P4Havb378Nh5/mC/Rink9yPhQnnzt1G/D8bSv4+xI5YIjEHBtS/seoaXwEQLlE0Cgz9RGlqgjsX3sXfPPZhX9K7rGbGXyFbPlE7AY2HAgufdAlvIRfhQDftArYXhNofvA95NWjCk3JD87wnQzqW5WnL3//lXpn7v24VbWh+cHAnySf++4Ju3RxLnTXjrnVj1Tr6rx7aEVdb9Hr8ap7wdN6NsHA+kVfnXstOXFf3qv2HKfyfoRb50HO/AiHysGjnq/OL+97xsM+epV6l3h2xXbE79ttbo7txHMI5F7TKCfXE5SVNfK+nA1/MjDAHFL2Bryw3wP65S43pse2q9yV/5UPBQdzxKem9gNfe5sR8J0/SDcvbqu7k/V17//boTv6HxnS31qikd8vP4LN/cXdbV95Ya2P1XfO208kOqf1dd3/AnGHSqzPq7y6hX1Otb6s3/+dn56X1eOY8yVQYD2LaMd8AICZyCAQJ+pFZWofWccCe4S6d176N3xx8/6nwSXUKDv2MnkK2bLJ9CJA4QjhKMDC8slTpzkk8/XR7i/tArO/UVW0t/UO+i1Iq3ud8KcEm7bivvBiXAz0R047oV+NxFtVvyZPQnhf/+7fhjQTFYf//mvrcKr+Te+RysCbaLdlNtZcad9CR61kFCL/YdpX+5vH9e019D9Xd+D8JnPxzPLPuQbFrnrFfORcK9V8D4nRqvNva9D9ob269U4QTle/E7YTqzYr8X2W3WzZf0RsJ6QPuyHu7In3s/wJSp51a8uFsJ7KNy2/ibZv254/6mv760w14PlVH/Z9v+qY+8z7F9H+k8/vkgdDx8cuFfT/CdeAV/792k84P8iLlwYEPH2fv/x37Y/aHxxDxO67TX+YL+U9vQ+rxrFGCuFgO6xUvzBDwhA4LgEEOgztZ0l6pQ4734gthkY6rzwMxTonZivY5lcxewBCFgMINy0A/VoIO8nEvCBj4Tgk8eH70PCiWtU3/7EtzuRb1fUBSvswvtncCLcCAMfjtvE/JZeQff+qyvUt39an17hZ/e3xIKm7pp4uxzZXwGoVXU3W42v883eReKF+u6/glJt4GJV2+6T79vwsHFU9jFfI1gPjvMD4bzxZVwUHxLAZ5QzUxTXq3dqZpG/JxPoi77/JIRH/V2bP9L9pfr//gr6pr+PxguOQb//bB9EDB13/XgdI26uGr16LhhPpMcD7YOE3oN8d636+jBfBuMOMajbT309K+izpzcKSBLQfZA8yE4IQAACMwgg0M+ANedUS9SRQO/261U2j1/d99BrPwL9HNLXOFfx5D41KGVij7BBPFz0ftCqusF8kJr4zlxhNjgRboTOT8cb4dHnrpEHCW9Nwm2F4PhEW3/23llBJxsJHqygR5hWn0m+vGi+DIRCHwPZh41DgvpAwY3gfb+7H4cNXzej84fsDe3XdcHnTIHerrTV/YFIfzKBvuj8oL7e+sc4n3cfvNd1UR868cH0SP/p7X067n43RucMPkiox+vxeOBT/+zO7zw4aMrp9P/+/p45vtnpweg2+cfuXjY2JOBj241B+Q8CEIDAQgJkkoUAhy63RB0J9G5FvF/Z8KP/Y7AP3kE/hPPy+y2egommJhXu0w/6mmN8hwfxcH4hav4K+vEfX638O+nbFXNavdafCDf31+BEObz/2gcFw/mqWQEYTexdDHcm5i6//d3aa1fc1+Ulz//fTKGC/Mpf4NCfnnY84XKE7xuzjyiH3iWfKrgR2f072tM/2mrvce+9cmZGOd8K9JVelxO8Hqcn0CdeY2NVTTxEWOCLmV1hQ/HgY6LU8fOXK+iTD7KD/u0d/RisY9Drb4PzPx2v/tf0zYMPEtzYou2/NR54/VHfkyrb5i/W10d/gReMO2Sjbj/19aygX+HWwMQXBFwc+lj84lougQAEIBASQKAPaay4rUTtk3Uk0r9+NgOS5vP5Z/eVN+EK+o6dFf3D1LEIdOKg1IkEwsZphY3uRChewcX3zfloVV1ixXjtSzsRjv903D8gdpPxP+o/TX/99e/q+Uc9Cfb9lfLL4ES4ae/4eCMkOLuvv/5bObvKW4+/6mvc9/vtX75sd477rj99d+e05bf+u3fZP/74vXoEPmoyb+c3vtj3QFj4tEJPbec+U9dznPtbMUB8HP/Bp2/DLYZ/Wnkeier+1THBvvrVNoH4nbxuRIhPnt+I6kE51VRR3NsLVsvrh2tvwb6EQF8l/Rh44DDVl8zt5GIhvKfD7WL6A/X1g8J301eG75T3/V/z4Lvp659Nf6u+3vWhVt+R/tPnvvi496keM6ivD/txf83E8UAo2jt/hvp6a49g3GH++/qygj7z7YL5DwRcPPqY/HAehyEAAQh8IoBA/4nQl8ctUUfivH4g9tmI8zrPve5Gwn0o0PMO+i8b4GSXKU78wBchqZ1YBEKc2NhAvjnGd4RHP2g+WTx8s4K+vkfqiWz8OyjPv37Z67M8r8GJcBNPveO/qtcf/+r+vspvv1fObsu/Pkf5zH/+NrTi7Zd/cBD6ee/Za4V/Z6sn3LOCnhXx9JfB/dfeL1fsL5V3thseNqvHG+HGl98TzW/V/fnuuKT3v4enmgDubQWCvr/yQznunBmiuMoXr1sozputkVfxhPX1fxnQqd4sX6IrV/3a1q/gB09frqBXX+/65LCet4H+1p3T7z/bfBEfH+rr2/H2lPFAa989OEj19a29+tzwL/uUw5xvlfX1Q+OJ5vod+wO1w6pBjLFiCNC+xTQFjkDg8AQQ6DM1oSXqSKD3A4lon0R7ifHhd+3z12Xy9QpmNeGIJ0JHqbviycfByYRGDbJ7A/EdB9LyCd4FT1yJD4S3wb8gaCf+upfJLzyoI5+Tz30MHGXgh59ZCbhYCHNCuE1/QX+RIx68zaxRjfG9CLi2pX33ok+5EDgXAQT6TO1piXpEjI+F+KHvZiuTr1cwexaBXmKTHwQg1HdX/MIDHk0McH8gxClXIrQgtJAPyAfKAz4WrjDopY4fCbhY0D/6i/1XmKsNzpqvLdY+RiYnHHHOTvsStxCAwFoEEOjXIhnZUaL2A40RkX7KcdmKiij8a+KHoQr3uGT3FAM+XhCiEaIRonl1B39B0Fn9KAFOk3y+I8zTXyLMx/nAx0TJgz1824yAxtWKEfIF+UKxkGv8UEb+aebnqddPbXb3jReEQD/Oh6MQgMC5CSDQZ2pfG/iNiPNDK+bj/WYrk695zCLQr8nVYgBhFmEWYRZhlle72EO6XBPp3BN17LNiUzHgRRsevNs9nYuHjaPWHJxh67AEFA+54o37m1fNuRhQfCne9r9hyhfo92c034Ny2ne+71wBAQiURQCBPlN7WKKOBHrfUUf7QkE+ddxsZfK1a7bpuIM//Uz+UFX05L1+2l3/cJWefMvv+vPzj1p1ynFO+R+1elQvv9n+KertFttyJ7+r5z08p77O6uZtpX7UKr7O2Yiune2LlbraRshSg/5w4Kd97jxtc7wdGIsJfIgPxQL3B/cH+YB8QD641oMSf8+vNjLD0JEJuFgI+4Bwm/EB44Mc8eBt7n7TINDnaALXtmW0b47aYRMCENiSAAJ9JtqWqEfE+FCYH9s2W5l8NbPvZ3V3HUyolDfCdvjjqhLg7bTmuvCcqhpZQT+xnFqgrzu81rYE9a6I/nrcqlv40MCVEX5PCvTpQYq3FT8EaK53bfHJF+O54obFACvoWUEfrMiRuOTiQ9tMLJlYEg/cD+SDawnPtPfn9rZx1IpjM0wdl4Digf6S/nKL/Kl4m37HvKvX417Pyxvx935/VK93ZCGY375fj+D8e/V4dk+u57f1vFr++E+b0Ee23dcx+3Lm/awetkiuX25t9V15/+w858fAuU2Z7XzbWXhXr2dYv5uf57tFfN3/+ufd7vfqIV/Dk8fqFrELL0tti2fqGPsgAAEIzCGAQD+H1oxzlajd5yfx/dNx2ZpR/Fen1h13V/h2hnrit61Wd+c2gnkohvvShwX6yeUEHWenQr39w2XZdb1rmnqlVsvr4UJYp8T1dTUf/on52NjGfFiwoRjw8cSfwpsYDQ8mVltMrFQG8Ua8KRbcJ/FAPBAPn4VxMSrhfvE+LBiLcel5CLhYCGMy3Ca/07/liAdvc9ItpMVo9+r+eFav1ysQp6O/Im/mp06EdvadiP8IhP2OyP1+Va9Xsxjv/qiezq7719Xxux7G9h+1fVeWL+9Rl3vz5bYCeqdcJ68/W//qcltRPz5XDwXC/Xq40OFxj1hIk3C+OVG+8dUvPnRs4sl6XLcxdl0qvW/i0TvADghAAAIzCSDQzwQ29XRL1IdZQT8sctedaiTcaxW876DjDtJRGrI3tF+dd1CO7zgTthMr9tVxd1b/h43VdMJt3zzsh/fercgPxfsZvoTFrrVt8cQKelbQIwx2JtVMpJlIu/woEZB4IB6IB+6HVD6wcdRaAzPsHJqA4oF8Qb5I5QvtWys+FG9TbhqJ2e2ctblKc+/wgETm+C+/dW642Mybaea/vf0Dng3Yl4+uXqGQXg2V+35V796DgAFfmjJbu0OLAbs+m08hn7DOMaOBug3WoVtc59uc9u1cyBcIQAACEQEE+gjIWl8tUUcCvdv/acV8fNxsreVc0k7TSTZPxFVm+xkI583146L4kAA+oxzfcU4T6J1L1jH7OkT+Np1w22cP+VdXrrfKf6YvScQLdrbtwEBag2b36bjw/VgrGGkv2ksxwP1L/lIsuE/igXjIHQ8+xhaMxbj0PARcLIQ5J9wmH5GPc8SDt/nxFpIY7V5n867enX+v+lUyobjezG9bMVsFaBV+NB/WArrQhi5JfQ7ZlxDfTqybq4fKTRkfOLdXps67V8/B5f46J65vXa40gg6nXjnycdyWzgo/XdtOa9/wKrYhAAEI9Akg0PeZrLLHEnUk0Mfi+5TvZmsVz4aMjAvWvavUqTV/UtfrnzUA6B2YUY4vY7pAbz5q0NBbAR/+SOy4H6UK9Jq8+kEAr7oxcR4eCDu6N5hYM7EmH5APyAc8CFQMKB+4T79tg0U2rkxA8aD4iOOF73UOgc86/ani7fM918xPm3yl6zqfobiu+XjvnelDInNjP7Qx5tSg/aF59FC5rhD3Hvpn9fSvnnGvytErcSJRPVVm+J579/qap3vJbvjfh3o1Njt/aZ8qx5scq0NYZrut9mn3sAUBCEDgOwII9N9x+3iVErX7HBPhpxyXrY+FLjqh6YwmddhhJzjUiX3ouKeU4zvOLwR6W00fXNt0wuHzgp4Ib/wSvi/wxcwu2FAM+HhBmEeY51VHPga4H9aZOCJEIES4GOB+4n5SLjhrPPgYXzAW49LzEHCxEOa8cPus8X/2+7v0+k3LP+0cu7+CvllRH96Gs0Xm1n5X4A6NBtuD9hNzZX/ZgC7Q+QHb+t7TPdh5payzMVhm5QX+8Adp2+cSH+rV2ESgD9qWTQhAoEgCCPSZmkWdzpg4P/WY2crkq5nVyvNQxZbYHeyrhe1A/E5eNyL4J89vXlETlFN30EE5crS53v5MzX8Pn74nBgdNxxyat3fMdXdWT/8L86E9DRYm+CIfV/60GECYRZhFSOtMqplII6y6/Fj6xBz/WNGtGCBe97lfbRy18vgMc8ckoHjgftznfrxaPlS8fb5bEnPYsYsGxewhOx+E7LisQftzBHr5cq8enVfUaH9qzh292z7y690T3AdsNdfxipsIIF8hAIFiCSDQZ2oa64ijV9z4gWC0LxTqU8fNViZfu2abDjf807pQwB7oqNXxhaeaAO5txeL2h3KcU76s+Dr/xKByv8huAr0eIoQ+h6+3MVvhK25U64QfqdX9M3yR5TU/FQM+PlhBb2IcPJhYaZLnPokH4oF4QAhXDJAPyAeKBfUPPibWHJxh67AEXCyEOSLcVrzE8cN3+hfFwDfx4q+ZcMdoTh3Oc+0y/056+zay2nxIsB7aH9gMNwfm/dXgq2xT9pu5dm9+3bxTf2DOnqy/+dbYDISHegFhVx/wp7811480hcG6pepgBSc3XNtObd+kAXZCAAIQaAgg0GcKBUvUI2J8KMyPbZutTL5itnwCFgOsoGcFPUJ0Z1LNRJoHE35SxINLHlzSP9I/jvSPNo4qf8h3Lg8bESzQ0Yqon+KB/oMHeRLdc44nFW/Tgl+C8q26P57V8/WqXv7d7Xc//u0I11+IzBKyb3f3Hvh7dR+7OQft9wXyum5pcVtluvq8Xq/q+dT7552w/WEFvf9Leednfa1jodfcdF1vud3ce+r9u+5rZo5/h5tzdrBu6TqMtd289h2zxDEIQODqBBDoM0WAErX7/CS+fzouW5lcxewBCCgGfDwhRCFEIUQhRI0IUZpski8QHhQLOYUHlUG8EW+KhVLjzcfoAcZ853FxSMTbv4YuFsKcFW6XGr+l31/4N/4XBvPyz7t6OfE8/Ovw+6N6dl4R863IrJXr9T3QE67D23NQxB66t4fE7Xf1fLRi+e1Wv+6mFu4/CPTVRBbe77qckNs9xc2dO1i3oTqEYLrblk+6u/kGAQhAYDYBBPrZyKZdYImaFfTTgHHWKAGLJ4RZhFmE2c6kmok0K+j9pJcHlzy4pH+kfxzpH20cNTra4mBLYEiAa8/4tOVf1dF7rcWnq7Y5rnig/+DB4hYPFhRv20Q3pWxNgPbdmjjlQeC8BBDoM7WtJepIoPcDwWhfuII+ddxsZfIVs+UTUAz4+ECIQohCiEKIGhGiNNkkXyA8KBZ4kMWDLPIB7wieN9pdLtDPK2/bszWuVo7k/qC/VCzk6i99jG0b5pS2EQHLJxuVRzEQgMB5CSDQZ2pbS9QjYnwozI9tm61MvmK2fAIWAwizCLMIs6ygd69O40GdMXD5ER7jf1oPH/goBq56v9g4qqghXyOCB6+x6LxT2b97+VbdolXo9Y9IRj94qB9tHLLl6u1f6VC/TkLvhK65dG3pRyrFLD6nPu7sBP53HA/2N/50DhfQBmHddG+4T7ef7+RLxcBa8aB4KyD0cSEDAdo3A1RMQuCiBBDoMzW8ErXv2EdE+inHZSuTq5g9AAHFgI8XhDmbPMGDiaQmUUysERbIB+QD8gHCmmIglQ/8vlLGfBLfQ+U68U5kieV2WnNd573RE23pncuOQ3v90PuWh1fQyydnx/wS16m+6PydPp3vPh5Y+OLH1CELxlN5xlOe8U7xTrF5CVg+yVsM1iEAgQsQQKDP1MiWqGNx/lc9IHz8ulXvX7fOj788/kz/oKzZyuQrZssnYDHARIKJBCu8OpNqJpJ5JpISueALX9f/EA8I34qBo8aDjaMKGfIlfxzRL3KPV8yHAnqzHa2on2yreQDQE9WT+z8L9K3I30Kd7Et7yS5bioejxvPR78er+a942yXYKTQ7Ado3O2IKgMBlCCDQZ2pqS9SRQK/9tx/NL6f/uFWPn12hPn7dja7J5CpmD0BAMeA+Nah1n3yHB/GAcKYYIB+QDxQL9A/0j+SDfj7wTIoY830Sv+vX0JirWpXuV313X0dT6TUzPdW9qtpX0TSWvBAfX1+5E/2Coa7g/snHhJ05vljl9tlwsRDeI+E2+ZP8mSMevM19wp1SMxNwbUv7ZoaMeQhchAACfaaGtkQdCfRVs4LeHX/+E6yY/6cR6X/cqnd0jdnK5CtmyydgMcAKelbQ82CmM6lmIs1E2uVHhGkeVCkGiAfuB8VC2D/YOKqIIV8jfjeijnxrPyOBXivr3fk9IX6Gra0E+hn12qs5WtbcL6n7RfscJ22H95P2cXwaH8XbXvFOuXkJ0L55+WIdAlcigECfqbWVqP3AJRTcG4H+3rzOJjz+bFbVv4LzO3Yy+YrZ8gl04oB30Ntkwd8/8IAHD658DHA/TJsoIyzUYj7xQrzoXriK8OZjvogh3/Dq9KRw7aX/AAAgAElEQVR7zSto7ve7f0Dd1ehn2NpKoO86mKzS3jtdLIQ5MNy+yv1wtft/7/qWk3/2vvvOV77lk/NVjRpBAAIbE0CgzwTcEnUgtvtX10QCffg6m5RA746brUy+YrZ8AhYDCJEIkayg70yqmUizgt7lx70n3pTPCn7FAPFY5v1o46gihnzpd8mnXWsEeP/e+fB99Dp7hq3sAv0MX+T+Tp+KB+7XMu/Xs+VTxdtO4U6xmQnQvpkBYx4CFyKAQJ+psS1RRwK99msFPQJ9pgY4mVnFjfvUoNV98h0exAPCoGKAfEA+UCzQP9A/kg/6+cAzKWV8qPfKR6vN/Xvjg331j64G73tPXZfa518tf+++EmeWQD8sttfvtg98CplO9SW8ZodtFwvhPRJukz/JnzniwdvcIdYpMj8B17a0b37OlACBKxBAoM/UypaoI4Fe76BHoM8E/qRmLZ5YQc8Keh7MdCbVTKSZSPtJEa+6soe38OgLszy44EGmjaOKGicm3h8fiPOVXm3zfHe8rgXyWxWeaj8WG77/vXtCVdtLCOuNqN79kdj2x2Nrdu11owK99/RDvTq12eeL4oF8Sb7con9QvO0T7ZSamwDtm5sw9iFwHQII9JnaWonaD/xCkT56xU14PPWKm46dTL5itnwCnThAiEKI4kEND2p4UMODGv6iyvoCHtTxoM6Ppz+Mj/w55Q/58HADAhpXS5ydEj86l3xDvvkmXsg/G9zYOxVh+WSn8ikWAhA4DwEE+kxtaYk6FOfddiTQ84qbTA1wMrMWTwizCLMIswizCLMIsx+ESIQkVowrBrwoRLz4fsOzONn4kOp8R0Djau4PVtArV+Z88KJ4+y5auap0ArRv6S2EfxA4DgEE+kxtZYk6Eui1n1fcZAJ/UrOKG/e5xUBSZVAevBULOScuKoN4I94UC8QbKxTJB+SDtfOBj6mTjhOp1jwCLhbCHBNu0//Q/+SIB29zXphy9kEIuLalfQ/SWLgJgcIJINBnaiBL1JFAH66Yn7pttjL5itnyCVgMsIKeFfSsoO9MqplIM5H2kyJWCNvDW3ggbK8tbJ/Bno2jyh/y4eEGBBQP5Evy5Rb5TfG2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuB34hIP+W4bGVyFbMHIKAY8PGCEIUQxYMaHtTwoIYHNfxFlfUFPKjjQd2U8ZE/5wBjPlzMT0DjaomzU+JH55JvyDffxAv5J/99vVcJlk/2coByIQCB0xBAoM/UlJaoR8R5VtBngn9CsxZPCLMIswizCLMIswizPKi1GPCiBzzg8WF8ZOOoE44RqdJ8AooH8gcr6Ld48KJ4mx+pXHEEArTvEVoJHyFwDAII9JnayRJ1JND7gWC0LxTqU8fNViZfMVs+AcWAjw+ECISID0KEJhvECxNPxQIr/ljxRz4gH1w9H/h7oPwhHx5uQMDFQpgTw236S/rLHPHgbW4Q2xSxPQHXtrTv9twpEQJnJIBAn6lVLVGPiPGhMD+2bbYy+YrZ8glYDCDMenHeD4J4UMGDCu4H7gf+oqQjMiEsISzRP6YfxNg4qvwhHx5uQEDxwP2Svl/0MA8+6/BRvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfmAzItJPOS5bmVzF7AEIKAZ8vCBMI0wjTCNMI0wjTPOqI+sLeDDBg4kp4yN/zgHGfLiYn4DG1QjR/4/x1EbjKfJP/vt6rxIsn+zlAOVCAAKnIYBAn6kpLVGPiPNjq+bDY2Yrk6+YLZ+AxQDCLBOJjSYSmrQifCF8ufxDPNQiBvcD9wP3wzHzgY2jyh/y4eEGBBQP3M/HvJ81JjlK+yneNghtitiBAO27A3SKhMBJCSDQZ2pYS9SRQO8HEtG+WIwPv7tts5XJV8yWT0Ax4OOHFfQmFsKDiZUmaQinCKfkA/IB+YAHSYqBVD7w+8of8uHhBgRcLIQxEm4znmA8kSMevM0NYpsitifg2pb23Z47JULgjAQQ6DO1qiXqETE+FuKHvputTL5itnwCFgOsoGcFPSvoO5NqJtJMpP2kiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+DBrh7q5RxPKt42CG2K2IEA7bsDdIqEwEkJINBnalglaj/wGxHppxyXrUyuYvYABBQDPl4QohCiEKIQokaEKE02yRcID4qFnMKDyiDeiDfFQqnx5mP0AGM+XMxPwMVCmLPC7VLjt/T7C//G/4KJ/JP/vt6rBMsnezlAuRCAwGkIINBnakpL1CPi/NCK+Xi/2crkK2bLJ2AxgDCLMIsw25lUM5FmBb3LjwgD48IAfOCjGLjq/WLjqPKHfHi4AQHFw1Xvh6vng63rr3jbILQpYgcCtO8O0CkSAiclgECfqWEtUUcCvR8IRvtCQT513Gxl8hWz5RNQDPj4YAW9iXHwQJjUJMt9Eg/EA/GAEK0YIB+QDxQL6h98TJQ/5MPDDQi4WAhzRLiteInjh+/0L4qBb+LFX7NBbFPE9gRc29K+23OnRAickQACfaZWtUQ9IsaHwvzYttnK5CtmyydgMcAKelbQI0R3JtVMpHkw4SdFPLjkwSX9I/3jSP9o46jyh3x4uAEBxQP9Bw/yJLrnHE8q3jYIbYrYgQDtuwN0ioTASQkg0GdqWCVqP/AbEemnHJetTK5i9gAEFAM+XhCiEKIQohCiRoQoTTbJFwgPioWcwoPKIN6IN8VCqfHmY/QAYz5czE/AxUKYs8LtUuO39PsL/8b/woD8k/++3qsEyyd7OUC5EIDAaQgg0GdqSkvUI+L82Kr58JjZyuQrZssnYDGAMIswizDbmVQzkWYFvcuPCAPjwgB84KMYuOr9YuOo8od8eLgBAcXDVe+Hq+eDreuveNsgtCliBwK07w7QKRICJyWAQJ+pYS1RRwK9HwhG+2IxPvzuts1WJl8xWz4BxYCPH1bQmxgHD4RJTbLcJ/FAPBAPCNGKAfIB+UCxoP7Bx0T5Qz483ICAi4UwR4Tbipc4fvhO/6IY+CZe/DUbxDZFbE/AtS3tuz13SoTAGQkg0GdqVUvUI2K8E98fLqH/uFXvkfPMViZfMVs+AYsBVtCzgh4hujOpZiLNgwk/KeLBJQ8u6R/pH0f6RxtHlT/kw8MNCCge6D94kCfRPed4UvG2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuB3yfxfUSg79jJ5CtmyyfQiQOEKIQohCiEqBEhSpNN3/+QL8gX5AvyBfnCP9j1ObH8IR8ebkBA42r6y3pVPOOF/A8qyD8b3Ng7FWH5ZKfyKRYCEDgPAQT6TG1piXpEnGcFfSb4JzRr8YTQgtCC0MIKet65bqJ7zhVvCDcIN8TXef5Cx8ZRJxwjUqX5BBQP7lO5nvv9PPe72rSU9lW8zY9UrjgCAdr3CK2EjxA4BgEE+kztZIk6Euj9QOH/btXrZ/tueZ2rT95Bn6lRDmxWseHjhxWxNpmCBxNLTcKYWDOxJh+QD8gHvCNaMZDKB37fgceCuL4eARcLYYyE24wnGE/kiAdvc70QxlJBBFzb0r4FNQiuQODABBDoMzWeJepIoDfx/Z9b9fp1q+7NO+ifv+rvr39ulZ3TXGu2MvmK2fIJWAywgp4V9Kyg70yqmUgzkfaTIh5c8uCS/pH+caR/tHFU+UM+PNyAgOKB/oMHu3qol3M8qXjbILQpYgcCtO8O0CkSAiclgECfqWGVqP3Ab0ik/79mFT3voM/UCucx24knhCiEKIQohKgRIUqTTd//kC/IF+QL8gX5wj/Y9TnxPENDarKAgMbV9Je8yiynMB/GF/lnwQ1b+KWWTwr3E/cgAIHyCSDQZ2ojS9Qj4jzvoM8E/4RmLZ4QWhBaEFpYQc87c01032pirUk25fEXG15k4cGX3YNH4WHjqBOOEanSfAKKh6PEr/og/D3min/F2/xI5YojEKB9j9BK+AiBYxBAoM/UTpaoI4HeD6yCfY/mFTfvZl983In4ZiuTr5gtn4BiwMcHwsDhhAEmVqzQQthF2CV/H1NYIX+fJ3/7e7D8IR8ebkBA42ru7/Pc32rLUsdb5J8NbuydirB8slP5FAsBCJyHAAJ9pra0RB2I8fG75VlBnwn+Cc1aPLGCnhX0rKBnBT0r6O0hXakT8dKFAvyrRSni5zoPzmwcdcIxIlWaT0Dx4D7Jh+RDxUCueFC8zY9UrjgCAdr3CK2EjxA4BgEE+kztpETtO/oRkd6fxzvoM7XCecx24okV9DaZ8vcXPODBgysfA9wPCC0SGRCeryM8q825/z/f/57ReYaG1GQBARcL4T0TbpM/yZ854sHbXBCzXFouAde2tG+57YNnEDgSAQT6TK1liXpEnHcr6J8/6oT+GjnPbGXyFbPlE7AYQIhEiGQFfWdSzUSaibSfFPGgjgd19I/0jyP9o42jyh/y4eEGBBQP9B+fH2zpISDjre/HW4q3DUKbInYgQPvuAJ0iIXBSAgj0mRrWEnUkvPuBYLDv9bN5x/yPW/VotuNX4ZitTL5itnwCigEfPwhRCFEIUQhRI0KUJtPkC4QHxQLCyvfCihhyPx3/fvJtWP6QDw83IOBiIbynw23yJfkyRzx4mxvENkVsT8C1Le27PXdKhMAZCSDQZ2pVS9SBGB8L7/r+aFbRu2vuf94q7den2crkK2bLJ2AxgDCLMIsw25lUM5FmIu3yo0RU4oF4IB64H1L5wMZR5Q/58HADAooH8gX5IpUvtG+t+FC8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStS+Yx8R6accl61MrmL2AAQUAz5eWEFvYhw8mFhpEuU+iQfigXjgx/4UA+QD8oFiQf2Dj4kDjPlwMT8BFwthjgi3FS9x/PCd/kUx8E28+GvyhzYl7EDAtS3tuwN4ioTACQkg0GdqVEvUI+K8Vsh/+jRbmXzFbPkELAZYQc8KeoTozqSaiTQPJvykiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+BBnkT3nONJxdsGoU0ROxCgfXeATpEQOCkBBPpMDWuJOhLo/UAw2hcK9KnjZiuTr5gtn4BiwMcHQhRCFEIUQtSIEKXJJvkC4UGxkFN4UBnEG/GmWCg13nyMlj/kw8MNCLhYCHNWuF1q/JZ+f+Hf+F8YkH82uLF3KsLyyU7lUywEIHAeAgj0mdrSEvWIGB8K82PbZiuTr5gtn4DFAMIswizCbGdSzUSaFfQuPyIMjAsD8IGPYuCq94uNo8of8uHhBgQUD1e9H66eD7auv+Jtg9CmiB0I0L47QKdICJyUAAJ9poZVovYDvxGRfspx2crkKmYPQEAx4OOFFfQmxsEDYVKTLPdJPBAPxANCtGKAfEA+UCyof/AxcYAxHy7mJ+BiIcwR4bbiJY4fvtO/KAa+iRd/Tf7QpoQdCLi2pX13AE+REDghAQT6TI1qiXpEnB9bNR8eM1uZfMVs+QQsBlhBzwp6hOjOpJqJNA8m/KSIB5c8uKR/pH8c6R9tHFX+kA8PNyCgeKD/4EGeRPec40nF2wahTRE7EKB9d4BOkRA4KQEE+kwNa4k6Euj9QDDaF4vx4Xe3bbYy+YrZ8gkoBnz8IEQhRCFEIUSNCFGabJIvEB4UCzmFB5VBvBFvioVS483HaPlDPjzcgICLhTBnhdulxm/p9xf+jf+FAflngxt7pyIsn+xUPsVCAALnIYBAn6ktLVGPiPGxED/03Wxl8hWz5ROwGECYRZhFmO1MqplIs4Le5UeEgXFhAD7wUQxc9X6xcVT5Qz483ICA4uGq98PV88HW9Ve8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStR+4Dci0k85LluZXMXsAQgoBny8sILexDh4IExqkuU+iQfigXhAiFYMkA/IB4oF9Q8+Jg4w5sPF/ARcLIQ5ItxWvMTxw3f6F8XAN/Hir8kf2pSwAwHXtrTvDuApEgInJIBAn6lRLVGPiPNDK+bj/WYrk6+YLZ+AxQAr6FlBjxDdmVQzkebBhJ8U8eCSB5f0j/SPI/2jjaPKH/Lh4QYEFA/0HzzIk+ieczypeNsgtCliBwK07w7QKRICJyWAQJ+pYS1RRwK9HwhG+0JBPnXcbGXyFbPlE1AM+PhAiEKIQohCiBoRojTZJF8gPCgWcgoPKoN4I94UC6XGm4/R8od8eLgBARcLYc4Kt0uN39LvL/wb/wsD8s8GN/ZORVg+2al8ioUABM5DAIE+U1taoh4R40NhfmzbbGXyFbPlE7AYQJhFmEWY7UyqmUizgt7lR4SBcWEAPvBRDFz1frFxVPlDPjzcgIDi4ar3w9Xzwdb1V7xtENoUsQMB2ncH6BQJgZMSQKDP1LBK1H7gNyLSTzkuW5lcxewBCCgGfLywgt7EOHggTGqS5T6JB+KBeECIVgyQD8gHigX1Dz4mDjDmw8X8BFwshDki3Fa8xPHDd/oXxcA38eKvyR/alLADAde2tO8O4CkSAickgECfqVEtUY+I82Or5sNjZiuTr5gtn4DFACvoWUGPEN2ZVDOR5sGEnxTx4JIHl/SP9I8j/aONo8of8uHhBgQUD/QfPMiT6J5zPKl42yC0KWIHArTvDtApEgInJYBAn6lhLVFHAr0fCEb7YjE+/O62zVYmXzFbPgHFgI8fhCiEKIQohKgRIUqTTfIFwoNiIafwoDKIN+JNsVBqvPkYLX/Ih4cbEHCxEOascLvU+C39/sK/8b8wIP9scGPvVITlk53Kp1gIQOA8BBDoM7WlJeoRMT4W4oe+m61MvmK2fAIWAwizCLMIs51JNRNpVtC7/IgwMC4MwAc+ioGr3i82jip/yIeHGxBQPFz1frh6Pti6/oq3DUKbInYgQPvuAJ0iIXBSAgj0mRpWidoP/EZE+inHZSuTq5g9AAHFgI8XVtCbGAcPhElNstwn8UA8EA8I0YoB8gH5QLGg/sHHxAHGfLiYn4CLhTBHhNuKlzh++E7/ohj4Jl78NflDmxJ2IODalvbdATxFQuCEBBDoMzWqJeoRcX5oxXy832xl8hWz5ROwGGAFPSvoEaI7k2om0jyY8JMiHlzy4JL+kf5xpH+0cVT5Qz483ICA4oH+gwd5Et1zjicVbxuENkXsQID23QE6RULgpAQQ6DM1rCXqSKD3A8FoXyjIp46brUy+YrZ8AooBHx8IUQhRCFEIUSNClCab5AuEB8VCTuFBZRBvxJtiodR48zFa/pAPDzcg4GIhzFnhdqnxW/r9hX/jf2FA/tngxt6pCMsnO5VPsRCAwHkIINBnaktL1CNifCjMj22brUy+YrZ8AhYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaOKn/Ih4cbEFA8XPV+uHo+2Lr+ircNQpsidiBA++4AnSIhcFICCPSZGlaJ2g/8RkT6KcdlK5OrmD0AAcWAjxdW0JsYBw+ESU2y3CfxQDwQDwjRigHyAflAsaD+wcfEAcZ8uJifgIuFMEeE24qXOH74Tv+iGPgmXvw1+UObEnYg4NqW9t0BPEVC4IQEbkoofNaJFQ5wIAaIgb1iYMnAX9e6T+c/35lIKgaIh/z3w145g3Lpr4gBYoAYWBYD6ivnjJ9gvow5/OBHDBADR4uBE2rBVKlAAgj0zRPPoyUI/KVTIwbOGQPfTBR1jYsJbc+ZaOoaroefYoH4mf6gi1x8zlxMu9KuxMD5Y0B93jfjH+Lj/PFBG9PGxAAxoBgoUMvFpRMS4BU3J2xUqgQBCByLAB3/sdoLbyEQEuD+DWmwDQEIQKB8Akvz9tLryyeEhxCAAAQg4AiQ74mDLQkg0G9Jm7IgAAEIJAjQ8SegsAsCByHA/XuQhsJNCEAAAg2BpXl76fU0BAQgAAEIHIMA+f4Y7XQWLxHoz9KS1AMCEDgsATr+wzYdjkOAlTXEAAQgAIGDEVg67lp6/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+Odlxei9ejcsnn/ny3tlL72qNsQQACKxGg418JJGYgsAMB7t8doF+tyNR4LLXvalyoLwS+JLA0by+9/ku3uQwC8wmk+orUvvmWuQIClyBAvr9EMxdTSQT6NZri/aoe97sXuP0NfL9Xj1cgdK9RRm4bqY46tS+3Hyez/37WcdF58HGyOlKd5QTo+JczxAIE9iLA/bsX+YnlMkabCOp6pzFGu16bq8ZL8/bS6+UHn4UToP8ouoHI4UU3z2mcI9+fpikPUREE+qXN9HpU99utXn3+eFSPR/A9XI2+tJzc16fE+NS+3H58Zf9VPVwb3J9VaY9FGDh81aCXu4iO/3JNToVPRID7t+DGZIxWQOMwRiugEXAhIrA0by+9PnKHryUSoP8osVU6PjHP7uDgSyYC5PtMYDGbJIBAn8Qyfefr4cT5exVr8a7DONSq6ZQYn9o3Hc2GZ5Y7+dsQAkUdmAAd/4EbD9cvT4D7t9wQYIxWQtswRiuhFfChS2Bp3l56fdcbvpVIgP6jxFbBJwhsT4B8vz3zK5eIQL+o9d/V8+4E+kf1WmSngItTYnxqXwGu9l1g8tdnwp4jEaDjP1Jr4SsEugS4fw+uuOcAABK7SURBVLs8yvnGGK2MtmCMVkY74EVIYGneXnp96AvbJRKg/yixVfAJAnsQIN/vQf26ZSLQL2p7dd636jFJoX9Xr8fdXonjbvb7/VH1XlffCOPO5jv48zq3Ut/ebf9+Vg//cKBewf+Il/BbveaV2Vn1PyjQT7RpPsQbE65vyu69tub9rPk1r7OpVzfUrxhS8vSfnQaZUJ5zcYx7ku+7ej3bVxrV7fnsPqwZYxhdexv67YLZfsW8+V46AcVu6X7iHwQg0CfA/dtnUsYexmiKzeRYc7CRJoyZGKO19BijtSwOtKV741uXl17/bblctxUB+g/F+OT+YywXSuyYpF+8a/3DdI4RraMps6NfVBPm5z6M+ucxF9/q/jpWOboXjuU13h6VAAL90pbTJMWJ7Y/XyDvQ1dHfq/vjWb1er0DcjV6RI5vND8/e/bvt2x+hvT+a7fund97PL7PTwQ10evVfDUyoR5LtdJ8kvodae+/PDd+v6vWSaP+ono6r+2cvo59engR61zm7ROwGJI/ggUqHjdfz6wcDnfa8p9uye618cu/Nv/vfLeiUE1bYMYzj4YNfSezsLJoAHX/RzYNzEBglwP07imffg+o/GaMlX8fYbxyNTz6P8RijNfQUYxPHjn3m7NmDwNK8vfT6PepMmTMJ6N6m/5jWf4iXcuGX+oW9V/6ueX27KLE7n27nyOF+9U2j8/NKfR1z8Zl3xSVPJ99fstl3qzQC/Qrou6vcnVD/DATiugB1NrH2WmlFeHhAHVz0bnvZcEki7IjMRvQjqTo/NO29GSmzY7fxI9w3y2aC7bzrmz+L1iuEEv7URQz/+fSs8ga4p/k2HXvEvFflhM/y6dZrGNU3LfL3futA7fjJh55T7CiNAB1/aS2CPxCYToD79/+3d2/XjcJAAEBTVwpKPa4mzaQY7wF7bCwesSIWD/h+7CEEhIYrGAnZYZ+3esWexmjn820cMxp3PLZIjE9Gu8V442FDjFmur3mcGO9cjm6MdvvOyCO3tRcKtObt1vIvPHVVVwjoP57vP25fKGucvzj/fJ9/Rklzph8Z9TvPPZ9HX+dZvOJmeONd5fs3bvwXnLoJ+tXQyz+T6l5HEwePzqJ7nc3P+efh3/flVTXDSdZRZ3M9zuQDUrctPgUevgt/hTpHcVQeM07/tvxD+WsMH92n8B/dp9ynib9SmOm0w6V/jVCDexwnPijozyfMP8+n+9f1b2d6+2HO8OFYt73PMWAYfigSA56H3z3EMGz3+7H8tB8BHf9+2kqkBEoB928pknHdGK1/LeLkGCrayxhtejwdPt3nHNe/sBy+9nA0zov9Y5xojBYimZatebu1fCYLsfwmoP/4vf+Y/jZ7L1s1fzHXFjP5dJR/Y7+l5/PYZzo3y/NzbfC+v5fv37ftX3HmJuhXV+868XgdTST++JbRxLvSu0nncuJ51NlEkNfj3Gf+rxumOpoV6hzFUXnMCPu2/Fv5+FO10TfIy+OOHjwr6xudb1Qw5Xv5RsHt/wHoXlVzmnjF0eiY15hGsV7ruu7/8In+6Bi/xBWbLXcjoOPfTVMJlMBIwP07Ikn8C2O00RcTb61VOWa6ljNG+7q8FnE4ad/bzIwdb95+eKVAa95uLf/Kc1f3XwX0H/P9x8IE/fnatzw1fxFt072H/nQ+9a/JGb7SN+ZWrvtNPSMP33M/+XzuWTyULZ8TkO+fc7LXOgIm6NdxHB0lHlgufdG9Ixh/g/76ze7hEaY6m357TQe3Qp2jOCqPOTynYfyf3SuAym+0Tzj0ZeIB5/JBxqhvL477OHCojHd0vnECEUMxKLhu7gYQt4n64s/6xt9+v8f0GOv1YNcYTNCH/Xssdfzv0c7O8pgC7t/9tasx2lSb3ccnxmhTf615n4AyRpu6fvb1u9a83Vp+X1qiHQroP4Yag59nn6OvfcvoIX7m+fr76/wZX2AcLYtn8dk6z/0E//Tz+b2v8yw+aD8/zgrI97M0NvwHARP0/wG1O+Rj5z3TAc3VPdvZ1HRwK9Q5iqPymKPzqy8ff2bWfTu9f8XN5Kth5jrayvpG5xsn8NxxuvcU9gl8OAAZHXP5WHG+D6+zGR2jLq7Y2zKvgI4/b9uIjMBvAu7f34TybTdGm2qT5fHJZInrX4waoxX/N1SPVe85Zex3/0egNW+3lv8/Z+WoWwjoP2aUZ59X/zJ/0b0qeDh9PpNPZ+u8xzh+Pp851rWIZ/G7nZ8uAvK9K2FLARP0LdrdO9X695sXB/kZTyZPJvso1n+bPFbu39B5mKTtN9d0cDPvyoxqnqlzotOrOo+oa7CsKh/vrIvXwVzjefjmUn/s+Y62qr6J872EPn/8wal1DXf5EGFxgv7+4c2ofW/XzfR/Ejvaf/Ld+I8RWduHgI5/H+0kSgJTAu7fKZUEvzNGe2yEctz3uLVfqxozGaNdBJvHjhMN4Vf/XaA1b7eW/+8nqII2Af3Ho98T/cf4r8bjEBPPx/2mqefr677x7B+H6J6xP7u/pn/+G/S3ohPP5/Ehy+jZ2rP4nc1PNwH5/kbhhw0ETNC3IMfDSf8O+cv70b6+4v3z5bdprh3Ox8f58+t0Pn1/n7/7d6vV/IdTNR1cd2KNdU4+dFQcc9L22fLRaT9OVkeHOpwD78/0K97l37XD5/nztsOz9S19MBKxDAYFfdt39ZzO39e2jD+ju1V9CWzi3aT3mD66d+P179ebu24q45o098vsAjr+7C0kPgLzAu7feZuXbjFGWx5rTjbOfXyyPFaNcZEx2vykVBgNxo6T5n75CoHWvN1a/hXnrM4KAf1Hff8xOW/QmV/7lYcH5O730zkynvXjGft0Gr7ypsinZZ3PPp9HTP0cjmfxijvjLXeV79+y2V920iboW+l/vs+nbkJ48I60y7fqh3+WFZX8nL+LfT8+v86nhz/hWpqQrevgLrU21Fl2enEa5yePedu//OH38rPf4roNmIoOuuto+0/WLxP1j5+I/15fH+HC+Z5Gn9qvcMziWuium9G10AVWFVdpbX0PAjr+PbSSGAlMC7h/p11S/NYY7fLqvbnxxWQj/T6+MUYbwBmjDTD282Nr3m4tvx+pN45U/1HXf8zmwtr5i59+biXusY+Py+tuLhP3xfP/qM7f+6/7FX2pp5zD8Sx+F/LTRSCuRR4EthAwQb+FsjoIECCwIKDjX8CxiUByAfdv8gYSHgECBAqB1rzdWr4IxyoBAgQIJBWQ75M2zEHDMkF/0IZ1WgQI7EdAx7+fthIpgVLA/VuKWCdAgEBugda83Vo+t47oCBAgQCAE5PuQsNxCwAT9FsrqIECAwIKAjn8BxyYCyQXcv8kbSHgECBAoBFrzdmv5IhyrBAgQIJBUQL5P2jAHDcsE/UEb1mkRILAfAR3/ftpKpARKAfdvKWKdAAECuQVa83Zr+dw6oiNAgACBEJDvQ8JyCwET9Fsoq4MAAQILAjr+BRybCCQXcP8mbyDhESBAoBBozdut5YtwrBIgQIBAUgH5PmnDHDQsE/QHbVinRYDAfgR0/PtpK5ESKAXcv6WIdQIECOQWaM3breVz64iOAAECBEJAvg8Jyy0ETNBvoawOAgQILAjo+BdwbCKQXMD9m7yBhEeAAIFCoDVvt5YvwrFKgAABAkkF5PukDXPQsEzQH7RhnRYBAvsR0PHvp61ESqAUcP+WItYJECCQW6A1b7eWz60jOgIECBAIAfk+JCy3EDBBv4WyOggQILAgoONfwLGJQHIB92/yBhIeAQIECoHWvN1avgjHKgECBAgkFZDvkzbMQcMyQX/QhnVaBAjsR0DHv5+2EimBUsD9W4pYJ0CAQG6B1rzdWj63jugIECBAIATk+5Cw3ELABP0WyuogQIDAgoCOfwHHJgLJBdy/yRtIeAQIECgEWvN2a/kiHKsECBAgkFRAvk/aMAcNywT9QRvWaREgsB8BHf9+2kqkBEoB928pYp0AAQK5BVrzdmv53DqiI0CAAIEQkO9DwnILARP0WyirgwABAgsCOv4FHJsIJBdw/yZvIOERIECgEGjN263li3CsEiBAgEBSAfk+acMcNCwT9AdtWKdFgMB+BHT8+2krkRIoBdy/pYh1AgQI5BZozdut5XPriI4AAQIEQkC+DwnLLQRM0G+hrA4CBAgsCOj4F3BsIpBcwP2bvIGER4AAgUKgNW+3li/CsUqAAAECSQXk+6QNc9CwTNAftGGdFgEC+xHQ8e+nrURKoBRw/5Yi1gkQIJBboDVvt5bPrSM6AgQIEAgB+T4kLLcQMEG/hbI6CBAgsCCg41/AsYlAcgH3b/IGEh4BAgQKgda83Vq+CMcqAQIECCQVkO+TNsxBwzJBf9CGdVoECOxHQMe/n7YSKYFSwP1bilgnQIBAboHWvN1aPreO6AgQIEAgBOT7kLDcQsAE/RbK6iBAgMCCgI5/AccmAskF3L/JG0h4BAgQKARa83Zr+SIcqwQIECCQVEC+T9owBw3LBP1BG9ZpESCwHwEd/37aSqQESgH3bylinQABArkFWvN2a/ncOqIjQIAAgRCQ70PCcgsBE/RbKKuDAAECCwI6/gUcmwgkF3D/Jm8g4REgQKAQaM3breWLcKwSIECAQFIB+T5pwxw0LBP0B21Yp0WAwH4EdPz7aSuREigF3L+liHUCBAjkFmjN263lc+uIjgABAgRCQL4PCcstBEzQb6GsDgIECCwI6PgXcGwikFzA/Zu8gYRHgACBQqA1b7eWL8KxSoAAAQJJBeT7pA1z0LBM0B+0YZ0WAQL7EdDx76etREqgFHD/liLWCRAgkFugNW+3ls+tIzoCBAgQCAH5PiQstxAwQb+FsjoIECCwIKDjX8CxiUByAfdv8gYSHgECBAqB1rzdWr4IxyoBAgQIJBWQ75M2zEHDMkF/0IZ1WgQI7EdAx7+fthIpgVLA/VuKWCdAgEBugda83Vo+t47oCBAgQCAE5PuQsNxCwAT9FsrqIECAwIKAjn8BxyYCyQXcv8kbSHgECBAoBFrzdmv5IhyrBAgQIJBUQL5P2jAHDcsE/UEb1mkRILAfAR3/ftpKpARKAfdvKWKdAAECuQVa83Zr+dw6oiNAgACBEJDvQ8JyCwET9Fsoq4MAAQILAjr+BRybCCQXcP8mbyDhESBAoBBozdut5YtwrBIgQIBAUgH5PmnDHDQsE/QHbVinRYDAfgR0/PtpK5ESKAXcv6WIdQIECOQWaM3breVz64iOAAECBEJAvg8Jyy0ETNBvoawOAgQILAjo+BdwbCKQXMD9m7yBhEeAAIFCoDVvt5YvwrFKgAABAkkF5PukDXPQsEzQH7RhnRYBAvsR0PHvp61ESqAUcP+WItYJECCQW6A1b7eWz60jOgIECBAIAfk+JCy3EDBBv4WyOggQILAgoONfwLGJQHIB92/yBhIeAQIECoHWvN1avgjHKgECBAgkFZDvkzbMQcMyQX/QhnVaBAjsR0DHv5+2EimBUsD9W4pYJ0CAQG6B1rzdWj63jugIECBAIATk+5Cw3ELABP0WyuogQIDAgoCOfwHHJgLJBdy/yRtIeAQIECgEWvN2a/kiHKsECBAgkFRAvk/aMAcN6yMuOMuPMwMGrgHXwCuvgYP2M06LwKEFXpkz1K3Pcg24BlwDf78G/to5Mf+7OTt2rgHXwB6vgb/2F8oRqBEwQf8hQe4xQYrZdXvEa6AmeduXAIEcAkfMRc5JH+sacA28wzXw117kHWycoxzgGnANuAbu18Bf+wvlCNQIeMVNjZZ9CRAgQIAAAQIECBAgQIAAAQIECBAgQIDASgIm6FeCdBgCBAgQIECAAAECBAgQIECAAAECBAgQIFAjYIK+Rsu+BAgQIECAAAECBAgQIECAAAECBAgQIEBgJQET9CtBOgwBAgQIECBAgAABAgQIECBAgAABAgQIEKgRMEFfo2VfAgQIECBAgAABAgQIECBAgAABAgQIECCwkoAJ+pUgHYYAAQIECBAgQIAAAQIECBAgQIAAAQIECNQImKCv0bIvAQIECBAgQIAAAQIECBAgQIAAAQIECBBYScAE/UqQDkOAAAECBAgQIECAAAECBAgQIECAAAECBGoETNDXaNmXAAECBAgQIECAAAECBAgQIECAAAECBAisJGCCfiVIhyFAgAABAgQIECBAgAABAgQIECBAgAABAjUCJuhrtOxLgAABAgQIECBAgAABAgQIECBAgAABAgRWEjBBvxKkwxAgQIAAAQIECBAgQIAAAQIECBAgQIAAgRoBE/Q1WvYlQIAAAQIECBAgQIAAAQIECBAgQIAAAQIrCZigXwnSYQgQIECAAAECBAgQIECAAAECBAgQIECAQI2ACfoaLfsSIECAAAECBAgQIECAAAECBAgQIECAAIGVBEzQrwTpMAQIECBAgAABAgQIECBAgAABAgQIECBAoEbgH6WiRri5sayzAAAAAElFTkSuQmCC[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABegAAAF1CAYAAACTcQoTAAAgAElEQVR4AeydPdKruNa2PZgTdNWegZMOO9kjOPEpRx2dCXS8M4edfVEP4CSO33l4MHwlwb0QQmAwCARcXbXbmJ+lpUuLJelGD75V/AcBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMDmBG6bl0iBEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIVAj0BAEEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0GeCfrvdKv7BgBggBogBYoAYIAaIAWKAGCAGiAFigBg4VgysJRPQ7sdqd9qL9iIGiIHdYmCtjgc7XQK7NSgPBngwQgwQA8QAMUAMEAPEADFADBADxAAxQAx8HQPd2f3339AFEPuIAWKAGCAGJsXA910NV44REPzq/27V0n9ma6xAjkEAAhCAAAQgAAEIQAACEIAABCDwNYG1595r2/u6YlwIAQhAAAJFE+AVN5maxzriSKB3+8cE+9Rxs5XJV8xCAAIQgAAEIAABCEAAAhCAAASuTmDtuffa9q7ePtQfAhCAwFkJINBnalnriCOBfkycHzpmtjL5ilkIQAACEIAABCAAAQhAAAIQgMDVCaw9917b3tXbh/pDAAIQOCsBBPpMLauO2H0OCe9u/5TjspXJVcxCAAIQgAAEIAABCEAAAhCAAAQuT2Dtuffa9i7fQACAAAQgcFICCPSZGtY6YlbQZyKMWQhAAAIQgAAEIAABCEAAAhCAwHoEbB6/ksm17a3kFmYgAAEIQKAwAgj0mRrEOuJIoHf7566oN1uZfMUsBCAAAQhAAAIQgAAEIAABCEDg6gTWnnuvbe/q7UP9IQABCJyVAAJ9ppa1jjgS6MfE+aFjZiuTr5iFAAQgAAEIQAACEIAABCAAAQhcncDac++17V29fag/BCAAgbMSQKDP1LLqiN3nkPDu9k85LluZXMUsBCAAAQhAAAIQgAAEIAABCEDg8gTWnnuvbe/yDQQACEAAAiclgECfqWGtI2YFfSbCmIUABCAAAQhAAAIQgAAEIAABCKxHwObxK5lc295KbmEGAhCAAAQKI4BAn6lBrCOOBHq3f+6KerOVyVfMQgACEIAABCAAAQhAAAIQgAAErk5g7bn32vau3j7UHwIQgMBZCSDQZ2pZ64gjgX5MnB86ZrYy+YpZCEAAAhCAAAQgAAEIQAACEIDA1QmsPfde297V24f6QwACEDgrAQT6TC2rjth9Dgnvbv+U47KVyVXMQgACEIAABCAAAQhAAAIQgAAELk9g7bn32vYu30AAgAAEIHBSAgj0mRrWOmJW0GcijFkIQAACEIAABCAAAQhAAAIQgMB6BGwev5LJte2t5BZmIAABCECgMAII9JkaxDriSKB3++euqDdbmXzFLAQgAAEIQAACEIAABCAAAQhA4OoE1p57r23v6u1D/SEAAQiclQACfaaWtY44EujHxPmhY2Yrk6+YhQAEIAABCEAAAhCAAAQgAAEIXJ3A2nPvte1dvX2oPwQgAIGzEkCgz9Sy6ojd55Dw7vZPOS5bmVzFLAQgAAEIQAACEIAABCAAAQhA4PIE1p57r23v8g0EAAhAAAInJYBAn6lhrSNmBX0mwpiFAAQgAAEIQAACEIAABCAAAQisR8Dm8SuZXNveSm5hBgIQgAAECiOAQJ+pQawjjgR6t3/uinqzlclXzEIAAhCAAAQgAAEIQAACEIAABK5OYO2599r2rt4+1B8CEIDAWQkg0GdqWeuII4F+TJwfOma2MvmKWQhAAAIQgAAEIAABCEAAAhCAwNUJrD33Xtve1duH+kMAAhA4KwEE+kwtq47YfQ4J727/lOOylclVzEIAAhCAAAQgAAEIQAACEIAABC5PYO2599r2Lt9AAIAABCBwUgII9Jka1jpiVtBnIoxZCEAAAhCAAAS2IPB6uAUF9+r53qK0fGWcpR75CGEZAhCAAARsHr8SirXtreQWZiAAAQhAoDACCPSZGsQ64kigd/vnrqg3W5l8xSwEIAABCFyYwOvh/5rrHqqvqX0XRnTOqr+r590J74/qNVbB97O6327V7TF61piFMo6dpR5l0MQLCEAAAqclsPbce217pwVPxSAwRCA1L0ntG7qe/RA4CAEE+kwNZR1xJNB3xPl/bvWk9+dn0d7Z4z8IQAACELgYAYmKTiAN/93v1f3xrF5rrGhODXBT+y6Gfml13897/8HHUqOrXj9NoK9XnX8Q8Vf1K4+xs9QjDx2sQgACEICACGi8pe9LP9e2t9QfrofAqgSYqyzCWf58YVH1uHgmAVTfmcCmnq6O2H12RPlQsP+nEVxGBPqOnamFcx4EIAABCJyDgAa993v1eDzsn1/R3Aj2nZXv39Q6Jcan9n1jO/s1r+rhONyf1RrPKtZ0t/wB9wSBvom/chfPT2z/4uuxZuRhCwIQgAAElhDQ/HuJjfDate2FttmGwO4EmKssaoLy5wuLqsfFMwkg0M8ENvV064hDQT7eZgX9VJycBwEIQOCaBDToTSik71fz6pHbrUocns4rJcan9k23uOGZEwXaDT06TlETBPriK0P7F99EOAgBCEDgYARsHr+S32vbW8ktzEBgHQLMVdbhiBUIVFWFQJ8pDKwjjkR5t99W1CcE+s7x5lqzlclXzEIAAhCAQKEERga93uNGSP/4HvGx6qXE+NS+MRu7HUOg/R49Av337LgSAhCAAATOSmDtuffa9s7KnXodlABzlYM2HG6XSACBPlOrWEccCfQmzrv9CYG+cxyBPlPrYBYCEIDAQQh8GvRWElnjVfTv6v16VHf/I6B6f/29eoQ/BCsEKTE+tc+f/65ej3v9+yl6xc79MeNd+BOub8ruvbZGLJrX2dTvFFfdgs/OnxNMKM/VqynTXeq52fv+B5hV7+r1fEQcnt0fWx1jGF17c68wSv2gwGy/1KjR5/tVPR/1O/H9+MS3mWIn9X75OdzulQurON7uj9fAa4f67KbU38VdPba6V8+Xa7Kgza294h+znViPVWI7Ys5XCEAAAhA4JAGbx6/k/dr2VnILMxBYh4DG553xd2ha480DzFXGxt0ap7+f1cPmV8PzhHhcfLsNnJucL/THyvd7NM/wiPvnTRlTT5vrhG3I9lYEEOgzkVZH7D5TorvfxzvoM9HHLAQgAIGTEPg46K2q1LsLbd/9UT1fr+r1ageTvXfWpwaGqX32MKD5gVpn14TmWqQdp64B+ufrJb6GY/16X1DOu66Xfx+/1fMVPCyYXp4Eejeodf32/e7e998+iIiZyT//Q73icA98cyBGGbr35ut3BYJywgoHNqb6lebf/JWBf1d//TsG3Qc3sUA/l9u9une4BQ8u4vpYDM2svxfgXdw8qofj/KrcEwEf16u0v/n1OTbTjNkLAQhAAAJnIaB5/Fr1WdveWn5hBwKrEDjTXKUZu9u42//+lxaI3Kq7Fov4eUI73o3nCUvnYZPmGTZ2nTmm7ozZgzlIahHXKgGCkTkEEOjn0JpxrnXErKCfQY1TIQABCECgQ2DCoDcpBL9f1bv3q6kDr4NJCcmJfRps9jXX5l34vQOdmtiDhN5pyTpKVG7E44Q/tfWBOjn99lkPqCeVpwH5LRLZ5VvnR2gbAbuzr1tX/y3hs3y69ZxSfaPyZ/mV8CHgMDR5iF+PJB97LopFeGDIvypdH9leXH+r6jrtL7/CqvkiUnW2stmAAAQgAIEzErB5/EqVW9veSm5hBgLrEJgyVkqMid1Ci9LmKppTudXuoV6tcaK7lzvjadU9nhMsqtu0eYb51Bu8psfgQ3WrhuqwTnRgZSYBBPqZwKaebh1xJNC7/baiPvGKm85xXnEzFTfnQQACEDgnAQ2aeoOvtroaoHUGjO3hYEsro6MV06lBc2+fBovudTbv6t3596r/1DMenAYlV1rl0bxaZdL1En/d6hW/+vuZeGXKkEA7099efeV8ipn2uZXcvacgujCxgl7XRfybK5LtOMuvtuh2a6zM1LFm39R2GvSvfUDSxmWqvMDT5oFKe/7QXyG011R6ENCLvTn1mHNuWDbbEIAABCBwRgI2j1+pcmvbW8ktzEBgHQKnmauMjDsH6zg+tu0CHji3N5bWeWPzDJ2z5ZyiWxu+5SGAQJ+Ha/Oe1ECMj4R6veLG/2n2z/Hz6NQzNRJmIQABCJROYHBA2DouYbev4bv30D+rp//zzObVJv5VIdFgrjcwTA1QtRpj4L3fgwK6/Pzuev2JZ7ySRVaHBdqZ5aUY+EIGBsDh+yfdq2qeifet92wOPUxoatOc31ld3rOhmg/4pcP2OVZmysZa3EZiqCemf1N/VXCofnPqMedclcsnBCAAAQiclcDac++17Z2VO/U6KIHTzFVSY1e1STNW7E22UmNpXbNgHvZxnjE0/m3KzjKnUL34zEkAgT4TXXXE7tNWzMciPe+gz0QfsxCAAAROQuDjoFcDw+6fYro/Y/QPgL0gH4vqCwR69wNFndXzwWr6UeTtQHL69apb7X9vTOzLa+1217K3+yeV96UQ7h6AhD8UFf45rP6UtF0R3vrU9bUBl2UwPVam+Ibx0J6/jFtqktPaXl5/BduQzXb/53rMOVfl8gkBCEAAAmcloHn8WvVb295afmEHAqsQOM1cJTV2FaFmrNibjKTG0rWdRfOwptjheUY7dl0+ph6og6rO56YEEOgz4baOOBblw++JV9ykxHyzlclXzEIAAhCAQKEEPg16dbyzKlkDrXv16LyCRftDQXZgMNoTrAeunYxt/vX2lwHPZhB6i/z2ZQ8NUGeW16uvKjbNznuSuD5uS/VtBf2BtvGujduS9/ZqoSS7lI3UvtZab2uQW/uKm3YuM257Xv3lyRrtP+6XSuITAhCAAASuQWDtuffa9q7RCtTyMAQ0F2kHfF3Xdbz4ucrYuLsZb/bqmBpDat+CeViXYNWfZ6iM1NyoHYOvO6eInOJrFgII9FmwVoOvuHEdtInwCYG+c7wR8+nUMzUSZiEAAQiUTkCD2t6A0P/6p62S7x4eEi2bd8XHYm1KZE3sSwqo4udX1etL+nPW9aq3BvMpAdwXMzxAnVVeor51LYbtd2uZGLgnbOqVPZ0BszP0bq6PfpSqvwpfpU71y70Kv/4LhG6Z7+r1qH9Ed+hHYrvnN+XG7ax2if3Wu+Gj/Wlfvqn/Zw5z2n/OuSqZTwhAAAIQOCeBtefea9s7J3VqdVgCGrN3JyN1dXTsdqu6h8ucqwyPuxPjfF/D1Hh8hbr1gqFf/npj6lQdeg6wYyMCCPSZQFtHHK6Yj7cTAr2J98G5ZiuTr5iFAAQgAIFCCWhg695z3nuXvBNe3fvP+3/caIO2x7N6vV7V8xm+8iZabZEQktMD1GZweLtV98ezer5e1cu/474WepOCbgfr1Os1UOy+tkd16g7wWwH6dnfv2b9XdzthanljK2bkS8DMt4krp2brGOg1N1a0q3eKqwnXt+pmbSqh/Fb1GCZtOOMJvzqsgy+KIddunpFi4V7d7y6Ggrr5y+Zz0ziltn+3B0e9+qxW/7Z+iotF7R/49V1st/6wBQEIQAACxyagPm2tWqxtby2/sAOBVQhonGnj2vB3rw42Vxkcdzdj485A39FLj8c1NtVcYdY8bOo8Ixi7bjanWCVgMDJGAIF+jM6CY+qI3WdKdPf7eAf9AsJcCgEIQOACBDTojd8lrx8m7WvzDZR39bQV0s3g+OVWTScE2dRgNLXPW65XXnfeq3h/VM/Oq3TG2uXz9YOrmY1FQlD2QrOrWyxyfy7PeztS32dPxF7BpnuQELSpE7aTDGf5NcLdrdAPGbmHC2893Ih5Ojvz6/juPASK/6w39K2OzWX1D+1Fdes8sJpYD29uzrlh+WxDAAIQgMCZCGgev1ad1ra3ll/YgcAqBGx8Xo/DFe9eNH6+qveR5iqD4+55Ar0X7r+eh80Zj64xpk4/ZFglNjAymwAC/Wxk0y5QYhoU54MV8p/OMVvTiuYsCEAAAhCAAAQgkJ/A4EQmf9GUAAEIQAACEMhBYO2599r2ctQZmxCAAAQgsD8BBPpMbWAdcSTEu/1jgnzquNnK5CtmIQABCEAAAhCAwGwCCPSzkXEBBCAAAQiUTWDtuffa9sqmh3cQgAAEIPAtAQT6b8l9uM464kigHxPnh46ZrQ9lchgCEIAABCAAAQhsRgCBfjPUFAQBCEAAAtsQWHvuvba9bShQCgQgAAEIbE0AgT4TcXXE7nNIeHf7pxyXrUyuYhYCEIAABCAAAQjMJ4BAP58ZV0AAAhCAQNEE1p57r22vaHg4BwEIQAACXxNAoP8a3fiF1hGzgn4cFEchAAEIQAACEIAABCAAAQhAAAIFELB5/Eq+rG1vJbcwAwEIQAAChRFAoM/UINYRRwK92z93Rb3ZyuQrZiEAAQhAAAIQgAAEIAABCEAAAlcnsPbce217V28f6g8BCEDgrAQQ6DO1rHXEkUA/Js4PHTNbmXzFLAQgAAEIQAACEIAABCAAAQhA4OoE1p57r23v6u1D/SEAAQiclQACfaaWVUfsPoeEd7d/ynHZyuQqZiEAAQhAAAIQgAAEIAABCEAAApcnsPbce217l28gAEAAAhA4KQEE+kwNax0xK+gzEcYsBCAAAQhAAAIQgAAEIAABCEBgPQI2j1/J5Nr2VnILMxCAAAQgUBgBBPpMDWIdcSTQu/1zV9SbrUy+YhYCEIAABCAAAQhAAAIQgAAEIHB1AmvPvde2d/X2of4QgAAEzkoAgT5Ty1pHHAn0Y+L80DGzlclXzEIAAhCAAAQgAAEIQAACEIAABK5OYO2599r2rt4+1B8CEIDAWQkg0GdqWXXE7nNIeHf7pxyXrUyuYhYCEIAABCAAAQhAAAIQgAAEIHB5AmvPvde2d/kGAgAEIACBkxJAoM/UsNYRs4I+E2HMQgACEIAABCAAAQhAAAIQgAAE1iNg8/iVTK5tbyW3MAMBCEAAAoURQKDP1CDWEUcCvds/d0W92crkK2YhAAEIQAACEIAABCAAAQhAAAJXJ7D23Htte1dvH+oPAQhA4KwEEOgztax1xJFAPybODx0zW5l8xSwEIAABCEAAAhCAAAQgAAEIQODqBNaee69t7+rtQ/0hAAEInJUAAn2mllVH7D6HhHe3f8px2crkKmYhAAEIQAACEIAABCAAAQhAAAKXJ7D23Htte5dvIABAAAIQOCkBBPpMDWsdMSvoMxHGLAQgAAEIQAACEIAABCAAAQhAYD0CNo9fyeTa9lZyCzMQgAAEIFAYAQT6TA1iHXEk0Lv9c1fUm61MvmIWAhCAAAQgAAEIQAACEIAABCBwdQJrz73Xtnf19qH+EIAABM5KAIE+U8taRxwJ9GPi/NAxs5XJV8xCAAIQgAAEIAABCEAAAhCAAASuTmDtuffa9q7ePtQfAhCAwFkJINBnall1xO5zSHh//Vm/g17n3n/cqlck6OuYt5PJV8xCAAIQgAAEIAABCEAAAhCAAASuTkDz77U4rG1vLb+wAwEIQAACZRFAoM/UHtYRR4K7xPrXz1qcv/+8Va9ft8qJ9U6gf/7TF/TNViZfMQsBCEAAAhCAAAQgAAEIQAACELg6gbXn3mvbu3r7UH8IQAACZyWAQJ+pZa0jjgR6t9+J9M8ft+r241a9B45LyHefssUnLIgBYoAYIAaIAWKAGCAGiAFigBggBogBYoAYIAaIAWKAGDhRDGTSpy9vVjdJKLSH216gv92q56/+ivnwPAT6E91sN+qi+4JPYoEYIAaIAWKAGCAGiAFigBggBogBYoAYIAaIAWKAGLhVrKDP9CghDK5YcPff/7lVD7eK3om2P27V48/+avpYnM/kKmYPQKATT//7f1XV/HP7te0++Q4P4oH7QzFAPiAfKBboH+gfyQf1mPsAQz5c3ICAux/CeyLcJl+SL3PEg7e5QWxTxPYEXNvSvttzp0QInJEAAn2mVrVEHb3CJhbr378Cod6tqOcd9Jla5NhmLZ4Q5v0DCT8I4kGFPZyBB0IsQiwPZhQD5APygWIBobEVGm0cdezhIN6vREDxQL4kX26RLxVvK4UvZgojQPsW1iC4A4EDE0Cgz9R4lqgjgd4PBKN9TrR3Qv3YNf66TL5itnwCig0fBwjTCNM8qOFBDX8x01n9iBDZCpESG+gvEJ4UC9wf9f3BWLr88e5WHmpcrXuEfEm+VCzkypfkn63u7u3LsXyyfdGUCAEInIwAAn2mBrVEnRDj41X0+v5wfx71s/9OerOVyVfMlk/AYgBhFmEWYRZhlldb2UO6XBPp3BN17PMXD4oB179r233yPQ8PG0eVP+TDww0IKB643/Lcb8pp8K35Kt42CG2K2IEA7bsDdIqEwEkJINBnalglaj8wiUX6f27V/Xar7j/rVfOv4DU3j+hHYzt2MvmK2fIJdOKAFfQmZvj7Cx7w4MGVjwHuB4QGiSIIvQjd5IN+PvBMyh/y4eEGBFwshPdIuE3+JH/miAdvc4PYpojtCbi2pX23506JEDgjAQT6TK1qiToW55vvr5+1SK/z3A/FPiNxXivrdU4mVzF7AAIWAwiRCJGssOxMqplIM5F2+RFhmhXpigHigftBsRD2DzaOOsCYDxfzE1A8kC/IF6l8oX1rxYfiLX9kU8IeBGjfPahTJgTOSQCBPlO7WqKOBHrf0Uf7JMS7z9Rxs5XJV8yWT0Ax4OODFeMmxsGDiZUmUaEQo33EB/GhWCA+eJBDPiAf+Bgof8iHhxsQcLEQ5oRwm/6C/iJHPHibG8Q2RWxPwLUt7bs9d0qEwBkJINBnalVL1CNifCjMj22brUy+YrZ8AhYDrKBnBT0r6DuTaibSTKT9pIgHlzy4pH+kfxzpH20cVf6QDw83IKB4oP/gwd0WD/IVbxuENkXsQID23QE6RULgpAQQ6DM1rBK1H/iNiPRTjstWJlcxewACigEfLwhRCFEIUQhRI0KUJpvkC4QHxQIPsniQRT5gheMBhrubuahxtXIk9wf9pWIhV3/pY2yzCKegLQlYPtmyUMqCAAROSQCBPlOzWqIeEefHVs2Hx8xWJl8xWz4BiwGEWYRZhFlW0PPOdXtIl2sinXuijn3ema8YcP27tt0n3/PwsHFU+UM+PNyAgOKB+y3P/aacBt+ar+Jtg9CmiB0I0L47QKdICJyUAAJ9poa1RB0J9H6gEu2Lxfjwu9s2W5l8xWz5BBQDPn5YQW9iBjyYWGkSiLCFsEc+IB+QD3jwoRhI5QO/r/whHx5uQMDFQhgj4TbjCcYTOeLB29wgtiliewKubWnf7blTIgTOSACBPlOrWqIeEeNjIX7ou9nK5CtmyydgMcAKelbQs8KyM6lmIs1E2k+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7s6qFezvGk4m2D0KaIHQjQvjtAp0gInJQAAn2mhlWi9gO/EZF+ynHZyuQqZg9AQDHg4wUhCiEKIQohakSI0mSTfIHwoFjIKTyoDOKNeFMslBpvPkYPMObDxfwEXCyEOSvcLjV+S7+/8G/8L5jIP/nv671KsHyylwOUCwEInIYAAn2mprREPSLOD62Yj/ebrUy+YrZ8ArDMTZMAACAASURBVBYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaOKn/Ih4cbEFA8XPV+uHo+2Lr+ircNQpsidiBA++4AnSIhcFICCPSZGtYSdSTQ+4FgtC8U5FPHzVYmXzFbPgHFgI8PVtCbGAcPhElNstwn8UA8EA8I0YoB8gH5QLGg/sHHRPlDPjzcgICLhTBHhNuKlzh++E7/ohj4Jl78NRvENkVsT8C1Le27PXdKhMAZCSDQZ2pVS9QjYnwozI9tm61MvmK2fAIWA6ygZwU9QnRnUs1EmgcTflLEg0seXNI/0j+O9I82jip/yIeHGxBQPNB/8CBPonvO8aTibYPQpogdCNC+O0CnSAiclAACfaaGVaL2A78RkX7KcdnK5CpmD0BAMeDjBSEKIQohCiFqRIjSZJN8gfCgWMgpPKgM4o14UyyUGm8+Rg8w5sPF/ARcLIQ5K9wuNX5Lv7/wb/wvDMg/+e/rvUqwfLKXA5QLAQichgACfaamtEQ9Is6PrZoPj5mtTL5itnwCFgMIswizCLOdSTUTaVbQu/yIMDAuDMAHPoqBq94vNo4qf8iHhxsQUDxc9X64ej7Yuv6Ktw1CmyJ2IED77gCdIiFwUgII9Jka1hJ1JND7gWC0Lxbjw+9u22xl8hWz5RNQDPj4YQW9iXHwQJjUJMt9Eg/EA/GAEK0YIB+QDxQL6h98TJQ/5MPDDQi4WAhzRLiteInjh+/0L4qBb+LFX7NBbFPE9gRc29K+23OnRAickQACfaZWtUQ9IsbHQvzQd7OVyVfMlk/AYoAV9KygR4juTKqZSPNgwk+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7kSXTPOZ5UvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfuA3ItJPOS5bmVzF7AEIKAZ8vCBEIUQhRCFEjQhRmmySLxAeFAs5hQeVQbwRb4qFUuPNx+gBxny4mJ+Ai4UwZ4XbpcZv6fcX/o3/hQH5J/99vVcJlk/2coByIQCB0xBAoM/UlJaoR8T5oRXz8X6zlclXzJZPwGIAYRZhFmG2M6lmIs0KepcfEQbGhQH4wEcxcNX7xcZR5Q/58HADAoqHq94PV88HW9df8bZBaFPEDgRo3x2gUyQETkoAgT5Tw1qijgR6PxCM9oWCfOq42crkK2bLJ6AY8PHBCnoT4+CBMKlJlvskHogH4gEhWjFAPiAfKBbUP/iYKH/Ih4cbEHCxEOaIcFvxEscP3+lfFAPfxIu/ZoPYpojtCbi2pX23506JEDgjAQT6TK1qiXpEjA+F+bFts5XJV8yWT8BigBX0rKBHiO5MqplI82DCT4p4cMmDS/pH+seR/tHGUeUP+fBwAwKKB/oPHuRJdM85nlS8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStR+4Dci0k85LluZXMXsAQgoBny8IEQhRCFEIUSNCFGabJIvEB4UCzmFB5VBvBFvioVS483H6AHGfLiYn4CLhTBnhdulxm/p9xf+jf+FAfkn/329VwmWT/ZygHIhAIHTEECgz9SUlqhHxPmxVfPhMbOVyVfMlk/AYgBhFmEWYbYzqWYizQp6lx8RBsaFAfjARzFw1fvFxlHlD/nwcAMCioer3g9Xzwdb11/xtkFoU8QOBGjfHaBTJAROSgCBPlPDWqKOBHo/EPy/W/X681bdm9Ub/twft+rxq1nNkbjGX5fJV8yWT0Dx5OOAFfQmxsEDYVKTLPdJPBAPxANCtGKAfEA+UCyof/AxUf6QDw83IOBiIcwR4bbiJY4fvtO/KAa+iRd/zQaxTRHbE3BtS/tuz50SIXBGAgj0mVrVEnUktruV8c8fdRK/OVH+Z/1PYv39560KV8+7bbOVyVfMlk/AYoAV9KygR4juTKqZSPNgwk+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7kSXTPOZ5UvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfuAXiPTvPxvBvRHiw+OP5unr859WpO/YyeQrZssn0IkDhCiEKIQohKgRIUqTTd+/kC/IF+QL8gX5gsUu5Q91N/VQ42r6y3pVPOOF/A8qPONNo5zCtiJg+WSrAikHAhA4LQEE+kxNa4k6EOfD1fOvaL87JvH+/mcr0LOCPlMDHcysxRNCC0ILQgsr6HnnuonuOVe8Idwg3BBf5/kLHRtHHWz8h7t5CCge3KdyPff7ee53tWkp7at4yxPNWN2bAO27dwtQPgTOQwCBPlNbWqKOhHi//8etekf7nRBfNe+gv0WvuTFbmXzFbPkEFAPuU4NOJhJMJIgH7gfyAe/EVQyQD8gHigXGB+nxgb9Hyh/y4eEGBFwshDkz3Ob+Sd8/5Jdl4w3yzwY39k5FWD7ZqXyKhQAEzkMAgT5TW1qijoR4/xobBPpM1M9r1uKJFfSsoGcFfWdSzUSaibSf9PIqH3t4Cw+EeoS0vpBm46jzDhWp2QwCigfyJflyi3ypeJsRopx6IAK074EaC1chUDgBBPpMDaRE7Qd+gUivH4jVK27C46lX3HTsZPIVs+UT6MQBQhRCFA9qeFDDgxoe1PAXVdYX8KCOB3V+PP1hfOTPKX/Ih4cbENC4WuLslPjRueQb8s038UL+2eDG3qkIyyc7lU+xEIDAeQgg0GdqS0vUgTjvXmPz+ln/SWX8nvnqn1uV+pFY3kGfqYEOZtbiCWEWYRZhFmEWYRZh9oMQiZDUX0EtJl4kgZ/dQ1fhYeOog43/cDcPAcXDVeKf/Ff3CXu1t+ItTzRjdW8CtO/eLUD5EDgPAQT6TG1piToS6N1+CfG3H7fq8bP+p/Pdp38ffXCdjmVyFbMHIKAY8PGBsHA5YYGJ1b4TK/jD38UA+ZdXISgXEA/HvB/8PXyAMR8u5iegcbXuafI7+V2xkCu/k3/y39d7lWD5ZC8HKBcCEDgNAQT6TE1piToQ2kPh/fnzVt2bHyhy595/3Krnr744zwr6TA10MLMWT6ygZwU9QiFCKSvo7SFdrol07ok69lnhrhhw/bu23Sff8/CwcdTBxn+4m4eA4oH7Lc/9ppwG35qv4i1PNGN1bwK0794tQPkQOA8BBPpMbalE7QcmAyK9xPdQuI+3O3Yy+YrZ8gl04oAV9CZm+PsLHvDgwZWPAe4HhAaJIgi9CN3kg34+8EzKH/Lh4QYEXCyE90i4Tf4kf+aIB29zg9imiO0JuLalfbfnTokQOCMBBPpMrWqJekScj8X4oe9mK5OvmC2fgMUAQiRCJCssO5NqJtJMpP2kiAd1PKijf6R/HOkfbRxV/pAPDzcgoHig/+g/yOJB7/p/4aV42yC0KWIHArTvDtApEgInJYBAn6lhLVFHAr0fCEb7QmE+ddxsZfIVs+UTUAz4+ECIQohCiEKIGhGiNLkmXyA8KBZ4kMWDLPIBKxzLH+1u56HG1cqR3B/0l4qFXP2lj7HtQpySNiRg+WTDMikKAhA4JwEE+kztaol6RIwPhfmxbbOVyVfMlk/AYgBhFmEWYZYV9Lyz2h7S5ZpI556oY3/9FYpi6vpLbbtPvsNDceBjofwhHx5uQEDjavID+WGL/kLxtkFoU8QOBGjfHaBTJAROSgCBPlPDKlH7gd+ISD/luGxlchWzByCgGPDxwgp6E1/gwcRqi4mVyiDeiDfFgvskHogH4uFYD1r8PXuAMR8u5ifgYiHM4eE2+Z3+LUc8eJv5Q5sSdiDg2pb23QE8RULghAQQ6DM1qiXqEXF+bNV8eMxsZfIVs+UTsBhgBT0r6BEGO5NqJtJMpP2kiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+BB6xYPWhVvG4Q2RexAgPbdATpFQuCkBBDoMzWsJepIoPcDwWhfLMaH39222crkK2bLJ6AY8PGDEIUQhRCFEDUiRGmySb5AeFAs8CCLB1nkA1Y4lj/a3c5DjauVI7k/6C8VC7n6Sx9j24U4JW1IwPLJhmVSFAQgcE4CCPSZ2tUS9YgYHwvxQ9/NViZfMVs+AYsBhFmEWYRZVtDzjm17SJdrIp17oo79Y70ahfY6fnvZOKr8IR8ebkBA8eA+ub+Pf3+rDUttT8XbBqFNETsQoH13gE6REDgpAQT6TA2rRO0HCiMi/ZTjspXJVcwegIBiwMcLK+htMgUPJpaalLlP4oF4IB4QWhQD5APygWJB/YOPiQOM+XAxPwEXC2GOCLcVL3H88J3+RTHwTbz4a/KHNiXsQMC1Le27A3iKhMAJCSDQZ2pUS9Qj4vzQivl4v9nK5CtmyydgMcAKelbQI0R3JtVMpHkw4SdFPLjkwSX9I/3jSP9o46jyh3x4uAEBxQP9Bw/yJLrnHE8q3jYIbYrYgQDtuwN0ioTASQkg0GdqWEvUkUDvB4LRvlCQTx03W5l8xWz5BBQDPj4QohCiEKIQokaEKE02yRcID4qFnMKDyiDeiDfFQqnx5mO0/CEfHm5AwMVCmLPC7VLjt/T7C//G/8KA/LPBjb1TEZZPdiqfYiEAgfMQQKDP1JaWqEfE+FCYH9s2W5l8xWz5BCwGEGYRZhFmO5NqJtKsoHf5EWFgXBiAD3wUA1e9X2wcVf6QDw83IKB4uOr9cPV8sHX9FW8bhDZF7ECA9t0BOkVC4KQEEOgzNawStR/4jYj0U47LViZXMXsAAooBHy+soDcxDh4Ik5pkuU/igXggHhCiFQPkA/KBYkH9g4+JA4z5cDE/ARcLYY4ItxUvcfzwnf5FMfBNvPhr8oc2JexAwLUt7bsDeIqEwAkJINBnalRL1CPi/Niq+fCY2crkK2bLJ2AxwAp6VtAjRHcm1UykeTDhJ0U8uOTBJf0j/eNI/2jjqPKHfHi4AQHFA/0HD/IkuuccTyreNghtitiBAO27A3SKhMBJCSDQZ2pYS9SRQO8HguG+X/UT1/uft8qJ8r3jzT6/P5OvmC2fgOLJxwFCFEIUQhRC1IgQpckm+QLhQbGQU3hQGcQb8aZYKDXefIyWP+TDww0IuFgIc1a4XWr8ln5/4d/4XxiQfza4sXcqwvLJTuVTLAQgcB4CCPSZ2tISdSjGp7YjgT5cOa9ts5XJV8yWT8BiAGEWYRZhtjOpZiLNCnqXHxEGxoUB+MBHMXDV+8XGUeUP+fBwAwKKh6veD1fPB1vXX/G2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuBX0qYb/bpPK2glyivTx33djL5itnyCXTigBX0Jsb5+wIe8ODBFQ+ueHDFgyse1Fhf4MQn+sf+gzvG0uWPd7fyUOPqrYVayqsfll4xP5F/trq7ty/H8sn2RVMiBCBwMgII9Jka1BL1iDjvRXhW0GdqgXOZtXhCiESIRHhBeEKIRIjkwaTFgBc94AGPD+MjG0eda3hIbb4koHggf/QfZOkhAg/61nvQqXj7Mly5rHACtG/hDYR7EDgQAQT6TI1liToS6P1AMNwXCfS947yDPlMLHcus4snHB0IEQsQHIUKTK+KFiadigYn2ehNtMeX+4v5SLHB/HeP+8vdsacO/16O63e7V812aY+f2x8VCmMPDbe7nY9zPR8u/Reafc9/mm9XO8slmJVIQBCBwVgII9Jla1hJ1KMantiOBXq+2CT/NViZfMVs+AYsBhFkvzjseRxuY4y/vgFYMEL/cv4oF90k8EA/EQ/7+wcZRQ0M+L5TXoq0/9/6sNtHMEeiHWiTrfsUD+Zf8u0X+VbxlDWqM70aA9t0NPQVD4HQEEOgzNakStR/4pYT5Zp/O4x30mRriJGYVJz6eWEFv4jw8mFhtMbFSGcQb8aZYcJ/EA/FAPOQX1sV4jfvN20iMC9/Pu7+fH6/2oN8X7mgPrbuFQL8uz4nWXCyEMRVuk9/p33LEg7c5MT457VgEXNvSvsdqM7yFQKkEEOgztYwl6hFxnnfQZ4J/QrMWT6ygZwU9wmBnUs1Emom0nxTx4JIHl/SP9I8j/aONo3pjxFf1cOLKVivm4/IR6GMiC7837fnh4Yrigf6DB616CJhzPKl4WxjcXF4oAdq30IbBLQgckAACfaZGs0QdCfR+IBjui15x0zvOO+gztdCxzCqefHwgRCFEIUQhRI0IUZpski8QHhQLOYUHlUG8EW+KhVLjzcdob/g3TdDtXbbWDgT6tUg2dqa1p4uFMGeF26XGb+n3F/6N/0VROv+sHP6Y24WA5ZNdSqdQCEDgTAQQ6DO1piXqUIxPbUcCffjueW2brUy+YrZ8AhYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaO6g353tXzXou1HxZdV1XVnit7t9ujCt6M463Xr8xJ/PCrF+NvVaecQKB/PWo/ZLtznvxubOgc99k/L/Yz9vHTcVdYI3Q3QnaqnLqeznZkTw69n9V95Pq6Sp/LqXyd6zp0GXUZ61VFIZuhH+ANz9G94T7dfr6TLxUDa8WD4k23MZ/nIkD7nqs9qQ0E9iSAQJ+JvhK179hTwnyzT+fxDvpMDXESs4oTH0+soLfJEzyYSGoSxcQaYYF8QD4gHyCsKQZS+cDvS40LO0JyLGbrgkZIjl6FUwvGKaG4u89bGRToa2H+/mx/llZCtLRud70XoCeU768Nz3P1C75/Ol6JR1h443voYyiI26k67+7e69+yTHGaWk4t0MeM9FCgLaNuKVbQMx4qczw0mH+UYvg8LAHXtrTvYZsPxyFQFAEE+kzNYYl6RJznHfSZ4J/QrMUTK+hZQc8KL1a4scLPHtIhRJQpREgkpX1oHy9aFLCwwMZRg2NECb7NKvZA0HaX1AJzLAb7I7132NfC9TyBPhS+axfTDwR67jdienv9J4H60/HhusbCvgR6E+e9c+IYser5Ob0cCfTdcnyj+PFAd//n+jk3FQ+lxKdyJv6c80Gz4q13/7LjFARo31M0I5WAQBEEEOgzNYMl6kig9wOvcF/0ipvecd5Bn6mFjmVW8eTjo4CJLhOJepUi7XHOiRTxTXwjLCMsk9/Pl999m34c/klgDn84dlz0jcX7+QJ9QswffSgQVGJQ+L5Vt65ybRfV/g4dH65rXa9WeE/Xs+EXPeDQK3OmPEiIy6kF+gSjRN1VzlDdBcHFQniPh9vkf/J/jnjwNhWAfJ6KgGtb2vdUTUplILAbAQT6TOgtUYdifGo7Euj13vnw02xl8hWz5ROwGGAFPSvoWUHfmVQzkWYi7SdFPLi0vyqAx/mEZT00JN99n+9sHDVxyCcRu9a4h0VrZ25Lgb4Wr5tV/sH73Vvhu65g97xWVFf1h483dQ1si1392dqqbcTC+UyBfkI5OQV68iX5cov8qntI9x+f5yJA+56rPakNBPYkgECfib4StR/4pYT5Zp/O4x30mRriJGYVJz6eEKIQonhQw4MaHtTwoIZXHVlfgHD9vXAtceoK4wtfx6njws774ssQ6OsHAZEgnlxFHlSyOR6+Dz446l5s3/yQq4T38bqG164i0A+s8g/LySnQXyn+VVfy5T75clb+6dwAfCmdgGtb2rf0VsI/CByDAAJ9pnayRD0izoer5Me2zVYmXzFbPgGLAYRZhFmEWYRZhFmEWR7UWgz4STE84PFhfGTjqIlDvlh8jlfJt2YSgnZH3G/P1Kr1jiatH1UNfiC2viK2G39v7H4S6PXjsrdI2G/dqn981o4PrYAPLrCi3Q/BxnaHrq/9b1f6D53XLyenQE/+YAX9Fg8u5uafxF2w7a7BvLStG0cp7XDtexSw+AmBCxJAoM/U6JaoI4HeDwSjfaE4nzputjL5itnyCSgGfHwgRCBEfBAiNNkgXph4KhZYMbfPijn4179nQPwRfyX0R96HeMjnhSitHm8ONuJU5z3mWmneUdcbkfkWXV81YnrwHnaJ886HjgmVdbtVrXit1+aE4neqrKac8FrvZ+hPdN2n4w5Bsq5u973zXvv4IUZNb0h4jwX66eXME+iHyu82vGuHMCbDbfIV+SpHPHib3TBMf3u/qsfdPfxqXmV1v1eP1zt9bq69CPSzyKqtZl3EyRCAAAQSBBDoE1DW2GWJekSMD4X5sW2ztYZja9nwHXc4cVjLMHZSBCwGEGa9OO94IHwhfCkGiAfuB8UCwgrCCvmAfJDKBzaOSg2yApFc54VieXtJK4jrvFsgwrfnBeKzRDanyjfCd1+gd4K6hHS9Xz41xk6dU+8L/Q0fBtR+hoJ9I7TLL//ZPV7XI1HXjuOyE/s5JJAnBHpf0Ody5gn0MfvYv7p21n6MJxlPb7DwSfHWyRGpL69H88qpW3V/PKrHI/je+yublIGV9iHQzwI5uX1nWeVkCEDgigQQ6DO1uhK1+/wkvn86LltJV+NJxdBEIXnxgp0I9Avgzb9UMeDjaYOBpCa3lIfQoVhA+ET4JB+QD8gHPBhVDBwxH3if5w/BuOKEBFwshDEcbjPeYbyTIx68zQ/3UvJ3Jvwzp3vnL2w+mFl+GIF+FkPXtlPad5ZRToYABC5JAIE+U7Nbos64gl4rZMIFLfGfn2aqnvvb28R7J7OVdnnDFk+soGcFPe+g70yqmUgzkfaTIh5c2ipIePAgRSI6+bHNjzaOuvyIEgCOgOKBfEm+3CJfKt7G7z79hUzqL1rGr1z9KAL9LKTT2neWSU6GAAQuSgCBPlPDW6KOBHo/EIz2hSvoU8fNVsfX5k9Ct1ox3ym7QqCPeSz+3rRn+LQlsKkY8PGBEIUQxYMaHtTwoIYHNbyawfoChOhWiJbYxHihLzx6JsHYis3rEtC4mvul/qsg8kU/Xyg21upfPucfCfTR71QM3qbv6vVsX4HjY3roffWN4N6fZqrM6KFAINC/3Wt37u2rt+4P90Ku+L931T3PnX+vHsnX8vT9vt+f1atjcso57oJ39Xrc7bVAjsH9/qh6r+wP6u/9tFd8Be/3fz+rR1DPtO8dJ+2LZ+/GZPwHAQhAYCEBMslCgEOXW6IeEeNDYX5s22x1ChsXdDun5vjiO7r0ex1zFHd+m+PtaTGAMIswizCLMIswizDLg1qLAdc/ri2kYO98r/KxcdT5B5TUcAIBxQP5g/y5Rb5XvH0MzUZIduenhXBZkLB+q25OlPfvq2+Fandt579AoO7st9++SAv08tuJ3uH78Ds/oN28gsf7fH9Uz9erer1asTv8fQxXdv0aH1e/Z/Vy57qHDPeupjDlHCfOP72gfu/a8uJ71179l/81q5qtq0/7Q7x3bUf1jH3vsmu/iVO7hy0IQAAC3xFAoP+O28erlKjd5yfx/dNx2eoWqk5pylP29lzZut2ijtg616hDc4WmOvVAoFcnKtvxmMD7HQw4hs+L/Yx9/HTcO1s97Kl4/bQ/9qd+NZCzHdnTic2PeA37Oa2cmltdhy6jLmO9qkjl1Z/dc8JjWwwkVYYrV9vuk+/wIB7OJ1ypTbm/ub8VC+R7+rsz5gNfJz8o5X9XJ+BiIYzxcJv8R/7LEQ/e5oQbr7vCuxGyoyXrNnfU3NXsNgu+bt15ZHIu76/RXDiac9u8PbJTDdh/v6p35GOlczt/7d+U19lnzjcbU87Rj1QndBDN40M2A/Uxju6BSLjaXzZG/Wz9dm07tX3bq9iCAAQg0CeAQN9nssoeS9TZVtB7RT34k66oY7VaNB1p1MHUgnG30607qe4+b6bp1MJ+Th29q2fYoUmIDs/1dieU768Nz3OdY/D90/FKnWlYeON76GPYGdupOu/unqa3LFOcppaTZjQwENIgxhyyBvQbFk+soPcPDPwgiBWk9vAEHgirCKs8OFEMkA/IB4oFhMZWaLRxVHd4xbeLElA8kC/Jl1vkS8Xb9NstfsWLexWLrh6aS9bHNc8N576ak7Y2PtjSvDgUrZtLkvZlrvOZ8lP77tWz9x4aXTzjHP86m3f1fof/XvWragINQfXvMHHFpbQD74Z8aDUBeZf6nN++KSvsgwAEIFBVCPSZosASdSTQ+4FgtC9cQZ86braSvqoDqZ/c3sLOyP6MLNW59IX7usOdJ9D3OjoJzZEfPdebDrG9vvGnP3JoLv10XH8y169rLOxrYNEtShyj63t+Ti9Hg4FuOQN/kSBuvZPr6isGfHwgTCNM86CGBzX8RUtn9SNCZCtESmygv0B4Uixwf9T3h78negNSdlyRgMbVukfIl+RLxUKufPld/nFCvV7Fojlqfw7fuYcbcb3zGppmX3+aOTD/HRHoNb9t5/Aq3b2H/lk9/et2wlfiyO/mvPBd7+71PM/EO+0/ntMwiP5qXve1/wy1iMH6DOkLA1xU1ehT5Ua7+QoBCEBgNgEE+tnIpl1giXpEjA+F+bFtszVatDoS9361Z/PjLUOdTm2oXh3edprzBfqEmD/6UCCowKDwfas6A4rgktrfoePDda3r9ameDT9jp4Jru+0gZHo59QAmwShRd/szwP7IyTtiMYAwizCLMIswy6un7CFdrol07ok69vmLB8WA69+17T75noeHjaM0vOPz0gQUD9xvee435TT41nwVb9/edJoD19PEZi7am7M21vcQ6N0PyQ6K5e0cPKy/E/PDH2VNLNb3gn/6nJbBq7N6PlhJHxaGQB/SYBsCECiYAAJ9psZRR+wHJiMi/ZTjsjXF1WQHPiD6binQa9W66qLPVviua9c9r9+hDx9vOuoJg4PaRiyczxToJ5STQ6D38cIKehMz4MHESpNAhC2EPfIB+YB8wIMPxUAqH/h9UwbTnHN6Ai4WwhgJtxlPMJ7IEQ/e5pd3Vnd+r0V5/XmyM6+5cmeOPShQD9gaPL+138oLsuFewxO+iF77034KhXvnvmMztEDP16l3zjTbKmN41f/Qwrt59r3/7mE7/0EAAhBYSIBMshDg0OWWqEfE+bFV8+ExszVUWLi/6cA6T9jbHjQ8s/kV9bbTTAvXA69k8eXEIndtPhb+6+/RuclV5IF7zfHwffDB0fadcfa++KEOtnOV/5KuZ9MR91Yj1HbbQc70cnII9GMTTx1jYsHEwuUM4gGhSjFAPHA/KBboH+gfrpoPZo2l+0NH/qV0WQAAIABJREFU9pyMgOLhqveD+gTqv834QPE2ehu5ua9/p3p01ruZe9qcV69b7f4OnL/Kzo3m3T2Buy5DYn5vvq3z4x+b1StZO/sb/1Jz6Lt7ENZqDVHNmq9T5tb9c+R7O0cPrPtV9cH3pj79c/t266sQ6AN6bEIAAhsSQKDPBNs64kig9wOhaF8sxoff3bbZmuBrLD7HYnlrItEhNZ1XrOerA+zsn9zRJcpxTnwS6G0FQDTAaCvQrBDQ8SGBPbig2YwZ1buHrq/9bzv0ofP65eQQ6H38sILexGd4bDOxYCJXi/1njLfXH66P+Vf1/Bvh8oztq3sXYZ74Jr6bFdOJ4Rq7rkfA3Q/hPRFunzVfqq8/a/1K7+98jI3darY4zb2utn6H++Oh98/HYnwzv3Zx7N7j7t/7PnSuK1SCc2v77sXze1V/RiK6n+fr2M0/OHBl6DU27by4rpBW+N8fz+r1elXPZ3tuR6D3dbxXOu8VvObGdIYp5/hiWwbO3vP1qpy9Z8Os4+Nk3UINJF4RFx2OPi2fRPv5CgEIQGAuAQT6ucQmnm+JekSMj4X4oe9mKyzbdzRRp9F0Pp0/EVNnb72eMzLU6TQdXfAEXOK886FjQmXdugOG/mr5VFlBh6oXznk/w/pE13067qv1rAcOHUebP8UL9i0T6NuHCx3OeqAQlDNPoG/qG7APm9tigHfQe3He8Sh9II5/rGBXDBQbr3//2yZb8tV9Fusv+Y/8R3xyf37Z/9s4KhxcsX1ZAoqHS/R36uv/+C/548v8oTHSt/GiePt4w71fXmCWEO6uq1fVh6+OkZV38txn5zUzOtdNVF/V8x6I+M1q/eRiPj/PrxfBvTtiu/tR12FfVM/brX7dTd/2u3o97jb29OffH1XX5ynnqF4Tz210i45o7000mkQ4f/f7Ix1CxQ18qt4Dh9kNAQhAYDIBBPrJqOadqETtPoeEd62O/3RctnoeBCK5zul3PO6qVhDXee0PyUZWJeg3K0u8CN3s6/RdvmwnqKsD00p/rWgP7abOqfeF/oYPA2o/Q8G+feed1SH5J3OJunYcl53Yz8bHnkBe2wv9rGv2uZx5An0g/Hv2Xf/aOiNMa5CMkIiQ6u6LS8aDJtuD9f9v9Why+PvDX9zcbr9Xry+E7/d//uUn+vf//LI2uGx7fMGP/EX+4n7ZPn975uHwlO3LEnCxEN6D4XYx+Vl9/aCw3vT1v/27U5fY//ov5W7W18fHx76rry+Sz4fxjauX/pXgv/fhsnfcuSvu2pb2PXcbUzsIbEUAgT4TaUvUuVbQZ/Ibs2USsHhCCGIFKStIRyeiYxPNkiZq8uVbf/3qqj/+O3g/eIH+t39XTqD3k4Z4otpM/B9/DRyPz4++a9LuBPqk/ej8pfXl+rKEBtqD9lAMHOX+t3FUmcO8w3ilxTT9hSuHqYJ3VPFQdPz+XQvvt6avd/dc1996Rfyt6ev7x+vz3XjB9fVDx3UvDx13ZephfLf82B++D/Fx+/2xY90meDuRAO07ERSnQQACHwkg0H9E9N0Jlqgjgd53ztG+cAV96rjZ+s4VrjoBAcWAjw+Er6JWxHya2HAcIUsxsNr9q1V1K6ygl2/uczX/mhyFve1XCNOe5BvFAPdf//7zTE4wJtyzCmcT6Iu+X9TXL1xBT/9exviG/LNn5spbtmtb2jcvY6xD4CoEEOgztbQl6hExPhTmx7bNViZfMVs+AYsBhK+vVwBpEsZEpYyJCu2xTEhcvIKeB3086KM/oT+50IM5G0eVP+SLPGxeqRi9rjE6ia8zCSge3Gex45GVVtAXWz/yz8yo5fRSCSiflOoffkEAAschgECfqa2UqP3ALyHSv3/dqvuP+mmrzn382X9fvY55O5l8xWz5BDpxgLBmkyl/X8ADHlcTGrWqblBYGHsH/a/q9ce/Oj/Qdf/t9+r1d/Tg5q/f/Wog92fx7nzloGfzZ/JVc1x/9q4HX6///B7Z/re997a+X39VQ+d07+f61TnhD6W544+/Eu+8b3xxx99/dct/8I588sPV8gP19THfzSd1fvP7yh/yRR4i0EdAVvnqYiGMkXBb/dnuwrb6+i9X0A/19Z36Bf1n29fXfb6vf3C85ZHun/V7NrI/1NfreG2vHhOoPfznb0H5YT5rfNGr+drxwcD5zbXd8r5/1U/t7/fX+xhbJXoxUhoBxW9pfuEPBCBwPAII9JnazBJ1Spz/sx4UOoH++etWvX7dqkcj1t9HRPpMrmL2AAQsnsKBamEDz6UDV65ftqIaftfi990K+l/V87em//nj39Xrr/96sbzOL/+qnn8HE89gUu6O3//4vXr89q/KCfTueyjQ++//c0J++9BZtu/RRFvn3KPyVbaLY2dPft6a6x/RQ4U43t01Otdtfzo/vp7v17p/aO/rtbfPES53bfZfI6w3QrDPS6+g8Pezfph5f1bvzu57dbvdq+e7qvQ6Gflef9bH2ks+lONOfD2q2+1RueJfjzZPq5zWltt6V897eE59nZ3jbd2q/oL++DpnI7p2ti9W6uobIdNi88HXK+jV19fCtfXHTSzG/W3Loj5ffb3jomN6GO++h/24/+4ezLvxQfCgX+f4481YIx4PVP+rhX5fxm//qh5/1AsDJLzf4wcTGpc04wK3uMBda+cX/Js4vo6b5p/VbxkMjhCgfUfgcAgCEJhFYMuR6izHjn6yJepIoHf7q39u1fuf/mp5/6N+bgVg4hp/3dGh4P/XBBRPPg4Q5lkRyoOawRWSxU601/xTbq2q80L0735Sq4mt+wzFafcjsWKiPNL7sbjAns6VAH+7RcK97DUTZU3abaL94cfqvPA+9uO1//t/lX6ANpXv6n6yKwS0vt7sIYOEBT9x/1Ce6pwqT8dkj+/deIIHPBQDR7h/vI9fj8RmXCjxPVSxG2E7/HFVCfB2WnNdeE5Vjaygn1hOLdDXontrW4J6V0T3An740MCVEX5PCvSNj+F59jAgeqDQXO/a4pMvM4jPPtWVH8ZsuF1MvlffbA+q4/6++Wu43+ofk9W9qD5Ufb3VR/ZC4Vuit3sw3jykt/Ndfx8cr+1L/L/5H6FXmV1+jfD+YTwgP92P4Havb378Nh5/mC/Rink9yPhQnnzt1G/D8bSv4+xI5YIjEHBtS/seoaXwEQLlE0Cgz9RGlqgjsX3sXfPPZhX9K7rGbGXyFbPlE7AY2HAgufdAlvIRfhQDftArYXhNofvA95NWjCk3JD87wnQzqW5WnL3//lXpn7v24VbWh+cHAnySf++4Ju3RxLnTXjrnVj1Tr6rx7aEVdb9Hr8ap7wdN6NsHA+kVfnXstOXFf3qv2HKfyfoRb50HO/AiHysGjnq/OL+97xsM+epV6l3h2xXbE79ttbo7txHMI5F7TKCfXE5SVNfK+nA1/MjDAHFL2Bryw3wP65S43pse2q9yV/5UPBQdzxKem9gNfe5sR8J0/SDcvbqu7k/V17//boTv6HxnS31qikd8vP4LN/cXdbV95Ya2P1XfO208kOqf1dd3/AnGHSqzPq7y6hX1Otb6s3/+dn56X1eOY8yVQYD2LaMd8AICZyCAQJ+pFZWofWccCe4S6d176N3xx8/6nwSXUKDv2MnkK2bLJ9CJA4QjhKMDC8slTpzkk8/XR7i/tArO/UVW0t/UO+i1Iq3ud8KcEm7bivvBiXAz0R047oV+NxFtVvyZPQnhf/+7fhjQTFYf//mvrcKr+Te+RysCbaLdlNtZcad9CR61kFCL/YdpX+5vH9e019D9Xd+D8JnPxzPLPuQbFrnrFfORcK9V8D4nRqvNva9D9ob269U4QTle/E7YTqzYr8X2W3WzZf0RsJ6QPuyHu7In3s/wJSp51a8uFsJ7KNy2/ibZv254/6mv760w14PlVH/Z9v+qY+8z7F9H+k8/vkgdDx8cuFfT/CdeAV/792k84P8iLlwYEPH2fv/x37Y/aHxxDxO67TX+YL+U9vQ+rxrFGCuFgO6xUvzBDwhA4LgEEOgztZ0l6pQ4734gthkY6rzwMxTonZivY5lcxewBCFgMINy0A/VoIO8nEvCBj4Tgk8eH70PCiWtU3/7EtzuRb1fUBSvswvtncCLcCAMfjtvE/JZeQff+qyvUt39an17hZ/e3xIKm7pp4uxzZXwGoVXU3W42v883eReKF+u6/glJt4GJV2+6T79vwsHFU9jFfI1gPjvMD4bzxZVwUHxLAZ5QzUxTXq3dqZpG/JxPoi77/JIRH/V2bP9L9pfr//gr6pr+PxguOQb//bB9EDB13/XgdI26uGr16LhhPpMcD7YOE3oN8d636+jBfBuMOMajbT309K+izpzcKSBLQfZA8yE4IQAACMwgg0M+ANedUS9SRQO/261U2j1/d99BrPwL9HNLXOFfx5D41KGVij7BBPFz0ftCqusF8kJr4zlxhNjgRboTOT8cb4dHnrpEHCW9Nwm2F4PhEW3/23llBJxsJHqygR5hWn0m+vGi+DIRCHwPZh41DgvpAwY3gfb+7H4cNXzej84fsDe3XdcHnTIHerrTV/YFIfzKBvuj8oL7e+sc4n3cfvNd1UR868cH0SP/p7X067n43RucMPkiox+vxeOBT/+zO7zw4aMrp9P/+/p45vtnpweg2+cfuXjY2JOBj241B+Q8CEIDAQgJkkoUAhy63RB0J9G5FvF/Z8KP/Y7AP3kE/hPPy+y2egommJhXu0w/6mmN8hwfxcH4hav4K+vEfX638O+nbFXNavdafCDf31+BEObz/2gcFw/mqWQEYTexdDHcm5i6//d3aa1fc1+Ulz//fTKGC/Mpf4NCfnnY84XKE7xuzjyiH3iWfKrgR2f072tM/2mrvce+9cmZGOd8K9JVelxO8Hqcn0CdeY2NVTTxEWOCLmV1hQ/HgY6LU8fOXK+iTD7KD/u0d/RisY9Drb4PzPx2v/tf0zYMPEtzYou2/NR54/VHfkyrb5i/W10d/gReMO2Sjbj/19aygX+HWwMQXBFwc+lj84lougQAEIBASQKAPaay4rUTtk3Uk0r9+NgOS5vP5Z/eVN+EK+o6dFf3D1LEIdOKg1IkEwsZphY3uRChewcX3zfloVV1ixXjtSzsRjv903D8gdpPxP+o/TX/99e/q+Uc9Cfb9lfLL4ES4ae/4eCMkOLuvv/5bObvKW4+/6mvc9/vtX75sd477rj99d+e05bf+u3fZP/74vXoEPmoyb+c3vtj3QFj4tEJPbec+U9dznPtbMUB8HP/Bp2/DLYZ/Wnkeier+1THBvvrVNoH4nbxuRIhPnt+I6kE51VRR3NsLVsvrh2tvwb6EQF8l/Rh44DDVl8zt5GIhvKfD7WL6A/X1g8J301eG75T3/V/z4Lvp659Nf6u+3vWhVt+R/tPnvvi496keM6ivD/txf83E8UAo2jt/hvp6a49g3GH++/qygj7z7YL5DwRcPPqY/HAehyEAAQh8IoBA/4nQl8ctUUfivH4g9tmI8zrPve5Gwn0o0PMO+i8b4GSXKU78wBchqZ1YBEKc2NhAvjnGd4RHP2g+WTx8s4K+vkfqiWz8OyjPv37Z67M8r8GJcBNPveO/qtcf/+r+vspvv1fObsu/Pkf5zH/+NrTi7Zd/cBD6ee/Za4V/Z6sn3LOCnhXx9JfB/dfeL1fsL5V3thseNqvHG+HGl98TzW/V/fnuuKT3v4enmgDubQWCvr/yQznunBmiuMoXr1sozputkVfxhPX1fxnQqd4sX6IrV/3a1q/gB09frqBXX+/65LCet4H+1p3T7z/bfBEfH+rr2/H2lPFAa989OEj19a29+tzwL/uUw5xvlfX1Q+OJ5vod+wO1w6pBjLFiCNC+xTQFjkDg8AQQ6DM1oSXqSKD3A4lon0R7ifHhd+3z12Xy9QpmNeGIJ0JHqbviycfByYRGDbJ7A/EdB9LyCd4FT1yJD4S3wb8gaCf+upfJLzyoI5+Tz30MHGXgh59ZCbhYCHNCuE1/QX+RIx68zaxRjfG9CLi2pX33ok+5EDgXAQT6TO1piXpEjI+F+KHvZiuTr1cwexaBXmKTHwQg1HdX/MIDHk0McH8gxClXIrQgtJAPyAfKAz4WrjDopY4fCbhY0D/6i/1XmKsNzpqvLdY+RiYnHHHOTvsStxCAwFoEEOjXIhnZUaL2A40RkX7KcdmKiij8a+KHoQr3uGT3FAM+XhCiEaIRonl1B39B0Fn9KAFOk3y+I8zTXyLMx/nAx0TJgz1824yAxtWKEfIF+UKxkGv8UEb+aebnqddPbXb3jReEQD/Oh6MQgMC5CSDQZ2pfG/iNiPNDK+bj/WYrk695zCLQr8nVYgBhFmEWYRZhlle72EO6XBPp3BN17LNiUzHgRRsevNs9nYuHjaPWHJxh67AEFA+54o37m1fNuRhQfCne9r9hyhfo92c034Ny2ne+71wBAQiURQCBPlN7WKKOBHrfUUf7QkE+ddxsZfK1a7bpuIM//Uz+UFX05L1+2l3/cJWefMvv+vPzj1p1ynFO+R+1elQvv9n+KertFttyJ7+r5z08p77O6uZtpX7UKr7O2Yiune2LlbraRshSg/5w4Kd97jxtc7wdGIsJfIgPxQL3B/cH+YB8QD641oMSf8+vNjLD0JEJuFgI+4Bwm/EB44Mc8eBt7n7TINDnaALXtmW0b47aYRMCENiSAAJ9JtqWqEfE+FCYH9s2W5l8NbPvZ3V3HUyolDfCdvjjqhLg7bTmuvCcqhpZQT+xnFqgrzu81rYE9a6I/nrcqlv40MCVEX5PCvTpQYq3FT8EaK53bfHJF+O54obFACvoWUEfrMiRuOTiQ9tMLJlYEg/cD+SDawnPtPfn9rZx1IpjM0wdl4Digf6S/nKL/Kl4m37HvKvX417Pyxvx935/VK93ZCGY375fj+D8e/V4dk+u57f1vFr++E+b0Ee23dcx+3Lm/awetkiuX25t9V15/+w858fAuU2Z7XzbWXhXr2dYv5uf57tFfN3/+ufd7vfqIV/Dk8fqFrELL0tti2fqGPsgAAEIzCGAQD+H1oxzlajd5yfx/dNx2ZpR/Fen1h13V/h2hnrit61Wd+c2gnkohvvShwX6yeUEHWenQr39w2XZdb1rmnqlVsvr4UJYp8T1dTUf/on52NjGfFiwoRjw8cSfwpsYDQ8mVltMrFQG8Ua8KRbcJ/FAPBAPn4VxMSrhfvE+LBiLcel5CLhYCGMy3Ca/07/liAdvc9ItpMVo9+r+eFav1ysQp6O/Im/mp06EdvadiP8IhP2OyP1+Va9Xsxjv/qiezq7719Xxux7G9h+1fVeWL+9Rl3vz5bYCeqdcJ68/W//qcltRPz5XDwXC/Xq40OFxj1hIk3C+OVG+8dUvPnRs4sl6XLcxdl0qvW/i0TvADghAAAIzCSDQzwQ29XRL1IdZQT8sctedaiTcaxW876DjDtJRGrI3tF+dd1CO7zgTthMr9tVxd1b/h43VdMJt3zzsh/fercgPxfsZvoTFrrVt8cQKelbQIwx2JtVMpJlIu/woEZB4IB6IB+6HVD6wcdRaAzPsHJqA4oF8Qb5I5QvtWys+FG9TbhqJ2e2ctblKc+/wgETm+C+/dW642Mybaea/vf0Dng3Yl4+uXqGQXg2V+35V796DgAFfmjJbu0OLAbs+m08hn7DOMaOBug3WoVtc59uc9u1cyBcIQAACEQEE+gjIWl8tUUcCvdv/acV8fNxsreVc0k7TSTZPxFVm+xkI583146L4kAA+oxzfcU4T6J1L1jH7OkT+Np1w22cP+VdXrrfKf6YvScQLdrbtwEBag2b36bjw/VgrGGkv2ksxwP1L/lIsuE/igXjIHQ8+xhaMxbj0PARcLIQ5J9wmH5GPc8SDt/nxFpIY7V5n867enX+v+lUyobjezG9bMVsFaBV+NB/WArrQhi5JfQ7ZlxDfTqybq4fKTRkfOLdXps67V8/B5f46J65vXa40gg6nXjnycdyWzgo/XdtOa9/wKrYhAAEI9Akg0PeZrLLHEnUk0Mfi+5TvZmsVz4aMjAvWvavUqTV/UtfrnzUA6B2YUY4vY7pAbz5q0NBbAR/+SOy4H6UK9Jq8+kEAr7oxcR4eCDu6N5hYM7EmH5APyAc8CFQMKB+4T79tg0U2rkxA8aD4iOOF73UOgc86/ani7fM918xPm3yl6zqfobiu+XjvnelDInNjP7Qx5tSg/aF59FC5rhD3Hvpn9fSvnnGvytErcSJRPVVm+J579/qap3vJbvjfh3o1Njt/aZ8qx5scq0NYZrut9mn3sAUBCEDgOwII9N9x+3iVErX7HBPhpxyXrY+FLjqh6YwmddhhJzjUiX3ouKeU4zvOLwR6W00fXNt0wuHzgp4Ib/wSvi/wxcwu2FAM+HhBmEeY51VHPga4H9aZOCJEIES4GOB+4n5SLjhrPPgYXzAW49LzEHCxEOa8cPus8X/2+7v0+k3LP+0cu7+CvllRH96Gs0Xm1n5X4A6NBtuD9hNzZX/ZgC7Q+QHb+t7TPdh5payzMVhm5QX+8Adp2+cSH+rV2ESgD9qWTQhAoEgCCPSZmkWdzpg4P/WY2crkq5nVyvNQxZbYHeyrhe1A/E5eNyL4J89vXlETlFN30EE5crS53v5MzX8Pn74nBgdNxxyat3fMdXdWT/8L86E9DRYm+CIfV/60GECYRZhFSOtMqplII6y6/Fj6xBz/WNGtGCBe97lfbRy18vgMc8ckoHjgftznfrxaPlS8fb5bEnPYsYsGxewhOx+E7LisQftzBHr5cq8enVfUaH9qzh292z7y690T3AdsNdfxipsIIF8hAIFiCSDQZ2oa64ijV9z4gWC0LxTqU8fNViZfu2abDjf807pQwB7oqNXxhaeaAO5txeL2h3KcU76s+Dr/xKByv8huAr0eIoQ+h6+3MVvhK25U64QfqdX9M3yR5TU/FQM+PlhBb2IcPJhYaZLnPokH4oF4QAhXDJAPyAeKBfUPPibWHJxh67AEXCyEOSLcVrzE8cN3+hfFwDfx4q+ZcMdoTh3Oc+0y/056+zay2nxIsB7aH9gMNwfm/dXgq2xT9pu5dm9+3bxTf2DOnqy/+dbYDISHegFhVx/wp7811480hcG6pepgBSc3XNtObd+kAXZCAAIQaAgg0GcKBUvUI2J8KMyPbZutTL5itnwCFgOsoGcFPUJ0Z1LNRJoHE35SxINLHlzSP9I/jvSPNo4qf8h3Lg8bESzQ0Yqon+KB/oMHeRLdc44nFW/Tgl+C8q26P57V8/WqXv7d7Xc//u0I11+IzBKyb3f3Hvh7dR+7OQft9wXyum5pcVtluvq8Xq/q+dT7552w/WEFvf9Leednfa1jodfcdF1vud3ce+r9u+5rZo5/h5tzdrBu6TqMtd289h2zxDEIQODqBBDoM0WAErX7/CS+fzouW5lcxewBCCgGfDwhRCFEIUQhRI0IUZpski8QHhQLOYUHlUG8EW+KhVLjzcfoAcZ853FxSMTbv4YuFsKcFW6XGr+l31/4N/4XBvPyz7t6OfE8/Ovw+6N6dl4R863IrJXr9T3QE67D23NQxB66t4fE7Xf1fLRi+e1Wv+6mFu4/CPTVRBbe77qckNs9xc2dO1i3oTqEYLrblk+6u/kGAQhAYDYBBPrZyKZdYImaFfTTgHHWKAGLJ4RZhFmE2c6kmok0K+j9pJcHlzy4pH+kfxzpH20cNTra4mBLYEiAa8/4tOVf1dF7rcWnq7Y5rnig/+DB4hYPFhRv20Q3pWxNgPbdmjjlQeC8BBDoM7WtJepIoPcDwWhfuII+ddxsZfIVs+UTUAz4+ECIQohCiEKIGhGiNNkkXyA8KBZ4kMWDLPIB7wieN9pdLtDPK2/bszWuVo7k/qC/VCzk6i99jG0b5pS2EQHLJxuVRzEQgMB5CSDQZ2pbS9QjYnwozI9tm61MvmK2fAIWAwizCLMIs6ygd69O40GdMXD5ER7jf1oPH/goBq56v9g4qqghXyOCB6+x6LxT2b97+VbdolXo9Y9IRj94qB9tHLLl6u1f6VC/TkLvhK65dG3pRyrFLD6nPu7sBP53HA/2N/50DhfQBmHddG+4T7ef7+RLxcBa8aB4KyD0cSEDAdo3A1RMQuCiBBDoMzW8ErXv2EdE+inHZSuTq5g9AAHFgI8XhDmbPMGDiaQmUUysERbIB+QD8gHCmmIglQ/8vlLGfBLfQ+U68U5kieV2WnNd573RE23pncuOQ3v90PuWh1fQyydnx/wS16m+6PydPp3vPh5Y+OLH1CELxlN5xlOe8U7xTrF5CVg+yVsM1iEAgQsQQKDP1MiWqGNx/lc9IHz8ulXvX7fOj788/kz/oKzZyuQrZssnYDHARIKJBCu8OpNqJpJ5JpISueALX9f/EA8I34qBo8aDjaMKGfIlfxzRL3KPV8yHAnqzHa2on2yreQDQE9WT+z8L9K3I30Kd7Et7yS5bioejxvPR78er+a942yXYKTQ7Ado3O2IKgMBlCCDQZ2pqS9SRQK/9tx/NL6f/uFWPn12hPn7dja7J5CpmD0BAMeA+Nah1n3yHB/GAcKYYIB+QDxQL9A/0j+SDfj7wTIoY830Sv+vX0JirWpXuV313X0dT6TUzPdW9qtpX0TSWvBAfX1+5E/2Coa7g/snHhJ05vljl9tlwsRDeI+E2+ZP8mSMevM19wp1SMxNwbUv7ZoaMeQhchAACfaaGtkQdCfRVs4LeHX/+E6yY/6cR6X/cqnd0jdnK5CtmyydgMcAKelbQ82CmM6lmIs1E2uVHhGkeVCkGiAfuB8VC2D/YOKqIIV8jfjeijnxrPyOBXivr3fk9IX6Gra0E+hn12qs5WtbcL6n7RfscJ22H95P2cXwaH8XbXvFOuXkJ0L55+WIdAlcigECfqbWVqP3AJRTcG4H+3rzOJjz+bFbVv4LzO3Yy+YrZ8gl04oB30Ntkwd8/8IAHD658DHA/TJsoIyzUYj7xQrzoXriK8OZjvogh3/Dq9KRw7aX/AAAgAElEQVR7zSto7ve7f0Dd1ehn2NpKoO86mKzS3jtdLIQ5MNy+yv1wtft/7/qWk3/2vvvOV77lk/NVjRpBAAIbE0CgzwTcEnUgtvtX10QCffg6m5RA746brUy+YrZ8AhYDCJEIkayg70yqmUizgt7lx70n3pTPCn7FAPFY5v1o46gihnzpd8mnXWsEeP/e+fB99Dp7hq3sAv0MX+T+Tp+KB+7XMu/Xs+VTxdtO4U6xmQnQvpkBYx4CFyKAQJ+psS1RRwK99msFPQJ9pgY4mVnFjfvUoNV98h0exAPCoGKAfEA+UCzQP9A/kg/6+cAzKWV8qPfKR6vN/Xvjg331j64G73tPXZfa518tf+++EmeWQD8sttfvtg98CplO9SW8ZodtFwvhPRJukz/JnzniwdvcIdYpMj8B17a0b37OlACBKxBAoM/UypaoI4Fe76BHoM8E/qRmLZ5YQc8Keh7MdCbVTKSZSPtJEa+6soe38OgLszy44EGmjaOKGicm3h8fiPOVXm3zfHe8rgXyWxWeaj8WG77/vXtCVdtLCOuNqN79kdj2x2Nrdu11owK99/RDvTq12eeL4oF8Sb7con9QvO0T7ZSamwDtm5sw9iFwHQII9JnaWonaD/xCkT56xU14PPWKm46dTL5itnwCnThAiEKI4kEND2p4UMODGv6iyvoCHtTxoM6Ppz+Mj/w55Q/58HADAhpXS5ydEj86l3xDvvkmXsg/G9zYOxVh+WSn8ikWAhA4DwEE+kxtaYk6FOfddiTQ84qbTA1wMrMWTwizCLMIswizCLMIsx+ESIQkVowrBrwoRLz4fsOzONn4kOp8R0Djau4PVtArV+Z88KJ4+y5auap0ArRv6S2EfxA4DgEE+kxtZYk6Eui1n1fcZAJ/UrOKG/e5xUBSZVAevBULOScuKoN4I94UC8QbKxTJB+SDtfOBj6mTjhOp1jwCLhbCHBNu0//Q/+SIB29zXphy9kEIuLalfQ/SWLgJgcIJINBnaiBL1JFAH66Yn7pttjL5itnyCVgMsIKeFfSsoO9MqplIM5H2kyJWCNvDW3ggbK8tbJ/Bno2jyh/y4eEGBBQP5Evy5Rb5TfG2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuB34hIP+W4bGVyFbMHIKAY8PGCEIUQxYMaHtTwoIYHNfxFlfUFPKjjQd2U8ZE/5wBjPlzMT0DjaomzU+JH55JvyDffxAv5J/99vVcJlk/2coByIQCB0xBAoM/UlJaoR8R5VtBngn9CsxZPCLMIswizCLMIswizPKi1GPCiBzzg8WF8ZOOoE44RqdJ8AooH8gcr6Ld48KJ4mx+pXHEEArTvEVoJHyFwDAII9JnayRJ1JND7gWC0LxTqU8fNViZfMVs+AcWAjw+ECISID0KEJhvECxNPxQIr/ljxRz4gH1w9H/h7oPwhHx5uQMDFQpgTw236S/rLHPHgbW4Q2xSxPQHXtrTv9twpEQJnJIBAn6lVLVGPiPGhMD+2bbYy+YrZ8glYDCDMenHeD4J4UMGDCu4H7gf+oqQjMiEsISzRP6YfxNg4qvwhHx5uQEDxwP2Svl/0MA8+6/BRvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfmAzItJPOS5bmVzF7AEIKAZ8vCBMI0wjTCNMI0wjTPOqI+sLeDDBg4kp4yN/zgHGfLiYn4DG1QjR/4/x1EbjKfJP/vt6rxIsn+zlAOVCAAKnIYBAn6kpLVGPiPNjq+bDY2Yrk6+YLZ+AxQDCLBOJjSYSmrQifCF8ufxDPNQiBvcD9wP3wzHzgY2jyh/y4eEGBBQP3M/HvJ81JjlK+yneNghtitiBAO27A3SKhMBJCSDQZ2pYS9SRQO8HEtG+WIwPv7tts5XJV8yWT0Ax4OOHFfQmFsKDiZUmaQinCKfkA/IB+YAHSYqBVD7w+8of8uHhBgRcLIQxEm4znmA8kSMevM0NYpsitifg2pb23Z47JULgjAQQ6DO1qiXqETE+FuKHvputTL5itnwCFgOsoGcFPSvoO5NqJtJMpP2kiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+DBrh7q5RxPKt42CG2K2IEA7bsDdIqEwEkJINBnalglaj/wGxHppxyXrUyuYvYABBQDPl4QohCiEKIQokaEKE02yRcID4qFnMKDyiDeiDfFQqnx5mP0AGM+XMxPwMVCmLPC7VLjt/T7C//G/4KJ/JP/vt6rBMsnezlAuRCAwGkIINBnakpL1CPi/NCK+Xi/2crkK2bLJ2AxgDCLMIsw25lUM5FmBb3LjwgD48IAfOCjGLjq/WLjqPKHfHi4AQHFw1Xvh6vng63rr3jbILQpYgcCtO8O0CkSAiclgECfqWEtUUcCvR8IRvtCQT513Gxl8hWz5RNQDPj4YAW9iXHwQJjUJMt9Eg/EA/GAEK0YIB+QDxQL6h98TJQ/5MPDDQi4WAhzRLiteInjh+/0L4qBb+LFX7NBbFPE9gRc29K+23OnRAickQACfaZWtUQ9IsaHwvzYttnK5CtmyydgMcAKelbQI0R3JtVMpHkw4SdFPLjkwSX9I/3jSP9o46jyh3x4uAEBxQP9Bw/yJLrnHE8q3jYIbYrYgQDtuwN0ioTASQkg0GdqWCVqP/AbEemnHJetTK5i9gAEFAM+XhCiEKIQohCiRoQoTTbJFwgPioWcwoPKIN6IN8VCqfHmY/QAYz5czE/AxUKYs8LtUuO39PsL/8b/woD8k/++3qsEyyd7OUC5EIDAaQgg0GdqSkvUI+L82Kr58JjZyuQrZssnYDGAMIswizDbmVQzkWYFvcuPCAPjwgB84KMYuOr9YuOo8od8eLgBAcXDVe+Hq+eDreuveNsgtCliBwK07w7QKRICJyWAQJ+pYS1RRwK9HwhG+2IxPvzuts1WJl8xWz4BxYCPH1bQmxgHD4RJTbLcJ/FAPBAPCNGKAfIB+UCxoP7Bx0T5Qz483ICAi4UwR4Tbipc4fvhO/6IY+CZe/DUbxDZFbE/AtS3tuz13SoTAGQkg0GdqVUvUI2K8E98fLqH/uFXvkfPMViZfMVs+AYsBVtCzgh4hujOpZiLNgwk/KeLBJQ8u6R/pH0f6RxtHlT/kw8MNCCge6D94kCfRPed4UvG2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuB3yfxfUSg79jJ5CtmyyfQiQOEKIQohCiEqBEhSpNN3/+QL8gX5AvyBfnCP9j1ObH8IR8ebkBA42r6y3pVPOOF/A8qyD8b3Ng7FWH5ZKfyKRYCEDgPAQT6TG1piXpEnGcFfSb4JzRr8YTQgtCC0MIKet65bqJ7zhVvCDcIN8TXef5Cx8ZRJxwjUqX5BBQP7lO5nvv9PPe72rSU9lW8zY9UrjgCAdr3CK2EjxA4BgEE+kztZIk6Euj9QOH/btXrZ/tueZ2rT95Bn6lRDmxWseHjhxWxNpmCBxNLTcKYWDOxJh+QD8gHvCNaMZDKB37fgceCuL4eARcLYYyE24wnGE/kiAdvc70QxlJBBFzb0r4FNQiuQODABBDoMzWeJepIoDfx/Z9b9fp1q+7NO+ifv+rvr39ulZ3TXGu2MvmK2fIJWAywgp4V9Kyg70yqmUgzkfaTIh5c8uCS/pH+caR/tHFU+UM+PNyAgOKB/oMHu3qol3M8qXjbILQpYgcCtO8O0CkSAiclgECfqWGVqP3Ab0ik/79mFT3voM/UCucx24knhCiEKIQohKgRIUqTTd//kC/IF+QL8gX5wj/Y9TnxPENDarKAgMbV9Je8yiynMB/GF/lnwQ1b+KWWTwr3E/cgAIHyCSDQZ2ojS9Qj4jzvoM8E/4RmLZ4QWhBaEFpYQc87c01032pirUk25fEXG15k4cGX3YNH4WHjqBOOEanSfAKKh6PEr/og/D3min/F2/xI5YojEKB9j9BK+AiBYxBAoM/UTpaoI4HeD6yCfY/mFTfvZl983In4ZiuTr5gtn4BiwMcHwsDhhAEmVqzQQthF2CV/H1NYIX+fJ3/7e7D8IR8ebkBA42ru7/Pc32rLUsdb5J8NbuydirB8slP5FAsBCJyHAAJ9pra0RB2I8fG75VlBnwn+Cc1aPLGCnhX0rKBnBT0r6O0hXakT8dKFAvyrRSni5zoPzmwcdcIxIlWaT0Dx4D7Jh+RDxUCueFC8zY9UrjgCAdr3CK2EjxA4BgEE+kztpETtO/oRkd6fxzvoM7XCecx24okV9DaZ8vcXPODBgysfA9wPCC0SGRCeryM8q825/z/f/57ReYaG1GQBARcL4T0TbpM/yZ854sHbXBCzXFouAde2tG+57YNnEDgSAQT6TK1liXpEnHcr6J8/6oT+GjnPbGXyFbPlE7AYQIhEiGQFfWdSzUSaibSfFPGgjgd19I/0jyP9o42jyh/y4eEGBBQP9B+fH2zpISDjre/HW4q3DUKbInYgQPvuAJ0iIXBSAgj0mRrWEnUkvPuBYLDv9bN5x/yPW/VotuNX4ZitTL5itnwCigEfPwhRCFEIUQhRI0KUJtPkC4QHxQLCyvfCihhyPx3/fvJtWP6QDw83IOBiIbynw23yJfkyRzx4mxvENkVsT8C1Le27PXdKhMAZCSDQZ2pVS9SBGB8L7/r+aFbRu2vuf94q7den2crkK2bLJ2AxgDCLMIsw25lUM5FmIu3yo0RU4oF4IB64H1L5wMZR5Q/58HADAooH8gX5IpUvtG+t+FC8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStS+Yx8R6accl61MrmL2AAQUAz5eWEFvYhw8mFhpEuU+iQfigXjgx/4UA+QD8oFiQf2Dj4kDjPlwMT8BFwthjgi3FS9x/PCd/kUx8E28+GvyhzYl7EDAtS3tuwN4ioTACQkg0GdqVEvUI+K8Vsh/+jRbmXzFbPkELAZYQc8KeoTozqSaiTQPJvykiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+BBnkT3nONJxdsGoU0ROxCgfXeATpEQOCkBBPpMDWuJOhLo/UAw2hcK9KnjZiuTr5gtn4BiwMcHQhRCFEIUQtSIEKXJJvkC4UGxkFN4UBnEG/GmWCg13nyMlj/kw8MNCLhYCHNWuF1q/JZ+f+Hf+F8YkH82uLF3KsLyyU7lUywEIHAeAgj0mdrSEvWIGB8K82PbZiuTr5gtn4DFAMIswizCbGdSzUSaFfQuPyIMjAsD8IGPYuCq94uNo8of8uHhBgQUD1e9H66eD7auv+Jtg9CmiB0I0L47QKdICJyUAAJ9poZVovYDvxGRfspx2crkKmYPQEAx4OOFFfQmxsEDYVKTLPdJPBAPxANCtGKAfEA+UCyof/AxcYAxHy7mJ+BiIcwR4bbiJY4fvtO/KAa+iRd/Tf7QpoQdCLi2pX13AE+REDghAQT6TI1qiXpEnB9bNR8eM1uZfMVs+QQsBlhBzwp6hOjOpJqJNA8m/KSIB5c8uKR/pH8c6R9tHFX+kA8PNyCgeKD/4EGeRPec40nF2wahTRE7EKB9d4BOkRA4KQEE+kwNa4k6Euj9QDDaF4vx4Xe3bbYy+YrZ8gkoBnz8IEQhRCFEIUSNCFGabJIvEB4UCzmFB5VBvBFvioVS483HaPlDPjzcgICLhTBnhdulxm/p9xf+jf+FAflngxt7pyIsn+xUPsVCAALnIYBAn6ktLVGPiPGxED/03Wxl8hWz5ROwGECYRZhFmO1MqplIs4Le5UeEgXFhAD7wUQxc9X6xcVT5Qz483ICA4uGq98PV88HW9Ve8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStR+4Dci0k85LluZXMXsAQgoBny8sILexDh4IExqkuU+iQfigXhAiFYMkA/IB4oF9Q8+Jg4w5sPF/ARcLIQ5ItxWvMTxw3f6F8XAN/Hir8kf2pSwAwHXtrTvDuApEgInJIBAn6lRLVGPiPNDK+bj/WYrk6+YLZ+AxQAr6FlBjxDdmVQzkebBhJ8U8eCSB5f0j/SPI/2jjaPKH/Lh4QYEFA/0HzzIk+ieczypeNsgtCliBwK07w7QKRICJyWAQJ+pYS1RRwK9HwhG+0JBPnXcbGXyFbPlE1AM+PhAiEKIQohCiBoRojTZJF8gPCgWcgoPKoN4I94UC6XGm4/R8od8eLgBARcLYc4Kt0uN39LvL/wb/wsD8s8GN/ZORVg+2al8ioUABM5DAIE+U1taoh4R40NhfmzbbGXyFbPlE7AYQJhFmEWY7UyqmUizgt7lR4SBcWEAPvBRDFz1frFxVPlDPjzcgIDi4ar3w9Xzwdb1V7xtENoUsQMB2ncH6BQJgZMSQKDP1LBK1H7gNyLSTzkuW5lcxewBCCgGfLywgt7EOHggTGqS5T6JB+KBeECIVgyQD8gHigX1Dz4mDjDmw8X8BFwshDki3Fa8xPHDd/oXxcA38eKvyR/alLADAde2tO8O4CkSAickgECfqVEtUY+I82Or5sNjZiuTr5gtn4DFACvoWUGPEN2ZVDOR5sGEnxTx4JIHl/SP9I8j/aONo8of8uHhBgQUD/QfPMiT6J5zPKl42yC0KWIHArTvDtApEgInJYBAn6lhLVFHAr0fCEb7YjE+/O62zVYmXzFbPgHFgI8fhCiEKIQohKgRIUqTTfIFwoNiIafwoDKIN+JNsVBqvPkYLX/Ih4cbEHCxEOascLvU+C39/sK/8b8wIP9scGPvVITlk53Kp1gIQOA8BBDoM7WlJeoRMT4W4oe+m61MvmK2fAIWAwizCLMIs51JNRNpVtC7/IgwMC4MwAc+ioGr3i82jip/yIeHGxBQPFz1frh6Pti6/oq3DUKbInYgQPvuAJ0iIXBSAgj0mRpWidoP/EZE+inHZSuTq5g9AAHFgI8XVtCbGAcPhElNstwn8UA8EA8I0YoB8gH5QLGg/sHHxAHGfLiYn4CLhTBHhNuKlzh++E7/ohj4Jl78NflDmxJ2IODalvbdATxFQuCEBBDoMzWqJeoRcX5oxXy832xl8hWz5ROwGGAFPSvoEaI7k2om0jyY8JMiHlzy4JL+kf5xpH+0cVT5Qz483ICA4oH+gwd5Et1zjicVbxuENkXsQID23QE6RULgpAQQ6DM1rCXqSKD3A8FoXyjIp46brUy+YrZ8AooBHx8IUQhRCFEIUSNClCab5AuEB8VCTuFBZRBvxJtiodR48zFa/pAPDzcg4GIhzFnhdqnxW/r9hX/jf2FA/tngxt6pCMsnO5VPsRCAwHkIINBnaktL1CNifCjMj22brUy+YrZ8AhYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaOKn/Ih4cbEFA8XPV+uHo+2Lr+ircNQpsidiBA++4AnSIhcFICCPSZGlaJ2g/8RkT6KcdlK5OrmD0AAcWAjxdW0JsYBw+ESU2y3CfxQDwQDwjRigHyAflAsaD+wcfEAcZ8uJifgIuFMEeE24qXOH74Tv+iGPgmXvw1+UObEnYg4NqW9t0BPEVC4IQEbkoofNaJFQ5wIAaIgb1iYMnAX9e6T+c/35lIKgaIh/z3w145g3Lpr4gBYoAYWBYD6ivnjJ9gvow5/OBHDBADR4uBE2rBVKlAAgj0zRPPoyUI/KVTIwbOGQPfTBR1jYsJbc+ZaOoaroefYoH4mf6gi1x8zlxMu9KuxMD5Y0B93jfjH+Lj/PFBG9PGxAAxoBgoUMvFpRMS4BU3J2xUqgQBCByLAB3/sdoLbyEQEuD+DWmwDQEIQKB8Akvz9tLryyeEhxCAAAQg4AiQ74mDLQkg0G9Jm7IgAAEIJAjQ8SegsAsCByHA/XuQhsJNCEAAAg2BpXl76fU0BAQgAAEIHIMA+f4Y7XQWLxHoz9KS1AMCEDgsATr+wzYdjkOAlTXEAAQgAIGDEVg67lp6/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+Odlxei9ejcsnn/ny3tlL72qNsQQACKxGg418JJGYgsAMB7t8doF+tyNR4LLXvalyoLwS+JLA0by+9/ku3uQwC8wmk+orUvvmWuQIClyBAvr9EMxdTSQT6NZri/aoe97sXuP0NfL9Xj1cgdK9RRm4bqY46tS+3Hyez/37WcdF58HGyOlKd5QTo+JczxAIE9iLA/bsX+YnlMkabCOp6pzFGu16bq8ZL8/bS6+UHn4UToP8ouoHI4UU3z2mcI9+fpikPUREE+qXN9HpU99utXn3+eFSPR/A9XI2+tJzc16fE+NS+3H58Zf9VPVwb3J9VaY9FGDh81aCXu4iO/3JNToVPRID7t+DGZIxWQOMwRiugEXAhIrA0by+9PnKHryUSoP8osVU6PjHP7uDgSyYC5PtMYDGbJIBAn8Qyfefr4cT5exVr8a7DONSq6ZQYn9o3Hc2GZ5Y7+dsQAkUdmAAd/4EbD9cvT4D7t9wQYIxWQtswRiuhFfChS2Bp3l56fdcbvpVIgP6jxFbBJwhsT4B8vz3zK5eIQL+o9d/V8+4E+kf1WmSngItTYnxqXwGu9l1g8tdnwp4jEaDjP1Jr4SsEugS4fw+uuOcAABK7SURBVLs8yvnGGK2MtmCMVkY74EVIYGneXnp96AvbJRKg/yixVfAJAnsQIN/vQf26ZSLQL2p7dd636jFJoX9Xr8fdXonjbvb7/VH1XlffCOPO5jv48zq3Ut/ebf9+Vg//cKBewf+Il/BbveaV2Vn1PyjQT7RpPsQbE65vyu69tub9rPk1r7OpVzfUrxhS8vSfnQaZUJ5zcYx7ku+7ej3bVxrV7fnsPqwZYxhdexv67YLZfsW8+V46AcVu6X7iHwQg0CfA/dtnUsYexmiKzeRYc7CRJoyZGKO19BijtSwOtKV741uXl17/bblctxUB+g/F+OT+YywXSuyYpF+8a/3DdI4RraMps6NfVBPm5z6M+ucxF9/q/jpWOboXjuU13h6VAAL90pbTJMWJ7Y/XyDvQ1dHfq/vjWb1er0DcjV6RI5vND8/e/bvt2x+hvT+a7fund97PL7PTwQ10evVfDUyoR5LtdJ8kvodae+/PDd+v6vWSaP+ono6r+2cvo59engR61zm7ROwGJI/ggUqHjdfz6wcDnfa8p9uye618cu/Nv/vfLeiUE1bYMYzj4YNfSezsLJoAHX/RzYNzEBglwP07imffg+o/GaMlX8fYbxyNTz6P8RijNfQUYxPHjn3m7NmDwNK8vfT6PepMmTMJ6N6m/5jWf4iXcuGX+oW9V/6ueX27KLE7n27nyOF+9U2j8/NKfR1z8Zl3xSVPJ99fstl3qzQC/Qrou6vcnVD/DATiugB1NrH2WmlFeHhAHVz0bnvZcEki7IjMRvQjqTo/NO29GSmzY7fxI9w3y2aC7bzrmz+L1iuEEv7URQz/+fSs8ga4p/k2HXvEvFflhM/y6dZrGNU3LfL3futA7fjJh55T7CiNAB1/aS2CPxCYToD79/+3d2/XjcJAAEBTVwpKPa4mzaQY7wF7bCwesSIWD/h+7CEEhIYrGAnZYZ+3esWexmjn820cMxp3PLZIjE9Gu8V442FDjFmur3mcGO9cjm6MdvvOyCO3tRcKtObt1vIvPHVVVwjoP57vP25fKGucvzj/fJ9/Rklzph8Z9TvPPZ9HX+dZvOJmeONd5fs3bvwXnLoJ+tXQyz+T6l5HEwePzqJ7nc3P+efh3/flVTXDSdZRZ3M9zuQDUrctPgUevgt/hTpHcVQeM07/tvxD+WsMH92n8B/dp9ynib9SmOm0w6V/jVCDexwnPijozyfMP8+n+9f1b2d6+2HO8OFYt73PMWAYfigSA56H3z3EMGz3+7H8tB8BHf9+2kqkBEoB928pknHdGK1/LeLkGCrayxhtejwdPt3nHNe/sBy+9nA0zov9Y5xojBYimZatebu1fCYLsfwmoP/4vf+Y/jZ7L1s1fzHXFjP5dJR/Y7+l5/PYZzo3y/NzbfC+v5fv37ftX3HmJuhXV+868XgdTST++JbRxLvSu0nncuJ51NlEkNfj3Gf+rxumOpoV6hzFUXnMCPu2/Fv5+FO10TfIy+OOHjwr6xudb1Qw5Xv5RsHt/wHoXlVzmnjF0eiY15hGsV7ruu7/8In+6Bi/xBWbLXcjoOPfTVMJlMBIwP07Ikn8C2O00RcTb61VOWa6ljNG+7q8FnE4ad/bzIwdb95+eKVAa95uLf/Kc1f3XwX0H/P9x8IE/fnatzw1fxFt072H/nQ+9a/JGb7SN+ZWrvtNPSMP33M/+XzuWTyULZ8TkO+fc7LXOgIm6NdxHB0lHlgufdG9Ixh/g/76ze7hEaY6m357TQe3Qp2jOCqPOTynYfyf3SuAym+0Tzj0ZeIB5/JBxqhvL477OHCojHd0vnECEUMxKLhu7gYQt4n64s/6xt9+v8f0GOv1YNcYTNCH/Xssdfzv0c7O8pgC7t/9tasx2lSb3ccnxmhTf615n4AyRpu6fvb1u9a83Vp+X1qiHQroP4Yag59nn6OvfcvoIX7m+fr76/wZX2AcLYtn8dk6z/0E//Tz+b2v8yw+aD8/zgrI97M0NvwHARP0/wG1O+Rj5z3TAc3VPdvZ1HRwK9Q5iqPymKPzqy8ff2bWfTu9f8XN5Kth5jrayvpG5xsn8NxxuvcU9gl8OAAZHXP5WHG+D6+zGR2jLq7Y2zKvgI4/b9uIjMBvAu7f34TybTdGm2qT5fHJZInrX4waoxX/N1SPVe85Zex3/0egNW+3lv8/Z+WoWwjoP2aUZ59X/zJ/0b0qeDh9PpNPZ+u8xzh+Pp851rWIZ/G7nZ8uAvK9K2FLARP0LdrdO9X695sXB/kZTyZPJvso1n+bPFbu39B5mKTtN9d0cDPvyoxqnqlzotOrOo+oa7CsKh/vrIvXwVzjefjmUn/s+Y62qr6J872EPn/8wal1DXf5EGFxgv7+4c2ofW/XzfR/Ejvaf/Ld+I8RWduHgI5/H+0kSgJTAu7fKZUEvzNGe2yEctz3uLVfqxozGaNdBJvHjhMN4Vf/XaA1b7eW/+8nqII2Af3Ho98T/cf4r8bjEBPPx/2mqefr677x7B+H6J6xP7u/pn/+G/S3ohPP5/Ehy+jZ2rP4nc1PNwH5/kbhhw0ETNC3IMfDSf8O+cv70b6+4v3z5bdprh3Ox8f58+t0Pn1/n7/7d6vV/IdTNR1cd2KNdU4+dFQcc9L22fLRaT9OVkeHOpwD78/0K97l37XD5/nztsOz9S19MBKxDAYFfdt39ZzO39e2jD+ju1V9CWzi3aT3mD66d+P179ebu24q45o098vsAjr+7C0kPgLzAu7feZuXbjFGWx5rTjbOfXyyPFaNcZEx2vykVBgNxo6T5n75CoHWvN1a/hXnrM4KAf1Hff8xOW/QmV/7lYcH5O730zkynvXjGft0Gr7ypsinZZ3PPp9HTP0cjmfxijvjLXeV79+y2V920iboW+l/vs+nbkJ48I60y7fqh3+WFZX8nL+LfT8+v86nhz/hWpqQrevgLrU21Fl2enEa5yePedu//OH38rPf4roNmIoOuuto+0/WLxP1j5+I/15fH+HC+Z5Gn9qvcMziWuium9G10AVWFVdpbX0PAjr+PbSSGAlMC7h/p11S/NYY7fLqvbnxxWQj/T6+MUYbwBmjDTD282Nr3m4tvx+pN45U/1HXf8zmwtr5i59+biXusY+Py+tuLhP3xfP/qM7f+6/7FX2pp5zD8Sx+F/LTRSCuRR4EthAwQb+FsjoIECCwIKDjX8CxiUByAfdv8gYSHgECBAqB1rzdWr4IxyoBAgQIJBWQ75M2zEHDMkF/0IZ1WgQI7EdAx7+fthIpgVLA/VuKWCdAgEBugda83Vo+t47oCBAgQCAE5PuQsNxCwAT9FsrqIECAwIKAjn8BxyYCyQXcv8kbSHgECBAoBFrzdmv5IhyrBAgQIJBUQL5P2jAHDcsE/UEb1mkRILAfAR3/ftpKpARKAfdvKWKdAAECuQVa83Zr+dw6oiNAgACBEJDvQ8JyCwET9Fsoq4MAAQILAjr+BRybCCQXcP8mbyDhESBAoBBozdut5YtwrBIgQIBAUgH5PmnDHDQsE/QHbVinRYDAfgR0/PtpK5ESKAXcv6WIdQIECOQWaM3breVz64iOAAECBEJAvg8Jyy0ETNBvoawOAgQILAjo+BdwbCKQXMD9m7yBhEeAAIFCoDVvt5YvwrFKgAABAkkF5PukDXPQsEzQH7RhnRYBAvsR0PHvp61ESqAUcP+WItYJECCQW6A1b7eWz60jOgIECBAIAfk+JCy3EDBBv4WyOggQILAgoONfwLGJQHIB92/yBhIeAQIECoHWvN1avgjHKgECBAgkFZDvkzbMQcMyQX/QhnVaBAjsR0DHv5+2EimBUsD9W4pYJ0CAQG6B1rzdWj63jugIECBAIATk+5Cw3ELABP0WyuogQIDAgoCOfwHHJgLJBdy/yRtIeAQIECgEWvN2a/kiHKsECBAgkFRAvk/aMAcNywT9QRvWaREgsB8BHf9+2kqkBEoB928pYp0AAQK5BVrzdmv53DqiI0CAAIEQkO9DwnILARP0WyirgwABAgsCOv4FHJsIJBdw/yZvIOERIECgEGjN263li3CsEiBAgEBSAfk+acMcNCwT9AdtWKdFgMB+BHT8+2krkRIoBdy/pYh1AgQI5BZozdut5XPriI4AAQIEQkC+DwnLLQRM0G+hrA4CBAgsCOj4F3BsIpBcwP2bvIGER4AAgUKgNW+3li/CsUqAAAECSQXk+6QNc9CwTNAftGGdFgEC+xHQ8e+nrURKoBRw/5Yi1gkQIJBboDVvt5bPrSM6AgQIEAgB+T4kLLcQMEG/hbI6CBAgsCCg41/AsYlAcgH3b/IGEh4BAgQKgda83Vq+CMcqAQIECCQVkO+TNsxBwzJBf9CGdVoECOxHQMe/n7YSKYFSwP1bilgnQIBAboHWvN1aPreO6AgQIEAgBOT7kLDcQsAE/RbK6iBAgMCCgI5/AccmAskF3L/JG0h4BAgQKARa83Zr+SIcqwQIECCQVEC+T9owBw3LBP1BG9ZpESCwHwEd/37aSqQESgH3bylinQABArkFWvN2a/ncOqIjQIAAgRCQ70PCcgsBE/RbKKuDAAECCwI6/gUcmwgkF3D/Jm8g4REgQKAQaM3breWLcKwSIECAQFIB+T5pwxw0LBP0B21Yp0WAwH4EdPz7aSuREigF3L+liHUCBAjkFmjN263lc+uIjgABAgRCQL4PCcstBEzQb6GsDgIECCwI6PgXcGwikFzA/Zu8gYRHgACBQqA1b7eWL8KxSoAAAQJJBeT7pA1z0LBM0B+0YZ0WAQL7EdDx76etREqgFHD/liLWCRAgkFugNW+3ls+tIzoCBAgQCAH5PiQstxAwQb+FsjoIECCwIKDjX8CxiUByAfdv8gYSHgECBAqB1rzdWr4IxyoBAgQIJBWQ75M2zEHDMkF/0IZ1WgQI7EdAx7+fthIpgVLA/VuKWCdAgEBugda83Vo+t47oCBAgQCAE5PuQsNxCwAT9FsrqIECAwIKAjn8BxyYCyQXcv8kbSHgECBAoBFrzdmv5IhyrBAgQIJBUQL5P2jAHDcsE/UEb1mkRILAfAR3/ftpKpARKAfdvKWKdAAECuQVa83Zr+dw6oiNAgACBEJDvQ8JyCwET9Fsoq4MAAQILAjr+BRybCCQXcP8mbyDhESBAoBBozdut5YtwrBIgQIBAUgH5PmnDHDQsE/QHbVinRYDAfgR0/PtpK5ESKAXcv6WIdQIECOQWaM3breVz64iOAAECBEJAvg8Jyy0ETNBvoawOAgQILAjo+BdwbCKQXMD9m7yBhEeAAIFCoDVvt5YvwrFKgAABAkkF5PukDXPQsEzQH7RhnRYBAvsR0PHvp61ESqAUcP+WItYJECCQW6A1b7eWz60jOgIECBAIAfk+JCy3EDBBv4WyOggQILAgoONfwLGJQHIB92/yBhIeAQIECoHWvN1avgjHKgECBAgkFZDvkzbMQcMyQX/QhnVaBAjsR0DHv5+2EimBUsD9W4pYJ0CAQG6B1rzdWj63jugIECBAIATk+5Cw3ELABP0WyuogQIDAgoCOfwHHJgLJBdy/yRtIeAQIECgEWvN2a/kiHKsECBAgkFRAvk/aMAcN6yMuOMuPMwMGrgHXwCuvgYP2M06LwKEFXpkz1K3Pcg24BlwDf78G/to5Mf+7OTt2rgHXwB6vgb/2F8oRqBEwQf8hQe4xQYrZdXvEa6AmeduXAIEcAkfMRc5JH+sacA28wzXw117kHWycoxzgGnANuAbu18Bf+wvlCNQIeMVNjZZ9CRAgQIAAAQIECBAgQIAAAQIECBAgQIDASgIm6FeCdBgCBAgQIECAAAECBAgQIECAAAECBAgQIFAjYIK+Rsu+BAgQIECAAAECBAgQIECAAAECBAgQIEBgJQET9CtBOgwBAgQIECBAgAABAgQIECBAgAABAgQIEKgRMEFfo2VfAgQIECBAgAABAgQIECBAgAABAgQIECCwkoAJ+pUgHYYAAQIECBAgQIAAAQIECBAgQIAAAQIECNQImKCv0bIvAQIECBAgQIAAAQIECBAgQIAAAQIECBBYScAE/UqQDkOAAAECBAgQIECAAAECBAgQIECAAAECBGoETNDXaNmXAAECBAgQIECAAAECBAgQIECAAAECBAisJGCCfiVIhyFAgAABAgQIECBAgAABAgQIECBAgAABAjUCJuhrtOxLgAABAgQIECBAgAABAgQIECBAgAABAgRWEjBBvxKkwxAgQIAAAQIECBAgQIAAAQIECBAgQIAAgRoBE/Q1WvYlQIAAAQIECBAgQIAAAQIECBAgQIAAAQIrCZigXwnSYQgQIECAAAECBAgQIECAAAECBAgQIECAQI2ACfoaLfsSIECAAAECBAgQIECAAAECBAgQIECAAIGVBEzQrwTpMAQIECBAgAABAgQIECBAgAABAgQIECBAoEbgH6WiRri5sayzAAAAAElFTkSuQmCC[/img]
Pour répondre à tes questions je ne sais pas s'il vaut mieux déporter le mur de soubassement de la semelle pour avoir moins de déport de la dalle ou de centrer le mur de soubassement mais avoir plus de déport de la dalle. Qu'en penses tu?
Dans mes recherches, je n'ai pas trouvé de dalle solidarisée sans isolation dessous
 . Je n'ai trouvé d'hérisson que sous des dalles flottantes...
. Je n'ai trouvé d'hérisson que sous des dalles flottantes...
Je pense tout de même qu'il est intéressant de mettre un hérisson afin d'avoir de l'inertie dans le sol (ça sera une ossature bois). Mais est ce vraiment pertinent et/ou efficace?
 [img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABegAAAF1CAYAAACTcQoTAAAgAElEQVR4AeydPdKruNa2PZgTdNWegZMOO9kjOPEpRx2dCXS8M4edfVEP4CSO33l4MHwlwb0QQmAwCARcXbXbmJ+lpUuLJelGD75V/AcBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMDmBG6bl0iBEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIVAj0BAEEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0GeCfrvdKv7BgBggBogBYoAYIAaIAWKAGCAGiAFigBg4VgysJRPQ7sdqd9qL9iIGiIHdYmCtjgc7XQK7NSgPBngwQgwQA8QAMUAMEAPEADFADBADxAAxQAx8HQPd2f3339AFEPuIAWKAGCAGJsXA910NV44REPzq/27V0n9ma6xAjkEAAhCAAAQgAAEIQAACEIAABCDwNYG1595r2/u6YlwIAQhAAAJFE+AVN5maxzriSKB3+8cE+9Rxs5XJV8xCAAIQgAAEIAABCEAAAhCAAASuTmDtuffa9q7ePtQfAhCAwFkJINBnalnriCOBfkycHzpmtjL5ilkIQAACEIAABCAAAQhAAAIQgMDVCaw9917b3tXbh/pDAAIQOCsBBPpMLauO2H0OCe9u/5TjspXJVcxCAAIQgAAEIAABCEAAAhCAAAQuT2Dtuffa9i7fQACAAAQgcFICCPSZGtY6YlbQZyKMWQhAAAIQgAAEIAABCEAAAhCAwHoEbB6/ksm17a3kFmYgAAEIQKAwAgj0mRrEOuJIoHf7566oN1uZfMUsBCAAAQhAAAIQgAAEIAABCEDg6gTWnnuvbe/q7UP9IQABCJyVAAJ9ppa1jjgS6MfE+aFjZiuTr5iFAAQgAAEIQAACEIAABCAAAQhcncDac++17V29fag/BCAAgbMSQKDP1LLqiN3nkPDu9k85LluZXMUsBCAAAQhAAAIQgAAEIAABCEDg8gTWnnuvbe/yDQQACEAAAiclgECfqWGtI2YFfSbCmIUABCAAAQhAAAIQgAAEIAABCKxHwObxK5lc295KbmEGAhCAAAQKI4BAn6lBrCOOBHq3f+6KerOVyVfMQgACEIAABCAAAQhAAAIQgAAErk5g7bn32vau3j7UHwIQgMBZCSDQZ2pZ64gjgX5MnB86ZrYy+YpZCEAAAhCAAAQgAAEIQAACEIDA1QmsPfde297V24f6QwACEDgrAQT6TC2rjth9Dgnvbv+U47KVyVXMQgACEIAABCAAAQhAAAIQgAAELk9g7bn32vYu30AAgAAEIHBSAgj0mRrWOmJW0GcijFkIQAACEIAABCAAAQhAAAIQgMB6BGwev5LJte2t5BZmIAABCECgMAII9JkaxDriSKB3++euqDdbmXzFLAQgAAEIQAACEIAABCAAAQhA4OoE1p57r23v6u1D/SEAAQiclQACfaaWtY44EujHxPmhY2Yrk6+YhQAEIAABCEAAAhCAAAQgAAEIXJ3A2nPvte1dvX2oPwQgAIGzEkCgz9Sy6ojd55Dw7vZPOS5bmVzFLAQgAAEIQAACEIAABCAAAQhA4PIE1p57r23v8g0EAAhAAAInJYBAn6lhrSNmBX0mwpiFAAQgAAEIQAACEIAABCAAAQisR8Dm8SuZXNveSm5hBgIQgAAECiOAQJ+pQawjjgR6t3/uinqzlclXzEIAAhCAAAQgAAEIQAACEIAABK5OYO2599r2rt4+1B8CEIDAWQkg0GdqWeuII4F+TJwfOma2MvmKWQhAAAIQgAAEIAABCEAAAhCAwNUJrD33Xtve1duH+kMAAhA4KwEE+kwtq47YfQ4J727/lOOylclVzEIAAhCAAAQgAAEIQAACEIAABC5PYO2599r2Lt9AAIAABCBwUgII9Jka1jpiVtBnIoxZCEAAAhCAAAS2IPB6uAUF9+r53qK0fGWcpR75CGEZAhCAAARsHr8SirXtreQWZiAAAQhAoDACCPSZGsQ64kigd/vnrqg3W5l8xSwEIAABCFyYwOvh/5rrHqqvqX0XRnTOqr+r590J74/qNVbB97O6327V7TF61piFMo6dpR5l0MQLCEAAAqclsPbce217pwVPxSAwRCA1L0ntG7qe/RA4CAEE+kwNZR1xJNB3xPl/bvWk9+dn0d7Z4z8IQAACELgYAYmKTiAN/93v1f3xrF5rrGhODXBT+y6Gfml13897/8HHUqOrXj9NoK9XnX8Q8Vf1K4+xs9QjDx2sQgACEICACGi8pe9LP9e2t9QfrofAqgSYqyzCWf58YVH1uHgmAVTfmcCmnq6O2H12RPlQsP+nEVxGBPqOnamFcx4EIAABCJyDgAa993v1eDzsn1/R3Aj2nZXv39Q6Jcan9n1jO/s1r+rhONyf1RrPKtZ0t/wB9wSBvom/chfPT2z/4uuxZuRhCwIQgAAElhDQ/HuJjfDate2FttmGwO4EmKssaoLy5wuLqsfFMwkg0M8ENvV064hDQT7eZgX9VJycBwEIQOCaBDToTSik71fz6pHbrUocns4rJcan9k23uOGZEwXaDT06TlETBPriK0P7F99EOAgBCEDgYARsHr+S32vbW8ktzEBgHQLMVdbhiBUIVFWFQJ8pDKwjjkR5t99W1CcE+s7x5lqzlclXzEIAAhCAQKEERga93uNGSP/4HvGx6qXE+NS+MRu7HUOg/R49Av337LgSAhCAAATOSmDtuffa9s7KnXodlABzlYM2HG6XSACBPlOrWEccCfQmzrv9CYG+cxyBPlPrYBYCEIDAQQh8GvRWElnjVfTv6v16VHf/I6B6f/29eoQ/BCsEKTE+tc+f/65ej3v9+yl6xc79MeNd+BOub8ruvbZGLJrX2dTvFFfdgs/OnxNMKM/VqynTXeq52fv+B5hV7+r1fEQcnt0fWx1jGF17c68wSv2gwGy/1KjR5/tVPR/1O/H9+MS3mWIn9X75OdzulQurON7uj9fAa4f67KbU38VdPba6V8+Xa7Kgza294h+znViPVWI7Ys5XCEAAAhA4JAGbx6/k/dr2VnILMxBYh4DG553xd2ha480DzFXGxt0ap7+f1cPmV8PzhHhcfLsNnJucL/THyvd7NM/wiPvnTRlTT5vrhG3I9lYEEOgzkVZH7D5TorvfxzvoM9HHLAQgAIGTEPg46K2q1LsLbd/9UT1fr+r1ageTvXfWpwaGqX32MKD5gVpn14TmWqQdp64B+ufrJb6GY/16X1DOu66Xfx+/1fMVPCyYXp4Eejeodf32/e7e998+iIiZyT//Q73icA98cyBGGbr35ut3BYJywgoHNqb6lebf/JWBf1d//TsG3Qc3sUA/l9u9une4BQ8u4vpYDM2svxfgXdw8qofj/KrcEwEf16u0v/n1OTbTjNkLAQhAAAJnIaB5/Fr1WdveWn5hBwKrEDjTXKUZu9u42//+lxaI3Kq7Fov4eUI73o3nCUvnYZPmGTZ2nTmm7ozZgzlIahHXKgGCkTkEEOjn0JpxrnXErKCfQY1TIQABCECgQ2DCoDcpBL9f1bv3q6kDr4NJCcmJfRps9jXX5l34vQOdmtiDhN5pyTpKVG7E44Q/tfWBOjn99lkPqCeVpwH5LRLZ5VvnR2gbAbuzr1tX/y3hs3y69ZxSfaPyZ/mV8CHgMDR5iF+PJB97LopFeGDIvypdH9leXH+r6jrtL7/CqvkiUnW2stmAAAQgAIEzErB5/EqVW9veSm5hBgLrEJgyVkqMid1Ci9LmKppTudXuoV6tcaK7lzvjadU9nhMsqtu0eYb51Bu8psfgQ3WrhuqwTnRgZSYBBPqZwKaebh1xJNC7/baiPvGKm85xXnEzFTfnQQACEDgnAQ2aeoOvtroaoHUGjO3hYEsro6MV06lBc2+fBovudTbv6t3596r/1DMenAYlV1rl0bxaZdL1En/d6hW/+vuZeGXKkEA7099efeV8ipn2uZXcvacgujCxgl7XRfybK5LtOMuvtuh2a6zM1LFm39R2GvSvfUDSxmWqvMDT5oFKe/7QXyG011R6ENCLvTn1mHNuWDbbEIAABCBwRgI2j1+pcmvbW8ktzEBgHQKnmauMjDsH6zg+tu0CHji3N5bWeWPzDJ2z5ZyiWxu+5SGAQJ+Ha/Oe1ECMj4R6veLG/2n2z/Hz6NQzNRJmIQABCJROYHBA2DouYbev4bv30D+rp//zzObVJv5VIdFgrjcwTA1QtRpj4L3fgwK6/Pzuev2JZ7ySRVaHBdqZ5aUY+EIGBsDh+yfdq2qeifet92wOPUxoatOc31ld3rOhmg/4pcP2OVZmysZa3EZiqCemf1N/VXCofnPqMedclcsnBCAAAQiclcDac++17Z2VO/U6KIHTzFVSY1e1STNW7E22UmNpXbNgHvZxnjE0/m3KzjKnUL34zEkAgT4TXXXE7tNWzMciPe+gz0QfsxCAAAROQuDjoFcDw+6fYro/Y/QPgL0gH4vqCwR69wNFndXzwWr6UeTtQHL69apb7X9vTOzLa+1217K3+yeV96UQ7h6AhD8UFf45rP6UtF0R3vrU9bUBl2UwPVam+Ibx0J6/jFtqktPaXl5/BduQzXb/53rMOVfl8gkBCEAAAmcloHn8WvVb295afmEHAqsQOM1cJTV2FaFmrNibjKTG0rWdRfOwptjheUY7dl0+ph6og6rO56YEEOgz4baOOBblw++JV9ykxHyzlclXzEIAAhCAQKEEPg16dbyzKlkDrXv16LyCRftDQXZgMNoTrAeunYxt/vX2lwHPZhB6i/z2ZQ8NUGeW16uvKjbNznuSuD5uS/VtBf2BtvGujduS9/ZqoSS7lI3UvtZab2uQW/uKm3YuM257Xv3lyRrtP+6XSuITAhCAAASuQWDtuffa9q7RCtTyMAQ0F2kHfF3Xdbz4ucrYuLsZb/bqmBpDat+CeViXYNWfZ6iM1NyoHYOvO6eInOJrFgII9FmwVoOvuHEdtInwCYG+c7wR8+nUMzUSZiEAAQiUTkCD2t6A0P/6p62S7x4eEi2bd8XHYm1KZE3sSwqo4udX1etL+nPW9aq3BvMpAdwXMzxAnVVeor51LYbtd2uZGLgnbOqVPZ0BszP0bq6PfpSqvwpfpU71y70Kv/4LhG6Z7+r1qH9Ed+hHYrvnN+XG7ax2if3Wu+Gj/Wlfvqn/Zw5z2n/OuSqZTwhAAAIQOCeBtefea9s7J3VqdVgCGrN3JyN1dXTsdqu6h8ucqwyPuxPjfF/D1Hh8hbr1gqFf/npj6lQdeg6wYyMCCPSZQFtHHK6Yj7cTAr2J98G5ZiuTr5iFAAQgAIFCCWhg695z3nuXvBNe3fvP+3/caIO2x7N6vV7V8xm+8iZabZEQktMD1GZweLtV98ezer5e1cu/474WepOCbgfr1Os1UOy+tkd16g7wWwH6dnfv2b9XdzthanljK2bkS8DMt4krp2brGOg1N1a0q3eKqwnXt+pmbSqh/Fb1GCZtOOMJvzqsgy+KIddunpFi4V7d7y6Ggrr5y+Zz0ziltn+3B0e9+qxW/7Z+iotF7R/49V1st/6wBQEIQAACxyagPm2tWqxtby2/sAOBVQhonGnj2vB3rw42Vxkcdzdj485A39FLj8c1NtVcYdY8bOo8Ixi7bjanWCVgMDJGAIF+jM6CY+qI3WdKdPf7eAf9AsJcCgEIQOACBDTojd8lrx8m7WvzDZR39bQV0s3g+OVWTScE2dRgNLXPW65XXnfeq3h/VM/Oq3TG2uXz9YOrmY1FQlD2QrOrWyxyfy7PeztS32dPxF7BpnuQELSpE7aTDGf5NcLdrdAPGbmHC2893Ih5Ojvz6/juPASK/6w39K2OzWX1D+1Fdes8sJpYD29uzrlh+WxDAAIQgMCZCGgev1ad1ra3ll/YgcAqBGx8Xo/DFe9eNH6+qveR5iqD4+55Ar0X7r+eh80Zj64xpk4/ZFglNjAymwAC/Wxk0y5QYhoU54MV8p/OMVvTiuYsCEAAAhCAAAQgkJ/A4EQmf9GUAAEIQAACEMhBYO2599r2ctQZmxCAAAQgsD8BBPpMbWAdcSTEu/1jgnzquNnK5CtmIQABCEAAAhCAwGwCCPSzkXEBBCAAAQiUTWDtuffa9sqmh3cQgAAEIPAtAQT6b8l9uM464kigHxPnh46ZrQ9lchgCEIAABCAAAQhsRgCBfjPUFAQBCEAAAtsQWHvuvba9bShQCgQgAAEIbE0AgT4TcXXE7nNIeHf7pxyXrUyuYhYCEIAABCAAAQjMJ4BAP58ZV0AAAhCAQNEE1p57r22vaHg4BwEIQAACXxNAoP8a3fiF1hGzgn4cFEchAAEIQAACEIAABCAAAQhAAAIFELB5/Eq+rG1vJbcwAwEIQAAChRFAoM/UINYRRwK92z93Rb3ZyuQrZiEAAQhAAAIQgAAEIAABCEAAAlcnsPbce217V28f6g8BCEDgrAQQ6DO1rHXEkUA/Js4PHTNbmXzFLAQgAAEIQAACEIAABCAAAQhA4OoE1p57r23v6u1D/SEAAQiclQACfaaWVUfsPoeEd7d/ynHZyuQqZiEAAQhAAAIQgAAEIAABCEAAApcnsPbce217l28gAEAAAhA4KQEE+kwNax0xK+gzEcYsBCAAAQhAAAIQgAAEIAABCEBgPQI2j1/J5Nr2VnILMxCAAAQgUBgBBPpMDWIdcSTQu/1zV9SbrUy+YhYCEIAABCAAAQhAAAIQgAAEIHB1AmvPvde2d/X2of4QgAAEzkoAgT5Ty1pHHAn0Y+L80DGzlclXzEIAAhCAAAQgAAEIQAACEIAABK5OYO2599r2rt4+1B8CEIDAWQkg0GdqWXXE7nNIeHf7pxyXrUyuYhYCEIAABCAAAQhAAAIQgAAEIHB5AmvPvde2d/kGAgAEIACBkxJAoM/UsNYRs4I+E2HMQgACEIAABCAAAQhAAAIQgAAE1iNg8/iVTK5tbyW3MAMBCEAAAoURQKDP1CDWEUcCvds/d0W92crkK2YhAAEIQAACEIAABCAAAQhAAAJXJ7D23Htte1dvH+oPAQhA4KwEEOgztax1xJFAPybODx0zW5l8xSwEIAABCEAAAhCAAAQgAAEIQODqBNaee69t7+rtQ/0hAAEInJUAAn2mllVH7D6HhHe3f8px2crkKmYhAAEIQAACEIAABCAAAQhAAAKXJ7D23Htte5dvIABAAAIQOCkBBPpMDWsdMSvoMxHGLAQgAAEIQAACEIAABCAAAQhAYD0CNo9fyeTa9lZyCzMQgAAEIFAYAQT6TA1iHXEk0Lv9c1fUm61MvmIWAhCAAAQgAAEIQAACEIAABCBwdQJrz73Xtnf19qH+EIAABM5KAIE+U8taRxwJ9GPi/NAxs5XJV8xCAAIQgAAEIAABCEAAAhCAAASuTmDtuffa9q7ePtQfAhCAwFkJINBnall1xO5zSHh//Vm/g17n3n/cqlck6OuYt5PJV8xCAAIQgAAEIAABCEAAAhCAAASuTkDz77U4rG1vLb+wAwEIQAACZRFAoM/UHtYRR4K7xPrXz1qcv/+8Va9ft8qJ9U6gf/7TF/TNViZfMQsBCEAAAhCAAAQgAAEIQAACELg6gbXn3mvbu3r7UH8IQAACZyWAQJ+pZa0jjgR6t9+J9M8ft+r241a9B45LyHefssUnLIgBYoAYIAaIAWKAGCAGiAFigBggBogBYoAYIAaIAWKAGDhRDGTSpy9vVjdJKLSH216gv92q56/+ivnwPAT6E91sN+qi+4JPYoEYIAaIAWKAGCAGiAFigBggBogBYoAYIAaIAWKAGLhVrKDP9CghDK5YcPff/7lVD7eK3om2P27V48/+avpYnM/kKmYPQKATT//7f1XV/HP7te0++Q4P4oH7QzFAPiAfKBboH+gfyQf1mPsAQz5c3ICAux/CeyLcJl+SL3PEg7e5QWxTxPYEXNvSvttzp0QInJEAAn2mVrVEHb3CJhbr378Cod6tqOcd9Jla5NhmLZ4Q5v0DCT8I4kGFPZyBB0IsQiwPZhQD5APygWIBobEVGm0cdezhIN6vREDxQL4kX26RLxVvK4UvZgojQPsW1iC4A4EDE0Cgz9R4lqgjgd4PBKN9TrR3Qv3YNf66TL5itnwCig0fBwjTCNM8qOFBDX8x01n9iBDZCpESG+gvEJ4UC9wf9f3BWLr88e5WHmpcrXuEfEm+VCzkypfkn63u7u3LsXyyfdGUCAEInIwAAn2mBrVEnRDj41X0+v5wfx71s/9OerOVyVfMlk/AYgBhFmEWYRZhlldb2UO6XBPp3BN17PMXD4oB179r233yPQ8PG0eVP+TDww0IKB643/Lcb8pp8K35Kt42CG2K2IEA7bsDdIqEwEkJINBnalglaj8wiUX6f27V/Xar7j/rVfOv4DU3j+hHYzt2MvmK2fIJdOKAFfQmZvj7Cx7w4MGVjwHuB4QGiSIIvQjd5IN+PvBMyh/y4eEGBFwshPdIuE3+JH/miAdvc4PYpojtCbi2pX23506JEDgjAQT6TK1qiToW55vvr5+1SK/z3A/FPiNxXivrdU4mVzF7AAIWAwiRCJGssOxMqplIM5F2+RFhmhXpigHigftBsRD2DzaOOsCYDxfzE1A8kC/IF6l8oX1rxYfiLX9kU8IeBGjfPahTJgTOSQCBPlO7WqKOBHrf0Uf7JMS7z9Rxs5XJV8yWT0Ax4OODFeMmxsGDiZUmUaEQo33EB/GhWCA+eJBDPiAf+Bgof8iHhxsQcLEQ5oRwm/6C/iJHPHibG8Q2RWxPwLUt7bs9d0qEwBkJINBnalVL1CNifCjMj22brUy+YrZ8AhYDrKBnBT0r6DuTaibSTKT9pIgHlzy4pH+kfxzpH20cVf6QDw83IKB4oP/gwd0WD/IVbxuENkXsQID23QE6RULgpAQQ6DM1rBK1H/iNiPRTjstWJlcxewACigEfLwhRCFEIUQhRI0KUJpvkC4QHxQIPsniQRT5gheMBhrubuahxtXIk9wf9pWIhV3/pY2yzCKegLQlYPtmyUMqCAAROSQCBPlOzWqIeEefHVs2Hx8xWJl8xWz4BiwGEWYRZhFlW0PPOdXtIl2sinXuijn3ema8YcP27tt0n3/PwsHFU+UM+PNyAgOKB+y3P/aacBt+ar+Jtg9CmiB0I0L47QKdICJyUAAJ9poa1RB0J9H6gEu2Lxfjwu9s2W5l8xWz5BBQDPn5YQW9iBjyYWGkSiLCFsEc+IB+QD3jwoRhI5QO/r/whHx5uQMDFQhgj4TbjCcYTOeLB29wgtiliewKubWnf7blTIgTOSACBPlOrWqIeEeNjIX7ou9nK5CtmyydgMcAKelbQs8KyM6lmIs1E2k+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7s6qFezvGk4m2D0KaIHQjQvjtAp0gInJQAAn2mhlWi9gO/EZF+ynHZyuQqZg9AQDHg4wUhCiEKIQohakSI0mSTfIHwoFjIKTyoDOKNeFMslBpvPkYPMObDxfwEXCyEOSvcLjV+S7+/8G/8L5jIP/nv671KsHyylwOUCwEInIYAAn2mprREPSLOD62Yj/ebrUy+YrZ8ArDMTZMAACAASURBVBYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaOKn/Ih4cbEFA8XPV+uHo+2Lr+ircNQpsidiBA++4AnSIhcFICCPSZGtYSdSTQ+4FgtC8U5FPHzVYmXzFbPgHFgI8PVtCbGAcPhElNstwn8UA8EA8I0YoB8gH5QLGg/sHHRPlDPjzcgICLhTBHhNuKlzh++E7/ohj4Jl78NRvENkVsT8C1Le27PXdKhMAZCSDQZ2pVS9QjYnwozI9tm61MvmK2fAIWA6ygZwU9QnRnUs1EmgcTflLEg0seXNI/0j+O9I82jip/yIeHGxBQPNB/8CBPonvO8aTibYPQpogdCNC+O0CnSAiclAACfaaGVaL2A78RkX7KcdnK5CpmD0BAMeDjBSEKIQohCiFqRIjSZJN8gfCgWMgpPKgM4o14UyyUGm8+Rg8w5sPF/ARcLIQ5K9wuNX5Lv7/wb/wvDMg/+e/rvUqwfLKXA5QLAQichgACfaamtEQ9Is6PrZoPj5mtTL5itnwCFgMIswizCLOdSTUTaVbQu/yIMDAuDMAHPoqBq94vNo4qf8iHhxsQUDxc9X64ej7Yuv6Ktw1CmyJ2IED77gCdIiFwUgII9Jka1hJ1JND7gWC0Lxbjw+9u22xl8hWz5RNQDPj4YQW9iXHwQJjUJMt9Eg/EA/GAEK0YIB+QDxQL6h98TJQ/5MPDDQi4WAhzRLiteInjh+/0L4qBb+LFX7NBbFPE9gRc29K+23OnRAickQACfaZWtUQ9IsbHQvzQd7OVyVfMlk/AYoAV9KygR4juTKqZSPNgwk+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7kSXTPOZ5UvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfuA3ItJPOS5bmVzF7AEIKAZ8vCBEIUQhRCFEjQhRmmySLxAeFAs5hQeVQbwRb4qFUuPNx+gBxny4mJ+Ai4UwZ4XbpcZv6fcX/o3/hQH5J/99vVcJlk/2coByIQCB0xBAoM/UlJaoR8T5oRXz8X6zlclXzJZPwGIAYRZhFmG2M6lmIs0KepcfEQbGhQH4wEcxcNX7xcZR5Q/58HADAoqHq94PV88HW9df8bZBaFPEDgRo3x2gUyQETkoAgT5Tw1qijgR6PxCM9oWCfOq42crkK2bLJ6AY8PHBCnoT4+CBMKlJlvskHogH4gEhWjFAPiAfKBbUP/iYKH/Ih4cbEHCxEOaIcFvxEscP3+lfFAPfxIu/ZoPYpojtCbi2pX23506JEDgjAQT6TK1qiXpEjA+F+bFts5XJV8yWT8BigBX0rKBHiO5MqplI82DCT4p4cMmDS/pH+seR/tHGUeUP+fBwAwKKB/oPHuRJdM85nlS8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStR+4Dci0k85LluZXMXsAQgoBny8IEQhRCFEIUSNCFGabJIvEB4UCzmFB5VBvBFvioVS483H6AHGfLiYn4CLhTBnhdulxm/p9xf+jf+FAfkn/329VwmWT/ZygHIhAIHTEECgz9SUlqhHxPmxVfPhMbOVyVfMlk/AYgBhFmEWYbYzqWYizQp6lx8RBsaFAfjARzFw1fvFxlHlD/nwcAMCioer3g9Xzwdb11/xtkFoU8QOBGjfHaBTJAROSgCBPlPDWqKOBHo/EPy/W/X681bdm9Ub/twft+rxq1nNkbjGX5fJV8yWT0Dx5OOAFfQmxsEDYVKTLPdJPBAPxANCtGKAfEA+UCyof/AxUf6QDw83IOBiIcwR4bbiJY4fvtO/KAa+iRd/zQaxTRHbE3BtS/tuz50SIXBGAgj0mVrVEnUktruV8c8fdRK/OVH+Z/1PYv39560KV8+7bbOVyVfMlk/AYoAV9KygR4juTKqZSPNgwk+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7kSXTPOZ5UvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfuAXiPTvPxvBvRHiw+OP5unr859WpO/YyeQrZssn0IkDhCiEKIQohKgRIUqTTd+/kC/IF+QL8gX5gsUu5Q91N/VQ42r6y3pVPOOF/A8qPONNo5zCtiJg+WSrAikHAhA4LQEE+kxNa4k6EOfD1fOvaL87JvH+/mcr0LOCPlMDHcysxRNCC0ILQgsr6HnnuonuOVe8Idwg3BBf5/kLHRtHHWz8h7t5CCge3KdyPff7ee53tWkp7at4yxPNWN2bAO27dwtQPgTOQwCBPlNbWqKOhHi//8etekf7nRBfNe+gv0WvuTFbmXzFbPkEFAPuU4NOJhJMJIgH7gfyAe/EVQyQD8gHigXGB+nxgb9Hyh/y4eEGBFwshDkz3Ob+Sd8/5Jdl4w3yzwY39k5FWD7ZqXyKhQAEzkMAgT5TW1qijoR4/xobBPpM1M9r1uKJFfSsoGcFfWdSzUSaibSf9PIqH3t4Cw+EeoS0vpBm46jzDhWp2QwCigfyJflyi3ypeJsRopx6IAK074EaC1chUDgBBPpMDaRE7Qd+gUivH4jVK27C46lX3HTsZPIVs+UT6MQBQhRCFA9qeFDDgxoe1PAXVdYX8KCOB3V+PP1hfOTPKX/Ih4cbENC4WuLslPjRueQb8s038UL+2eDG3qkIyyc7lU+xEIDAeQgg0GdqS0vUgTjvXmPz+ln/SWX8nvnqn1uV+pFY3kGfqYEOZtbiCWEWYRZhFmEWYRZh9oMQiZDUX0EtJl4kgZ/dQ1fhYeOog43/cDcPAcXDVeKf/Ff3CXu1t+ItTzRjdW8CtO/eLUD5EDgPAQT6TG1piToS6N1+CfG3H7fq8bP+p/Pdp38ffXCdjmVyFbMHIKAY8PGBsHA5YYGJ1b4TK/jD38UA+ZdXISgXEA/HvB/8PXyAMR8u5iegcbXuafI7+V2xkCu/k3/y39d7lWD5ZC8HKBcCEDgNAQT6TE1piToQ2kPh/fnzVt2bHyhy595/3Krnr744zwr6TA10MLMWT6ygZwU9QiFCKSvo7SFdrol07ok69lnhrhhw/bu23Sff8/CwcdTBxn+4m4eA4oH7Lc/9ppwG35qv4i1PNGN1bwK0794tQPkQOA8BBPpMbalE7QcmAyK9xPdQuI+3O3Yy+YrZ8gl04oAV9CZm+PsLHvDgwZWPAe4HhAaJIgi9CN3kg34+8EzKH/Lh4QYEXCyE90i4Tf4kf+aIB29zg9imiO0JuLalfbfnTokQOCMBBPpMrWqJekScj8X4oe9mK5OvmC2fgMUAQiRCJCssO5NqJtJMpP2kiAd1PKijf6R/HOkfbRxV/pAPDzcgoHig/+g/yOJB7/p/4aV42yC0KWIHArTvDtApEgInJYBAn6lhLVFHAr0fCEb7QmE+ddxsZfIVs+UTUAz4+ECIQohCiEKIGhGiNLkmXyA8KBZ4kMWDLPIBKxzLH+1u56HG1cqR3B/0l4qFXP2lj7HtQpySNiRg+WTDMikKAhA4JwEE+kztaol6RIwPhfmxbbOVyVfMlk/AYgBhFmEWYZYV9Lyz2h7S5ZpI556oY3/9FYpi6vpLbbtPvsNDceBjofwhHx5uQEDjavID+WGL/kLxtkFoU8QOBGjfHaBTJAROSgCBPlPDKlH7gd+ISD/luGxlchWzByCgGPDxwgp6E1/gwcRqi4mVyiDeiDfFgvskHogH4uFYD1r8PXuAMR8u5ifgYiHM4eE2+Z3+LUc8eJv5Q5sSdiDg2pb23QE8RULghAQQ6DM1qiXqEXF+bNV8eMxsZfIVs+UTsBhgBT0r6BEGO5NqJtJMpP2kiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+BB6xYPWhVvG4Q2RexAgPbdATpFQuCkBBDoMzWsJepIoPcDwWhfLMaH39222crkK2bLJ6AY8PGDEIUQhRCFEDUiRGmySb5AeFAs8CCLB1nkA1Y4lj/a3c5DjauVI7k/6C8VC7n6Sx9j24U4JW1IwPLJhmVSFAQgcE4CCPSZ2tUS9YgYHwvxQ9/NViZfMVs+AYsBhFmEWYRZVtDzjm17SJdrIp17oo79Y70ahfY6fnvZOKr8IR8ebkBA8eA+ub+Pf3+rDUttT8XbBqFNETsQoH13gE6REDgpAQT6TA2rRO0HCiMi/ZTjspXJVcwegIBiwMcLK+htMgUPJpaalLlP4oF4IB4QWhQD5APygWJB/YOPiQOM+XAxPwEXC2GOCLcVL3H88J3+RTHwTbz4a/KHNiXsQMC1Le27A3iKhMAJCSDQZ2pUS9Qj4vzQivl4v9nK5CtmyydgMcAKelbQI0R3JtVMpHkw4SdFPLjkwSX9I/3jSP9o46jyh3x4uAEBxQP9Bw/yJLrnHE8q3jYIbYrYgQDtuwN0ioTASQkg0GdqWEvUkUDvB4LRvlCQTx03W5l8xWz5BBQDPj4QohCiEKIQokaEKE02yRcID4qFnMKDyiDeiDfFQqnx5mO0/CEfHm5AwMVCmLPC7VLjt/T7C//G/8KA/LPBjb1TEZZPdiqfYiEAgfMQQKDP1JaWqEfE+FCYH9s2W5l8xWz5BCwGEGYRZhFmO5NqJtKsoHf5EWFgXBiAD3wUA1e9X2wcVf6QDw83IKB4uOr9cPV8sHX9FW8bhDZF7ECA9t0BOkVC4KQEEOgzNawStR/4jYj0U47LViZXMXsAAooBHy+soDcxDh4Ik5pkuU/igXggHhCiFQPkA/KBYkH9g4+JA4z5cDE/ARcLYY4ItxUvcfzwnf5FMfBNvPhr8oc2JexAwLUt7bsDeIqEwAkJINBnalRL1CPi/Niq+fCY2crkK2bLJ2AxwAp6VtAjRHcm1UykeTDhJ0U8uOTBJf0j/eNI/2jjqPKHfHi4AQHFA/0HD/IkuuccTyreNghtitiBAO27A3SKhMBJCSDQZ2pYS9SRQO8HguG+X/UT1/uft8qJ8r3jzT6/P5OvmC2fgOLJxwFCFEIUQhRC1IgQpckm+QLhQbGQU3hQGcQb8aZYKDXefIyWP+TDww0IuFgIc1a4XWr8ln5/4d/4XxiQfza4sXcqwvLJTuVTLAQgcB4CCPSZ2tISdSjGp7YjgT5cOa9ts5XJV8yWT8BiAGEWYRZhtjOpZiLNCnqXHxEGxoUB+MBHMXDV+8XGUeUP+fBwAwKKh6veD1fPB1vXX/G2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuBX0qYb/bpPK2glyivTx33djL5itnyCXTigBX0Jsb5+wIe8ODBFQ+ueHDFgyse1Fhf4MQn+sf+gzvG0uWPd7fyUOPqrYVayqsfll4xP5F/trq7ty/H8sn2RVMiBCBwMgII9Jka1BL1iDjvRXhW0GdqgXOZtXhCiESIRHhBeEKIRIjkwaTFgBc94AGPD+MjG0eda3hIbb4koHggf/QfZOkhAg/61nvQqXj7Mly5rHACtG/hDYR7EDgQAQT6TI1liToS6P1AMNwXCfS947yDPlMLHcus4snHB0IEQsQHIUKTK+KFiadigYn2ehNtMeX+4v5SLHB/HeP+8vdsacO/16O63e7V812aY+f2x8VCmMPDbe7nY9zPR8u/Reafc9/mm9XO8slmJVIQBCBwVgII9Jla1hJ1KMantiOBXq+2CT/NViZfMVs+AYsBhFkvzjseRxuY4y/vgFYMEL/cv4oF90k8EA/EQ/7+wcZRQ0M+L5TXoq0/9/6sNtHMEeiHWiTrfsUD+Zf8u0X+VbxlDWqM70aA9t0NPQVD4HQEEOgzNakStR/4pYT5Zp/O4x30mRriJGYVJz6eWEFv4jw8mFhtMbFSGcQb8aZYcJ/EA/FAPOQX1sV4jfvN20iMC9/Pu7+fH6/2oN8X7mgPrbuFQL8uz4nWXCyEMRVuk9/p33LEg7c5MT457VgEXNvSvsdqM7yFQKkEEOgztYwl6hFxnnfQZ4J/QrMWT6ygZwU9wmBnUs1Emom0nxTx4JIHl/SP9I8j/aONo3pjxFf1cOLKVivm4/IR6GMiC7837fnh4Yrigf6DB616CJhzPKl4WxjcXF4oAdq30IbBLQgckAACfaZGs0QdCfR+IBjui15x0zvOO+gztdCxzCqefHwgRCFEIUQhRI0IUZpski8QHhQLOYUHlUG8EW+KhVLjzcdob/g3TdDtXbbWDgT6tUg2dqa1p4uFMGeF26XGb+n3F/6N/0VROv+sHP6Y24WA5ZNdSqdQCEDgTAQQ6DO1piXqUIxPbUcCffjueW2brUy+YrZ8AhYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaO6g353tXzXou1HxZdV1XVnit7t9ujCt6M463Xr8xJ/PCrF+NvVaecQKB/PWo/ZLtznvxubOgc99k/L/Yz9vHTcVdYI3Q3QnaqnLqeznZkTw69n9V95Pq6Sp/LqXyd6zp0GXUZ61VFIZuhH+ANz9G94T7dfr6TLxUDa8WD4k23MZ/nIkD7nqs9qQ0E9iSAQJ+JvhK179hTwnyzT+fxDvpMDXESs4oTH0+soLfJEzyYSGoSxcQaYYF8QD4gHyCsKQZS+cDvS40LO0JyLGbrgkZIjl6FUwvGKaG4u89bGRToa2H+/mx/llZCtLRud70XoCeU768Nz3P1C75/Ol6JR1h443voYyiI26k67+7e69+yTHGaWk4t0MeM9FCgLaNuKVbQMx4qczw0mH+UYvg8LAHXtrTvYZsPxyFQFAEE+kzNYYl6RJznHfSZ4J/QrMUTK+hZQc8KL1a4scLPHtIhRJQpREgkpX1oHy9aFLCwwMZRg2NECb7NKvZA0HaX1AJzLAb7I7132NfC9TyBPhS+axfTDwR67jdienv9J4H60/HhusbCvgR6E+e9c+IYser5Ob0cCfTdcnyj+PFAd//n+jk3FQ+lxKdyJv6c80Gz4q13/7LjFARo31M0I5WAQBEEEOgzNYMl6kig9wOvcF/0ipvecd5Bn6mFjmVW8eTjo4CJLhOJepUi7XHOiRTxTXwjLCMsk9/Pl999m34c/klgDn84dlz0jcX7+QJ9QswffSgQVGJQ+L5Vt65ybRfV/g4dH65rXa9WeE/Xs+EXPeDQK3OmPEiIy6kF+gSjRN1VzlDdBcHFQniPh9vkf/J/jnjwNhWAfJ6KgGtb2vdUTUplILAbAQT6TOgtUYdifGo7Euj13vnw02xl8hWz5ROwGGAFPSvoWUHfmVQzkWYi7SdFPLi0vyqAx/mEZT00JN99n+9sHDVxyCcRu9a4h0VrZ25Lgb4Wr5tV/sH73Vvhu65g97xWVFf1h483dQ1si1392dqqbcTC+UyBfkI5OQV68iX5cov8qntI9x+f5yJA+56rPakNBPYkgECfib4StR/4pYT5Zp/O4x30mRriJGYVJz6eEKIQonhQw4MaHtTwoIZXHVlfgHD9vXAtceoK4wtfx6njws774ssQ6OsHAZEgnlxFHlSyOR6+Dz446l5s3/yQq4T38bqG164i0A+s8g/LySnQXyn+VVfy5T75clb+6dwAfCmdgGtb2rf0VsI/CByDAAJ9pnayRD0izoer5Me2zVYmXzFbPgGLAYRZhFmEWYRZhFmEWR7UWgz4STE84PFhfGTjqIlDvlh8jlfJt2YSgnZH3G/P1Kr1jiatH1UNfiC2viK2G39v7H4S6PXjsrdI2G/dqn981o4PrYAPLrCi3Q/BxnaHrq/9b1f6D53XLyenQE/+YAX9Fg8u5uafxF2w7a7BvLStG0cp7XDtexSw+AmBCxJAoM/U6JaoI4HeDwSjfaE4nzputjL5itnyCSgGfHwgRCBEfBAiNNkgXph4KhZYMbfPijn4179nQPwRfyX0R96HeMjnhSitHm8ONuJU5z3mWmneUdcbkfkWXV81YnrwHnaJ886HjgmVdbtVrXit1+aE4neqrKac8FrvZ+hPdN2n4w5Bsq5u973zXvv4IUZNb0h4jwX66eXME+iHyu82vGuHMCbDbfIV+SpHPHib3TBMf3u/qsfdPfxqXmV1v1eP1zt9bq69CPSzyKqtZl3EyRCAAAQSBBDoE1DW2GWJekSMD4X5sW2ztYZja9nwHXc4cVjLMHZSBCwGEGa9OO94IHwhfCkGiAfuB8UCwgrCCvmAfJDKBzaOSg2yApFc54VieXtJK4jrvFsgwrfnBeKzRDanyjfCd1+gd4K6hHS9Xz41xk6dU+8L/Q0fBtR+hoJ9I7TLL//ZPV7XI1HXjuOyE/s5JJAnBHpf0Ody5gn0MfvYv7p21n6MJxlPb7DwSfHWyRGpL69H88qpW3V/PKrHI/je+yublIGV9iHQzwI5uX1nWeVkCEDgigQQ6DO1uhK1+/wkvn86LltJV+NJxdBEIXnxgp0I9Avgzb9UMeDjaYOBpCa3lIfQoVhA+ET4JB+QD8gHPBhVDBwxH3if5w/BuOKEBFwshDEcbjPeYbyTIx68zQ/3UvJ3Jvwzp3vnL2w+mFl+GIF+FkPXtlPad5ZRToYABC5JAIE+U7Nbos64gl4rZMIFLfGfn2aqnvvb28R7J7OVdnnDFk+soGcFPe+g70yqmUgzkfaTIh5c2ipIePAgRSI6+bHNjzaOuvyIEgCOgOKBfEm+3CJfKt7G7z79hUzqL1rGr1z9KAL9LKTT2neWSU6GAAQuSgCBPlPDW6KOBHo/EIz2hSvoU8fNVsfX5k9Ct1ox3ym7QqCPeSz+3rRn+LQlsKkY8PGBEIUQxYMaHtTwoIYHNbyawfoChOhWiJbYxHihLzx6JsHYis3rEtC4mvul/qsg8kU/Xyg21upfPucfCfTR71QM3qbv6vVsX4HjY3roffWN4N6fZqrM6KFAINC/3Wt37u2rt+4P90Ku+L931T3PnX+vHsnX8vT9vt+f1atjcso57oJ39Xrc7bVAjsH9/qh6r+wP6u/9tFd8Be/3fz+rR1DPtO8dJ+2LZ+/GZPwHAQhAYCEBMslCgEOXW6IeEeNDYX5s22x1ChsXdDun5vjiO7r0ex1zFHd+m+PtaTGAMIswizCLMIswizDLg1qLAdc/ri2kYO98r/KxcdT5B5TUcAIBxQP5g/y5Rb5XvH0MzUZIduenhXBZkLB+q25OlPfvq2+Fandt579AoO7st9++SAv08tuJ3uH78Ds/oN28gsf7fH9Uz9erer1asTv8fQxXdv0aH1e/Z/Vy57qHDPeupjDlHCfOP72gfu/a8uJ71179l/81q5qtq0/7Q7x3bUf1jH3vsmu/iVO7hy0IQAAC3xFAoP+O28erlKjd5yfx/dNx2eoWqk5pylP29lzZut2ijtg616hDc4WmOvVAoFcnKtvxmMD7HQw4hs+L/Yx9/HTcO1s97Kl4/bQ/9qd+NZCzHdnTic2PeA37Oa2cmltdhy6jLmO9qkjl1Z/dc8JjWwwkVYYrV9vuk+/wIB7OJ1ypTbm/ub8VC+R7+rsz5gNfJz8o5X9XJ+BiIYzxcJv8R/7LEQ/e5oQbr7vCuxGyoyXrNnfU3NXsNgu+bt15ZHIu76/RXDiac9u8PbJTDdh/v6p35GOlczt/7d+U19lnzjcbU87Rj1QndBDN40M2A/Uxju6BSLjaXzZG/Wz9dm07tX3bq9iCAAQg0CeAQN9nssoeS9TZVtB7RT34k66oY7VaNB1p1MHUgnG30607qe4+b6bp1MJ+Th29q2fYoUmIDs/1dieU768Nz3OdY/D90/FKnWlYeON76GPYGdupOu/unqa3LFOcppaTZjQwENIgxhyyBvQbFk+soPcPDPwgiBWk9vAEHgirCKs8OFEMkA/IB4oFhMZWaLRxVHd4xbeLElA8kC/Jl1vkS8Xb9NstfsWLexWLrh6aS9bHNc8N576ak7Y2PtjSvDgUrZtLkvZlrvOZ8lP77tWz9x4aXTzjHP86m3f1fof/XvWragINQfXvMHHFpbQD74Z8aDUBeZf6nN++KSvsgwAEIFBVCPSZosASdSTQ+4FgtC9cQZ86braSvqoDqZ/c3sLOyP6MLNW59IX7usOdJ9D3OjoJzZEfPdebDrG9vvGnP3JoLv10XH8y169rLOxrYNEtShyj63t+Ti9Hg4FuOQN/kSBuvZPr6isGfHwgTCNM86CGBzX8RUtn9SNCZCtESmygv0B4Uixwf9T3h78negNSdlyRgMbVukfIl+RLxUKufPld/nFCvV7Fojlqfw7fuYcbcb3zGppmX3+aOTD/HRHoNb9t5/Aq3b2H/lk9/et2wlfiyO/mvPBd7+71PM/EO+0/ntMwiP5qXve1/wy1iMH6DOkLA1xU1ehT5Ua7+QoBCEBgNgEE+tnIpl1giXpEjA+F+bFtszVatDoS9361Z/PjLUOdTm2oXh3edprzBfqEmD/6UCCowKDwfas6A4rgktrfoePDda3r9ameDT9jp4Jru+0gZHo59QAmwShRd/szwP7IyTtiMYAwizCLMIswy6un7CFdrol07ok69vmLB8WA69+17T75noeHjaM0vOPz0gQUD9xvee435TT41nwVb9/edJoD19PEZi7am7M21vcQ6N0PyQ6K5e0cPKy/E/PDH2VNLNb3gn/6nJbBq7N6PlhJHxaGQB/SYBsCECiYAAJ9psZRR+wHJiMi/ZTjsjXF1WQHPiD6binQa9W66qLPVviua9c9r9+hDx9vOuoJg4PaRiyczxToJ5STQ6D38cIKehMz4MHESpNAhC2EPfIB+YB8wIMPxUAqH/h9UwbTnHN6Ai4WwhgJtxlPMJ7IEQ/e5pd3Vnd+r0V5/XmyM6+5cmeOPShQD9gaPL+138oLsuFewxO+iF77034KhXvnvmMztEDP16l3zjTbKmN41f/Qwrt59r3/7mE7/0EAAhBYSIBMshDg0OWWqEfE+bFV8+ExszVUWLi/6cA6T9jbHjQ8s/kV9bbTTAvXA69k8eXEIndtPhb+6+/RuclV5IF7zfHwffDB0fadcfa++KEOtnOV/5KuZ9MR91Yj1HbbQc70cnII9GMTTx1jYsHEwuUM4gGhSjFAPHA/KBboH+gfrpoPZo2l+0NH/qV0WQAAIABJREFU9pyMgOLhqveD+gTqv834QPE2ehu5ua9/p3p01ruZe9qcV69b7f4OnL/Kzo3m3T2Buy5DYn5vvq3z4x+b1StZO/sb/1Jz6Lt7ENZqDVHNmq9T5tb9c+R7O0cPrPtV9cH3pj79c/t266sQ6AN6bEIAAhsSQKDPBNs64kig9wOhaF8sxoff3bbZmuBrLD7HYnlrItEhNZ1XrOerA+zsn9zRJcpxTnwS6G0FQDTAaCvQrBDQ8SGBPbig2YwZ1buHrq/9bzv0ofP65eQQ6H38sILexGd4bDOxYCJXi/1njLfXH66P+Vf1/Bvh8oztq3sXYZ74Jr6bFdOJ4Rq7rkfA3Q/hPRFunzVfqq8/a/1K7+98jI3darY4zb2utn6H++Oh98/HYnwzv3Zx7N7j7t/7PnSuK1SCc2v77sXze1V/RiK6n+fr2M0/OHBl6DU27by4rpBW+N8fz+r1elXPZ3tuR6D3dbxXOu8VvObGdIYp5/hiWwbO3vP1qpy9Z8Os4+Nk3UINJF4RFx2OPi2fRPv5CgEIQGAuAQT6ucQmnm+JekSMj4X4oe9mKyzbdzRRp9F0Pp0/EVNnb72eMzLU6TQdXfAEXOK886FjQmXdugOG/mr5VFlBh6oXznk/w/pE13067qv1rAcOHUebP8UL9i0T6NuHCx3OeqAQlDNPoG/qG7APm9tigHfQe3He8Sh9II5/rGBXDBQbr3//2yZb8tV9Fusv+Y/8R3xyf37Z/9s4KhxcsX1ZAoqHS/R36uv/+C/548v8oTHSt/GiePt4w71fXmCWEO6uq1fVh6+OkZV38txn5zUzOtdNVF/V8x6I+M1q/eRiPj/PrxfBvTtiu/tR12FfVM/brX7dTd/2u3o97jb29OffH1XX5ynnqF4Tz210i45o7000mkQ4f/f7Ix1CxQ18qt4Dh9kNAQhAYDIBBPrJqOadqETtPoeEd62O/3RctnoeBCK5zul3PO6qVhDXee0PyUZWJeg3K0u8CN3s6/RdvmwnqKsD00p/rWgP7abOqfeF/oYPA2o/Q8G+feed1SH5J3OJunYcl53Yz8bHnkBe2wv9rGv2uZx5An0g/Hv2Xf/aOiNMa5CMkIiQ6u6LS8aDJtuD9f9v9Why+PvDX9zcbr9Xry+E7/d//uUn+vf//LI2uGx7fMGP/EX+4n7ZPn975uHwlO3LEnCxEN6D4XYx+Vl9/aCw3vT1v/27U5fY//ov5W7W18fHx76rry+Sz4fxjauX/pXgv/fhsnfcuSvu2pb2PXcbUzsIbEUAgT4TaUvUuVbQZ/Ibs2USsHhCCGIFKStIRyeiYxPNkiZq8uVbf/3qqj/+O3g/eIH+t39XTqD3k4Z4otpM/B9/DRyPz4++a9LuBPqk/ej8pfXl+rKEBtqD9lAMHOX+t3FUmcO8w3ilxTT9hSuHqYJ3VPFQdPz+XQvvt6avd/dc1996Rfyt6ev7x+vz3XjB9fVDx3UvDx13ZephfLf82B++D/Fx+/2xY90meDuRAO07ERSnQQACHwkg0H9E9N0Jlqgjgd53ztG+cAV96rjZ+s4VrjoBAcWAjw+Er6JWxHya2HAcIUsxsNr9q1V1K6ygl2/uczX/mhyFve1XCNOe5BvFAPdf//7zTE4wJtyzCmcT6Iu+X9TXL1xBT/9exviG/LNn5spbtmtb2jcvY6xD4CoEEOgztbQl6hExPhTmx7bNViZfMVs+AYsBhK+vVwBpEsZEpYyJCu2xTEhcvIKeB3086KM/oT+50IM5G0eVP+SLPGxeqRi9rjE6ia8zCSge3Gex45GVVtAXWz/yz8yo5fRSCSiflOoffkEAAschgECfqa2UqP3ALyHSv3/dqvuP+mmrzn382X9fvY55O5l8xWz5BDpxgLBmkyl/X8ADHlcTGrWqblBYGHsH/a/q9ce/Oj/Qdf/t9+r1d/Tg5q/f/Wog92fx7nzloGfzZ/JVc1x/9q4HX6///B7Z/re997a+X39VQ+d07+f61TnhD6W544+/Eu+8b3xxx99/dct/8I588sPV8gP19THfzSd1fvP7yh/yRR4i0EdAVvnqYiGMkXBb/dnuwrb6+i9X0A/19Z36Bf1n29fXfb6vf3C85ZHun/V7NrI/1NfreG2vHhOoPfznb0H5YT5rfNGr+drxwcD5zbXd8r5/1U/t7/fX+xhbJXoxUhoBxW9pfuEPBCBwPAII9JnazBJ1Spz/sx4UOoH++etWvX7dqkcj1t9HRPpMrmL2AAQsnsKBamEDz6UDV65ftqIaftfi990K+l/V87em//nj39Xrr/96sbzOL/+qnn8HE89gUu6O3//4vXr89q/KCfTueyjQ++//c0J++9BZtu/RRFvn3KPyVbaLY2dPft6a6x/RQ4U43t01Otdtfzo/vp7v17p/aO/rtbfPES53bfZfI6w3QrDPS6+g8Pezfph5f1bvzu57dbvdq+e7qvQ6Gflef9bH2ks+lONOfD2q2+1RueJfjzZPq5zWltt6V897eE59nZ3jbd2q/oL++DpnI7p2ti9W6uobIdNi88HXK+jV19fCtfXHTSzG/W3Loj5ffb3jomN6GO++h/24/+4ezLvxQfCgX+f4481YIx4PVP+rhX5fxm//qh5/1AsDJLzf4wcTGpc04wK3uMBda+cX/Js4vo6b5p/VbxkMjhCgfUfgcAgCEJhFYMuR6izHjn6yJepIoHf7q39u1fuf/mp5/6N+bgVg4hp/3dGh4P/XBBRPPg4Q5lkRyoOawRWSxU601/xTbq2q80L0735Sq4mt+wzFafcjsWKiPNL7sbjAns6VAH+7RcK97DUTZU3abaL94cfqvPA+9uO1//t/lX6ANpXv6n6yKwS0vt7sIYOEBT9x/1Ce6pwqT8dkj+/deIIHPBQDR7h/vI9fj8RmXCjxPVSxG2E7/HFVCfB2WnNdeE5Vjaygn1hOLdDXontrW4J6V0T3An740MCVEX5PCvSNj+F59jAgeqDQXO/a4pMvM4jPPtWVH8ZsuF1MvlffbA+q4/6++Wu43+ofk9W9qD5Ufb3VR/ZC4Vuit3sw3jykt/Ndfx8cr+1L/L/5H6FXmV1+jfD+YTwgP92P4Havb378Nh5/mC/Rink9yPhQnnzt1G/D8bSv4+xI5YIjEHBtS/seoaXwEQLlE0Cgz9RGlqgjsX3sXfPPZhX9K7rGbGXyFbPlE7AY2HAgufdAlvIRfhQDftArYXhNofvA95NWjCk3JD87wnQzqW5WnL3//lXpn7v24VbWh+cHAnySf++4Ju3RxLnTXjrnVj1Tr6rx7aEVdb9Hr8ap7wdN6NsHA+kVfnXstOXFf3qv2HKfyfoRb50HO/AiHysGjnq/OL+97xsM+epV6l3h2xXbE79ttbo7txHMI5F7TKCfXE5SVNfK+nA1/MjDAHFL2Bryw3wP65S43pse2q9yV/5UPBQdzxKem9gNfe5sR8J0/SDcvbqu7k/V17//boTv6HxnS31qikd8vP4LN/cXdbV95Ya2P1XfO208kOqf1dd3/AnGHSqzPq7y6hX1Otb6s3/+dn56X1eOY8yVQYD2LaMd8AICZyCAQJ+pFZWofWccCe4S6d176N3xx8/6nwSXUKDv2MnkK2bLJ9CJA4QjhKMDC8slTpzkk8/XR7i/tArO/UVW0t/UO+i1Iq3ud8KcEm7bivvBiXAz0R047oV+NxFtVvyZPQnhf/+7fhjQTFYf//mvrcKr+Te+RysCbaLdlNtZcad9CR61kFCL/YdpX+5vH9e019D9Xd+D8JnPxzPLPuQbFrnrFfORcK9V8D4nRqvNva9D9ob269U4QTle/E7YTqzYr8X2W3WzZf0RsJ6QPuyHu7In3s/wJSp51a8uFsJ7KNy2/ibZv254/6mv760w14PlVH/Z9v+qY+8z7F9H+k8/vkgdDx8cuFfT/CdeAV/792k84P8iLlwYEPH2fv/x37Y/aHxxDxO67TX+YL+U9vQ+rxrFGCuFgO6xUvzBDwhA4LgEEOgztZ0l6pQ4734gthkY6rzwMxTonZivY5lcxewBCFgMINy0A/VoIO8nEvCBj4Tgk8eH70PCiWtU3/7EtzuRb1fUBSvswvtncCLcCAMfjtvE/JZeQff+qyvUt39an17hZ/e3xIKm7pp4uxzZXwGoVXU3W42v883eReKF+u6/glJt4GJV2+6T79vwsHFU9jFfI1gPjvMD4bzxZVwUHxLAZ5QzUxTXq3dqZpG/JxPoi77/JIRH/V2bP9L9pfr//gr6pr+PxguOQb//bB9EDB13/XgdI26uGr16LhhPpMcD7YOE3oN8d636+jBfBuMOMajbT309K+izpzcKSBLQfZA8yE4IQAACMwgg0M+ANedUS9SRQO/261U2j1/d99BrPwL9HNLXOFfx5D41KGVij7BBPFz0ftCqusF8kJr4zlxhNjgRboTOT8cb4dHnrpEHCW9Nwm2F4PhEW3/23llBJxsJHqygR5hWn0m+vGi+DIRCHwPZh41DgvpAwY3gfb+7H4cNXzej84fsDe3XdcHnTIHerrTV/YFIfzKBvuj8oL7e+sc4n3cfvNd1UR868cH0SP/p7X067n43RucMPkiox+vxeOBT/+zO7zw4aMrp9P/+/p45vtnpweg2+cfuXjY2JOBj241B+Q8CEIDAQgJkkoUAhy63RB0J9G5FvF/Z8KP/Y7AP3kE/hPPy+y2egommJhXu0w/6mmN8hwfxcH4hav4K+vEfX638O+nbFXNavdafCDf31+BEObz/2gcFw/mqWQEYTexdDHcm5i6//d3aa1fc1+Ulz//fTKGC/Mpf4NCfnnY84XKE7xuzjyiH3iWfKrgR2f072tM/2mrvce+9cmZGOd8K9JVelxO8Hqcn0CdeY2NVTTxEWOCLmV1hQ/HgY6LU8fOXK+iTD7KD/u0d/RisY9Drb4PzPx2v/tf0zYMPEtzYou2/NR54/VHfkyrb5i/W10d/gReMO2Sjbj/19aygX+HWwMQXBFwc+lj84lougQAEIBASQKAPaay4rUTtk3Uk0r9+NgOS5vP5Z/eVN+EK+o6dFf3D1LEIdOKg1IkEwsZphY3uRChewcX3zfloVV1ixXjtSzsRjv903D8gdpPxP+o/TX/99e/q+Uc9Cfb9lfLL4ES4ae/4eCMkOLuvv/5bObvKW4+/6mvc9/vtX75sd477rj99d+e05bf+u3fZP/74vXoEPmoyb+c3vtj3QFj4tEJPbec+U9dznPtbMUB8HP/Bp2/DLYZ/Wnkeier+1THBvvrVNoH4nbxuRIhPnt+I6kE51VRR3NsLVsvrh2tvwb6EQF8l/Rh44DDVl8zt5GIhvKfD7WL6A/X1g8J301eG75T3/V/z4Lvp659Nf6u+3vWhVt+R/tPnvvi496keM6ivD/txf83E8UAo2jt/hvp6a49g3GH++/qygj7z7YL5DwRcPPqY/HAehyEAAQh8IoBA/4nQl8ctUUfivH4g9tmI8zrPve5Gwn0o0PMO+i8b4GSXKU78wBchqZ1YBEKc2NhAvjnGd4RHP2g+WTx8s4K+vkfqiWz8OyjPv37Z67M8r8GJcBNPveO/qtcf/+r+vspvv1fObsu/Pkf5zH/+NrTi7Zd/cBD6ee/Za4V/Z6sn3LOCnhXx9JfB/dfeL1fsL5V3thseNqvHG+HGl98TzW/V/fnuuKT3v4enmgDubQWCvr/yQznunBmiuMoXr1sozputkVfxhPX1fxnQqd4sX6IrV/3a1q/gB09frqBXX+/65LCet4H+1p3T7z/bfBEfH+rr2/H2lPFAa989OEj19a29+tzwL/uUw5xvlfX1Q+OJ5vod+wO1w6pBjLFiCNC+xTQFjkDg8AQQ6DM1oSXqSKD3A4lon0R7ifHhd+3z12Xy9QpmNeGIJ0JHqbviycfByYRGDbJ7A/EdB9LyCd4FT1yJD4S3wb8gaCf+upfJLzyoI5+Tz30MHGXgh59ZCbhYCHNCuE1/QX+RIx68zaxRjfG9CLi2pX33ok+5EDgXAQT6TO1piXpEjI+F+KHvZiuTr1cwexaBXmKTHwQg1HdX/MIDHk0McH8gxClXIrQgtJAPyAfKAz4WrjDopY4fCbhY0D/6i/1XmKsNzpqvLdY+RiYnHHHOTvsStxCAwFoEEOjXIhnZUaL2A40RkX7KcdmKiij8a+KHoQr3uGT3FAM+XhCiEaIRonl1B39B0Fn9KAFOk3y+I8zTXyLMx/nAx0TJgz1824yAxtWKEfIF+UKxkGv8UEb+aebnqddPbXb3jReEQD/Oh6MQgMC5CSDQZ2pfG/iNiPNDK+bj/WYrk695zCLQr8nVYgBhFmEWYRZhlle72EO6XBPp3BN17LNiUzHgRRsevNs9nYuHjaPWHJxh67AEFA+54o37m1fNuRhQfCne9r9hyhfo92c034Ny2ne+71wBAQiURQCBPlN7WKKOBHrfUUf7QkE+ddxsZfK1a7bpuIM//Uz+UFX05L1+2l3/cJWefMvv+vPzj1p1ynFO+R+1elQvv9n+KertFttyJ7+r5z08p77O6uZtpX7UKr7O2Yiune2LlbraRshSg/5w4Kd97jxtc7wdGIsJfIgPxQL3B/cH+YB8QD641oMSf8+vNjLD0JEJuFgI+4Bwm/EB44Mc8eBt7n7TINDnaALXtmW0b47aYRMCENiSAAJ9JtqWqEfE+FCYH9s2W5l8NbPvZ3V3HUyolDfCdvjjqhLg7bTmuvCcqhpZQT+xnFqgrzu81rYE9a6I/nrcqlv40MCVEX5PCvTpQYq3FT8EaK53bfHJF+O54obFACvoWUEfrMiRuOTiQ9tMLJlYEg/cD+SDawnPtPfn9rZx1IpjM0wdl4Digf6S/nKL/Kl4m37HvKvX417Pyxvx935/VK93ZCGY375fj+D8e/V4dk+u57f1vFr++E+b0Ee23dcx+3Lm/awetkiuX25t9V15/+w858fAuU2Z7XzbWXhXr2dYv5uf57tFfN3/+ufd7vfqIV/Dk8fqFrELL0tti2fqGPsgAAEIzCGAQD+H1oxzlajd5yfx/dNx2ZpR/Fen1h13V/h2hnrit61Wd+c2gnkohvvShwX6yeUEHWenQr39w2XZdb1rmnqlVsvr4UJYp8T1dTUf/on52NjGfFiwoRjw8cSfwpsYDQ8mVltMrFQG8Ua8KRbcJ/FAPBAPn4VxMSrhfvE+LBiLcel5CLhYCGMy3Ca/07/liAdvc9ItpMVo9+r+eFav1ysQp6O/Im/mp06EdvadiP8IhP2OyP1+Va9Xsxjv/qiezq7719Xxux7G9h+1fVeWL+9Rl3vz5bYCeqdcJ68/W//qcltRPz5XDwXC/Xq40OFxj1hIk3C+OVG+8dUvPnRs4sl6XLcxdl0qvW/i0TvADghAAAIzCSDQzwQ29XRL1IdZQT8sctedaiTcaxW876DjDtJRGrI3tF+dd1CO7zgTthMr9tVxd1b/h43VdMJt3zzsh/fercgPxfsZvoTFrrVt8cQKelbQIwx2JtVMpJlIu/woEZB4IB6IB+6HVD6wcdRaAzPsHJqA4oF8Qb5I5QvtWys+FG9TbhqJ2e2ctblKc+/wgETm+C+/dW642Mybaea/vf0Dng3Yl4+uXqGQXg2V+35V796DgAFfmjJbu0OLAbs+m08hn7DOMaOBug3WoVtc59uc9u1cyBcIQAACEQEE+gjIWl8tUUcCvdv/acV8fNxsreVc0k7TSTZPxFVm+xkI583146L4kAA+oxzfcU4T6J1L1jH7OkT+Np1w22cP+VdXrrfKf6YvScQLdrbtwEBag2b36bjw/VgrGGkv2ksxwP1L/lIsuE/igXjIHQ8+xhaMxbj0PARcLIQ5J9wmH5GPc8SDt/nxFpIY7V5n867enX+v+lUyobjezG9bMVsFaBV+NB/WArrQhi5JfQ7ZlxDfTqybq4fKTRkfOLdXps67V8/B5f46J65vXa40gg6nXjnycdyWzgo/XdtOa9/wKrYhAAEI9Akg0PeZrLLHEnUk0Mfi+5TvZmsVz4aMjAvWvavUqTV/UtfrnzUA6B2YUY4vY7pAbz5q0NBbAR/+SOy4H6UK9Jq8+kEAr7oxcR4eCDu6N5hYM7EmH5APyAc8CFQMKB+4T79tg0U2rkxA8aD4iOOF73UOgc86/ani7fM918xPm3yl6zqfobiu+XjvnelDInNjP7Qx5tSg/aF59FC5rhD3Hvpn9fSvnnGvytErcSJRPVVm+J579/qap3vJbvjfh3o1Njt/aZ8qx5scq0NYZrut9mn3sAUBCEDgOwII9N9x+3iVErX7HBPhpxyXrY+FLjqh6YwmddhhJzjUiX3ouKeU4zvOLwR6W00fXNt0wuHzgp4Ib/wSvi/wxcwu2FAM+HhBmEeY51VHPga4H9aZOCJEIES4GOB+4n5SLjhrPPgYXzAW49LzEHCxEOa8cPus8X/2+7v0+k3LP+0cu7+CvllRH96Gs0Xm1n5X4A6NBtuD9hNzZX/ZgC7Q+QHb+t7TPdh5payzMVhm5QX+8Adp2+cSH+rV2ESgD9qWTQhAoEgCCPSZmkWdzpg4P/WY2crkq5nVyvNQxZbYHeyrhe1A/E5eNyL4J89vXlETlFN30EE5crS53v5MzX8Pn74nBgdNxxyat3fMdXdWT/8L86E9DRYm+CIfV/60GECYRZhFSOtMqplII6y6/Fj6xBz/WNGtGCBe97lfbRy18vgMc8ckoHjgftznfrxaPlS8fb5bEnPYsYsGxewhOx+E7LisQftzBHr5cq8enVfUaH9qzh292z7y690T3AdsNdfxipsIIF8hAIFiCSDQZ2oa64ijV9z4gWC0LxTqU8fNViZfu2abDjf807pQwB7oqNXxhaeaAO5txeL2h3KcU76s+Dr/xKByv8huAr0eIoQ+h6+3MVvhK25U64QfqdX9M3yR5TU/FQM+PlhBb2IcPJhYaZLnPokH4oF4QAhXDJAPyAeKBfUPPibWHJxh67AEXCyEOSLcVrzE8cN3+hfFwDfx4q+ZcMdoTh3Oc+0y/056+zay2nxIsB7aH9gMNwfm/dXgq2xT9pu5dm9+3bxTf2DOnqy/+dbYDISHegFhVx/wp7811480hcG6pepgBSc3XNtObd+kAXZCAAIQaAgg0GcKBUvUI2J8KMyPbZutTL5itnwCFgOsoGcFPUJ0Z1LNRJoHE35SxINLHlzSP9I/jvSPNo4qf8h3Lg8bESzQ0Yqon+KB/oMHeRLdc44nFW/Tgl+C8q26P57V8/WqXv7d7Xc//u0I11+IzBKyb3f3Hvh7dR+7OQft9wXyum5pcVtluvq8Xq/q+dT7552w/WEFvf9Leednfa1jodfcdF1vud3ce+r9u+5rZo5/h5tzdrBu6TqMtd289h2zxDEIQODqBBDoM0WAErX7/CS+fzouW5lcxewBCCgGfDwhRCFEIUQhRI0IUZpski8QHhQLOYUHlUG8EW+KhVLjzcfoAcZ853FxSMTbv4YuFsKcFW6XGr+l31/4N/4XBvPyz7t6OfE8/Ovw+6N6dl4R863IrJXr9T3QE67D23NQxB66t4fE7Xf1fLRi+e1Wv+6mFu4/CPTVRBbe77qckNs9xc2dO1i3oTqEYLrblk+6u/kGAQhAYDYBBPrZyKZdYImaFfTTgHHWKAGLJ4RZhFmE2c6kmok0K+j9pJcHlzy4pH+kfxzpH20cNTra4mBLYEiAa8/4tOVf1dF7rcWnq7Y5rnig/+DB4hYPFhRv20Q3pWxNgPbdmjjlQeC8BBDoM7WtJepIoPcDwWhfuII+ddxsZfIVs+UTUAz4+ECIQohCiEKIGhGiNNkkXyA8KBZ4kMWDLPIB7wieN9pdLtDPK2/bszWuVo7k/qC/VCzk6i99jG0b5pS2EQHLJxuVRzEQgMB5CSDQZ2pbS9QjYnwozI9tm61MvmK2fAIWAwizCLMIs6ygd69O40GdMXD5ER7jf1oPH/goBq56v9g4qqghXyOCB6+x6LxT2b97+VbdolXo9Y9IRj94qB9tHLLl6u1f6VC/TkLvhK65dG3pRyrFLD6nPu7sBP53HA/2N/50DhfQBmHddG+4T7ef7+RLxcBa8aB4KyD0cSEDAdo3A1RMQuCiBBDoMzW8ErXv2EdE+inHZSuTq5g9AAHFgI8XhDmbPMGDiaQmUUysERbIB+QD8gHCmmIglQ/8vlLGfBLfQ+U68U5kieV2WnNd573RE23pncuOQ3v90PuWh1fQyydnx/wS16m+6PydPp3vPh5Y+OLH1CELxlN5xlOe8U7xTrF5CVg+yVsM1iEAgQsQQKDP1MiWqGNx/lc9IHz8ulXvX7fOj788/kz/oKzZyuQrZssnYDHARIKJBCu8OpNqJpJ5JpISueALX9f/EA8I34qBo8aDjaMKGfIlfxzRL3KPV8yHAnqzHa2on2yreQDQE9WT+z8L9K3I30Kd7Et7yS5bioejxvPR78er+a942yXYKTQ7Ado3O2IKgMBlCCDQZ2pqS9SRQK/9tx/NL6f/uFWPn12hPn7dja7J5CpmD0BAMeA+Nah1n3yHB/GAcKYYIB+QDxQL9A/0j+SDfj7wTIoY830Sv+vX0JirWpXuV313X0dT6TUzPdW9qtpX0TSWvBAfX1+5E/2Coa7g/snHhJ05vljl9tlwsRDeI+E2+ZP8mSMevM19wp1SMxNwbUv7ZoaMeQhchAACfaaGtkQdCfRVs4LeHX/+E6yY/6cR6X/cqnd0jdnK5CtmyydgMcAKelbQ82CmM6lmIs1E2uVHhGkeVCkGiAfuB8VC2D/YOKqIIV8jfjeijnxrPyOBXivr3fk9IX6Gra0E+hn12qs5WtbcL6n7RfscJ22H95P2cXwaH8XbXvFOuXkJ0L55+WIdAlcigECfqbWVqP3AJRTcG4H+3rzOJjz+bFbVv4LzO3Yy+YrZ8gl04oB30Ntkwd8/8IAHD658DHA/TJsoIyzUYj7xQrzoXriK8OZjvogh3/Dq9KRw7aX/AAAgAElEQVR7zSto7ve7f0Dd1ehn2NpKoO86mKzS3jtdLIQ5MNy+yv1wtft/7/qWk3/2vvvOV77lk/NVjRpBAAIbE0CgzwTcEnUgtvtX10QCffg6m5RA746brUy+YrZ8AhYDCJEIkayg70yqmUizgt7lx70n3pTPCn7FAPFY5v1o46gihnzpd8mnXWsEeP/e+fB99Dp7hq3sAv0MX+T+Tp+KB+7XMu/Xs+VTxdtO4U6xmQnQvpkBYx4CFyKAQJ+psS1RRwK99msFPQJ9pgY4mVnFjfvUoNV98h0exAPCoGKAfEA+UCzQP9A/kg/6+cAzKWV8qPfKR6vN/Xvjg331j64G73tPXZfa518tf+++EmeWQD8sttfvtg98CplO9SW8ZodtFwvhPRJukz/JnzniwdvcIdYpMj8B17a0b37OlACBKxBAoM/UypaoI4Fe76BHoM8E/qRmLZ5YQc8Keh7MdCbVTKSZSPtJEa+6soe38OgLszy44EGmjaOKGicm3h8fiPOVXm3zfHe8rgXyWxWeaj8WG77/vXtCVdtLCOuNqN79kdj2x2Nrdu11owK99/RDvTq12eeL4oF8Sb7con9QvO0T7ZSamwDtm5sw9iFwHQII9JnaWonaD/xCkT56xU14PPWKm46dTL5itnwCnThAiEKI4kEND2p4UMODGv6iyvoCHtTxoM6Ppz+Mj/w55Q/58HADAhpXS5ydEj86l3xDvvkmXsg/G9zYOxVh+WSn8ikWAhA4DwEE+kxtaYk6FOfddiTQ84qbTA1wMrMWTwizCLMIswizCLMIsx+ESIQkVowrBrwoRLz4fsOzONn4kOp8R0Djau4PVtArV+Z88KJ4+y5auap0ArRv6S2EfxA4DgEE+kxtZYk6Eui1n1fcZAJ/UrOKG/e5xUBSZVAevBULOScuKoN4I94UC8QbKxTJB+SDtfOBj6mTjhOp1jwCLhbCHBNu0//Q/+SIB29zXphy9kEIuLalfQ/SWLgJgcIJINBnaiBL1JFAH66Yn7pttjL5itnyCVgMsIKeFfSsoO9MqplIM5H2kyJWCNvDW3ggbK8tbJ/Bno2jyh/y4eEGBBQP5Evy5Rb5TfG2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuB34hIP+W4bGVyFbMHIKAY8PGCEIUQxYMaHtTwoIYHNfxFlfUFPKjjQd2U8ZE/5wBjPlzMT0DjaomzU+JH55JvyDffxAv5J/99vVcJlk/2coByIQCB0xBAoM/UlJaoR8R5VtBngn9CsxZPCLMIswizCLMIswizPKi1GPCiBzzg8WF8ZOOoE44RqdJ8AooH8gcr6Ld48KJ4mx+pXHEEArTvEVoJHyFwDAII9JnayRJ1JND7gWC0LxTqU8fNViZfMVs+AcWAjw+ECISID0KEJhvECxNPxQIr/ljxRz4gH1w9H/h7oPwhHx5uQMDFQpgTw236S/rLHPHgbW4Q2xSxPQHXtrTv9twpEQJnJIBAn6lVLVGPiPGhMD+2bbYy+YrZ8glYDCDMenHeD4J4UMGDCu4H7gf+oqQjMiEsISzRP6YfxNg4qvwhHx5uQEDxwP2Svl/0MA8+6/BRvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfmAzItJPOS5bmVzF7AEIKAZ8vCBMI0wjTCNMI0wjTPOqI+sLeDDBg4kp4yN/zgHGfLiYn4DG1QjR/4/x1EbjKfJP/vt6rxIsn+zlAOVCAAKnIYBAn6kpLVGPiPNjq+bDY2Yrk6+YLZ+AxQDCLBOJjSYSmrQifCF8ufxDPNQiBvcD9wP3wzHzgY2jyh/y4eEGBBQP3M/HvJ81JjlK+yneNghtitiBAO27A3SKhMBJCSDQZ2pYS9SRQO8HEtG+WIwPv7tts5XJV8yWT0Ax4OOHFfQmFsKDiZUmaQinCKfkA/IB+YAHSYqBVD7w+8of8uHhBgRcLIQxEm4znmA8kSMevM0NYpsitifg2pb23Z47JULgjAQQ6DO1qiXqETE+FuKHvputTL5itnwCFgOsoGcFPSvoO5NqJtJMpP2kiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+DBrh7q5RxPKt42CG2K2IEA7bsDdIqEwEkJINBnalglaj/wGxHppxyXrUyuYvYABBQDPl4QohCiEKIQokaEKE02yRcID4qFnMKDyiDeiDfFQqnx5mP0AGM+XMxPwMVCmLPC7VLjt/T7C//G/4KJ/JP/vt6rBMsnezlAuRCAwGkIINBnakpL1CPi/NCK+Xi/2crkK2bLJ2AxgDCLMIsw25lUM5FmBb3LjwgD48IAfOCjGLjq/WLjqPKHfHi4AQHFw1Xvh6vng63rr3jbILQpYgcCtO8O0CkSAiclgECfqWEtUUcCvR8IRvtCQT513Gxl8hWz5RNQDPj4YAW9iXHwQJjUJMt9Eg/EA/GAEK0YIB+QDxQL6h98TJQ/5MPDDQi4WAhzRLiteInjh+/0L4qBb+LFX7NBbFPE9gRc29K+23OnRAickQACfaZWtUQ9IsaHwvzYttnK5CtmyydgMcAKelbQI0R3JtVMpHkw4SdFPLjkwSX9I/3jSP9o46jyh3x4uAEBxQP9Bw/yJLrnHE8q3jYIbYrYgQDtuwN0ioTASQkg0GdqWCVqP/AbEemnHJetTK5i9gAEFAM+XhCiEKIQohCiRoQoTTbJFwgPioWcwoPKIN6IN8VCqfHmY/QAYz5czE/AxUKYs8LtUuO39PsL/8b/woD8k/++3qsEyyd7OUC5EIDAaQgg0GdqSkvUI+L82Kr58JjZyuQrZssnYDGAMIswizDbmVQzkWYFvcuPCAPjwgB84KMYuOr9YuOo8od8eLgBAcXDVe+Hq+eDreuveNsgtCliBwK07w7QKRICJyWAQJ+pYS1RRwK9HwhG+2IxPvzuts1WJl8xWz4BxYCPH1bQmxgHD4RJTbLcJ/FAPBAPCNGKAfIB+UCxoP7Bx0T5Qz483ICAi4UwR4Tbipc4fvhO/6IY+CZe/DUbxDZFbE/AtS3tuz13SoTAGQkg0GdqVUvUI2K8E98fLqH/uFXvkfPMViZfMVs+AYsBVtCzgh4hujOpZiLNgwk/KeLBJQ8u6R/pH0f6RxtHlT/kw8MNCCge6D94kCfRPed4UvG2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuB3yfxfUSg79jJ5CtmyyfQiQOEKIQohCiEqBEhSpNN3/+QL8gX5AvyBfnCP9j1ObH8IR8ebkBA42r6y3pVPOOF/A8qyD8b3Ng7FWH5ZKfyKRYCEDgPAQT6TG1piXpEnGcFfSb4JzRr8YTQgtCC0MIKet65bqJ7zhVvCDcIN8TXef5Cx8ZRJxwjUqX5BBQP7lO5nvv9PPe72rSU9lW8zY9UrjgCAdr3CK2EjxA4BgEE+kztZIk6Euj9QOH/btXrZ/tueZ2rT95Bn6lRDmxWseHjhxWxNpmCBxNLTcKYWDOxJh+QD8gHvCNaMZDKB37fgceCuL4eARcLYYyE24wnGE/kiAdvc70QxlJBBFzb0r4FNQiuQODABBDoMzWeJepIoDfx/Z9b9fp1q+7NO+ifv+rvr39ulZ3TXGu2MvmK2fIJWAywgp4V9Kyg70yqmUgzkfaTIh5c8uCS/pH+caR/tHFU+UM+PNyAgOKB/oMHu3qol3M8qXjbILQpYgcCtO8O0CkSAiclgECfqWGVqP3Ab0ik/79mFT3voM/UCucx24knhCiEKIQohKgRIUqTTd//kC/IF+QL8gX5wj/Y9TnxPENDarKAgMbV9Je8yiynMB/GF/lnwQ1b+KWWTwr3E/cgAIHyCSDQZ2ojS9Qj4jzvoM8E/4RmLZ4QWhBaEFpYQc87c01032pirUk25fEXG15k4cGX3YNH4WHjqBOOEanSfAKKh6PEr/og/D3min/F2/xI5YojEKB9j9BK+AiBYxBAoM/UTpaoI4HeD6yCfY/mFTfvZl983In4ZiuTr5gtn4BiwMcHwsDhhAEmVqzQQthF2CV/H1NYIX+fJ3/7e7D8IR8ebkBA42ru7/Pc32rLUsdb5J8NbuydirB8slP5FAsBCJyHAAJ9pra0RB2I8fG75VlBnwn+Cc1aPLGCnhX0rKBnBT0r6O0hXakT8dKFAvyrRSni5zoPzmwcdcIxIlWaT0Dx4D7Jh+RDxUCueFC8zY9UrjgCAdr3CK2EjxA4BgEE+kztpETtO/oRkd6fxzvoM7XCecx24okV9DaZ8vcXPODBgysfA9wPCC0SGRCeryM8q825/z/f/57ReYaG1GQBARcL4T0TbpM/yZ854sHbXBCzXFouAde2tG+57YNnEDgSAQT6TK1liXpEnHcr6J8/6oT+GjnPbGXyFbPlE7AYQIhEiGQFfWdSzUSaibSfFPGgjgd19I/0jyP9o42jyh/y4eEGBBQP9B+fH2zpISDjre/HW4q3DUKbInYgQPvuAJ0iIXBSAgj0mRrWEnUkvPuBYLDv9bN5x/yPW/VotuNX4ZitTL5itnwCigEfPwhRCFEIUQhRI0KUJtPkC4QHxQLCyvfCihhyPx3/fvJtWP6QDw83IOBiIbynw23yJfkyRzx4mxvENkVsT8C1Le27PXdKhMAZCSDQZ2pVS9SBGB8L7/r+aFbRu2vuf94q7den2crkK2bLJ2AxgDCLMIsw25lUM5FmIu3yo0RU4oF4IB64H1L5wMZR5Q/58HADAooH8gX5IpUvtG+t+FC8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStS+Yx8R6accl61MrmL2AAQUAz5eWEFvYhw8mFhpEuU+iQfigXjgx/4UA+QD8oFiQf2Dj4kDjPlwMT8BFwthjgi3FS9x/PCd/kUx8E28+GvyhzYl7EDAtS3tuwN4ioTACQkg0GdqVEvUI+K8Vsh/+jRbmXzFbPkELAZYQc8KeoTozqSaiTQPJvykiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+BBnkT3nONJxdsGoU0ROxCgfXeATpEQOCkBBPpMDWuJOhLo/UAw2hcK9KnjZiuTr5gtn4BiwMcHQhRCFEIUQtSIEKXJJvkC4UGxkFN4UBnEG/GmWCg13nyMlj/kw8MNCLhYCHNWuF1q/JZ+f+Hf+F8YkH82uLF3KsLyyU7lUywEIHAeAgj0mdrSEvWIGB8K82PbZiuTr5gtn4DFAMIswizCbGdSzUSaFfQuPyIMjAsD8IGPYuCq94uNo8of8uHhBgQUD1e9H66eD7auv+Jtg9CmiB0I0L47QKdICJyUAAJ9poZVovYDvxGRfspx2crkKmYPQEAx4OOFFfQmxsEDYVKTLPdJPBAPxANCtGKAfEA+UCyof/AxcYAxHy7mJ+BiIcwR4bbiJY4fvtO/KAa+iRd/Tf7QpoQdCLi2pX13AE+REDghAQT6TI1qiXpEnB9bNR8eM1uZfMVs+QQsBlhBzwp6hOjOpJqJNA8m/KSIB5c8uKR/pH8c6R9tHFX+kA8PNyCgeKD/4EGeRPec40nF2wahTRE7EKB9d4BOkRA4KQEE+kwNa4k6Euj9QDDaF4vx4Xe3bbYy+YrZ8gkoBnz8IEQhRCFEIUSNCFGabJIvEB4UCzmFB5VBvBFvioVS483HaPlDPjzcgICLhTBnhdulxm/p9xf+jf+FAflngxt7pyIsn+xUPsVCAALnIYBAn6ktLVGPiPGxED/03Wxl8hWz5ROwGECYRZhFmO1MqplIs4Le5UeEgXFhAD7wUQxc9X6xcVT5Qz483ICA4uGq98PV88HW9Ve8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStR+4Dci0k85LluZXMXsAQgoBny8sILexDh4IExqkuU+iQfigXhAiFYMkA/IB4oF9Q8+Jg4w5sPF/ARcLIQ5ItxWvMTxw3f6F8XAN/Hir8kf2pSwAwHXtrTvDuApEgInJIBAn6lRLVGPiPNDK+bj/WYrk6+YLZ+AxQAr6FlBjxDdmVQzkebBhJ8U8eCSB5f0j/SPI/2jjaPKH/Lh4QYEFA/0HzzIk+ieczypeNsgtCliBwK07w7QKRICJyWAQJ+pYS1RRwK9HwhG+0JBPnXcbGXyFbPlE1AM+PhAiEKIQohCiBoRojTZJF8gPCgWcgoPKoN4I94UC6XGm4/R8od8eLgBARcLYc4Kt0uN39LvL/wb/wsD8s8GN/ZORVg+2al8ioUABM5DAIE+U1taoh4R40NhfmzbbGXyFbPlE7AYQJhFmEWY7UyqmUizgt7lR4SBcWEAPvBRDFz1frFxVPlDPjzcgIDi4ar3w9Xzwdb1V7xtENoUsQMB2ncH6BQJgZMSQKDP1LBK1H7gNyLSTzkuW5lcxewBCCgGfLywgt7EOHggTGqS5T6JB+KBeECIVgyQD8gHigX1Dz4mDjDmw8X8BFwshDki3Fa8xPHDd/oXxcA38eKvyR/alLADAde2tO8O4CkSAickgECfqVEtUY+I82Or5sNjZiuTr5gtn4DFACvoWUGPEN2ZVDOR5sGEnxTx4JIHl/SP9I8j/aONo8of8uHhBgQUD/QfPMiT6J5zPKl42yC0KWIHArTvDtApEgInJYBAn6lhLVFHAr0fCEb7YjE+/O62zVYmXzFbPgHFgI8fhCiEKIQohKgRIUqTTfIFwoNiIafwoDKIN+JNsVBqvPkYLX/Ih4cbEHCxEOascLvU+C39/sK/8b8wIP9scGPvVITlk53Kp1gIQOA8BBDoM7WlJeoRMT4W4oe+m61MvmK2fAIWAwizCLMIs51JNRNpVtC7/IgwMC4MwAc+ioGr3i82jip/yIeHGxBQPFz1frh6Pti6/oq3DUKbInYgQPvuAJ0iIXBSAgj0mRpWidoP/EZE+inHZSuTq5g9AAHFgI8XVtCbGAcPhElNstwn8UA8EA8I0YoB8gH5QLGg/sHHxAHGfLiYn4CLhTBHhNuKlzh++E7/ohj4Jl78NflDmxJ2IODalvbdATxFQuCEBBDoMzWqJeoRcX5oxXy832xl8hWz5ROwGGAFPSvoEaI7k2om0jyY8JMiHlzy4JL+kf5xpH+0cVT5Qz483ICA4oH+gwd5Et1zjicVbxuENkXsQID23QE6RULgpAQQ6DM1rCXqSKD3A8FoXyjIp46brUy+YrZ8AooBHx8IUQhRCFEIUSNClCab5AuEB8VCTuFBZRBvxJtiodR48zFa/pAPDzcg4GIhzFnhdqnxW/r9hX/jf2FA/tngxt6pCMsnO5VPsRCAwHkIINBnaktL1CNifCjMj22brUy+YrZ8AhYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaOKn/Ih4cbEFA8XPV+uHo+2Lr+ircNQpsidiBA++4AnSIhcFICCPSZGlaJ2g/8RkT6KcdlK5OrmD0AAcWAjxdW0JsYBw+ESU2y3CfxQDwQDwjRigHyAflAsaD+wcfEAcZ8uJifgIuFMEeE24qXOH74Tv+iGPgmXvw1+UObEnYg4NqW9t0BPEVC4IQEbkoofNaJFQ5wIAaIgb1iYMnAX9e6T+c/35lIKgaIh/z3w145g3Lpr4gBYoAYWBYD6ivnjJ9gvow5/OBHDBADR4uBE2rBVKlAAgj0zRPPoyUI/KVTIwbOGQPfTBR1jYsJbc+ZaOoaroefYoH4mf6gi1x8zlxMu9KuxMD5Y0B93jfjH+Lj/PFBG9PGxAAxoBgoUMvFpRMS4BU3J2xUqgQBCByLAB3/sdoLbyEQEuD+DWmwDQEIQKB8Akvz9tLryyeEhxCAAAQg4AiQ74mDLQkg0G9Jm7IgAAEIJAjQ8SegsAsCByHA/XuQhsJNCEAAAg2BpXl76fU0BAQgAAEIHIMA+f4Y7XQWLxHoz9KS1AMCEDgsATr+wzYdjkOAlTXEAAQgAIGDEVg67lp6/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+Odlxei9ejcsnn/ny3tlL72qNsQQACKxGg418JJGYgsAMB7t8doF+tyNR4LLXvalyoLwS+JLA0by+9/ku3uQwC8wmk+orUvvmWuQIClyBAvr9EMxdTSQT6NZri/aoe97sXuP0NfL9Xj1cgdK9RRm4bqY46tS+3Hyez/37WcdF58HGyOlKd5QTo+JczxAIE9iLA/bsX+YnlMkabCOp6pzFGu16bq8ZL8/bS6+UHn4UToP8ouoHI4UU3z2mcI9+fpikPUREE+qXN9HpU99utXn3+eFSPR/A9XI2+tJzc16fE+NS+3H58Zf9VPVwb3J9VaY9FGDh81aCXu4iO/3JNToVPRID7t+DGZIxWQOMwRiugEXAhIrA0by+9PnKHryUSoP8osVU6PjHP7uDgSyYC5PtMYDGbJIBAn8Qyfefr4cT5exVr8a7DONSq6ZQYn9o3Hc2GZ5Y7+dsQAkUdmAAd/4EbD9cvT4D7t9wQYIxWQtswRiuhFfChS2Bp3l56fdcbvpVIgP6jxFbBJwhsT4B8vz3zK5eIQL+o9d/V8+4E+kf1WmSngItTYnxqXwGu9l1g8tdnwp4jEaDjP1Jr4SsEugS4fw+uuOcAABK7SURBVLs8yvnGGK2MtmCMVkY74EVIYGneXnp96AvbJRKg/yixVfAJAnsQIN/vQf26ZSLQL2p7dd636jFJoX9Xr8fdXonjbvb7/VH1XlffCOPO5jv48zq3Ut/ebf9+Vg//cKBewf+Il/BbveaV2Vn1PyjQT7RpPsQbE65vyu69tub9rPk1r7OpVzfUrxhS8vSfnQaZUJ5zcYx7ku+7ej3bVxrV7fnsPqwZYxhdexv67YLZfsW8+V46AcVu6X7iHwQg0CfA/dtnUsYexmiKzeRYc7CRJoyZGKO19BijtSwOtKV741uXl17/bblctxUB+g/F+OT+YywXSuyYpF+8a/3DdI4RraMps6NfVBPm5z6M+ucxF9/q/jpWOboXjuU13h6VAAL90pbTJMWJ7Y/XyDvQ1dHfq/vjWb1er0DcjV6RI5vND8/e/bvt2x+hvT+a7fund97PL7PTwQ10evVfDUyoR5LtdJ8kvodae+/PDd+v6vWSaP+ono6r+2cvo59engR61zm7ROwGJI/ggUqHjdfz6wcDnfa8p9uye618cu/Nv/vfLeiUE1bYMYzj4YNfSezsLJoAHX/RzYNzEBglwP07imffg+o/GaMlX8fYbxyNTz6P8RijNfQUYxPHjn3m7NmDwNK8vfT6PepMmTMJ6N6m/5jWf4iXcuGX+oW9V/6ueX27KLE7n27nyOF+9U2j8/NKfR1z8Zl3xSVPJ99fstl3qzQC/Qrou6vcnVD/DATiugB1NrH2WmlFeHhAHVz0bnvZcEki7IjMRvQjqTo/NO29GSmzY7fxI9w3y2aC7bzrmz+L1iuEEv7URQz/+fSs8ga4p/k2HXvEvFflhM/y6dZrGNU3LfL3futA7fjJh55T7CiNAB1/aS2CPxCYToD79/+3d2/XjcJAAEBTVwpKPa4mzaQY7wF7bCwesSIWD/h+7CEEhIYrGAnZYZ+3esWexmjn820cMxp3PLZIjE9Gu8V442FDjFmur3mcGO9cjm6MdvvOyCO3tRcKtObt1vIvPHVVVwjoP57vP25fKGucvzj/fJ9/Rklzph8Z9TvPPZ9HX+dZvOJmeONd5fs3bvwXnLoJ+tXQyz+T6l5HEwePzqJ7nc3P+efh3/flVTXDSdZRZ3M9zuQDUrctPgUevgt/hTpHcVQeM07/tvxD+WsMH92n8B/dp9ynib9SmOm0w6V/jVCDexwnPijozyfMP8+n+9f1b2d6+2HO8OFYt73PMWAYfigSA56H3z3EMGz3+7H8tB8BHf9+2kqkBEoB928pknHdGK1/LeLkGCrayxhtejwdPt3nHNe/sBy+9nA0zov9Y5xojBYimZatebu1fCYLsfwmoP/4vf+Y/jZ7L1s1fzHXFjP5dJR/Y7+l5/PYZzo3y/NzbfC+v5fv37ftX3HmJuhXV+868XgdTST++JbRxLvSu0nncuJ51NlEkNfj3Gf+rxumOpoV6hzFUXnMCPu2/Fv5+FO10TfIy+OOHjwr6xudb1Qw5Xv5RsHt/wHoXlVzmnjF0eiY15hGsV7ruu7/8In+6Bi/xBWbLXcjoOPfTVMJlMBIwP07Ikn8C2O00RcTb61VOWa6ljNG+7q8FnE4ad/bzIwdb95+eKVAa95uLf/Kc1f3XwX0H/P9x8IE/fnatzw1fxFt072H/nQ+9a/JGb7SN+ZWrvtNPSMP33M/+XzuWTyULZ8TkO+fc7LXOgIm6NdxHB0lHlgufdG9Ixh/g/76ze7hEaY6m357TQe3Qp2jOCqPOTynYfyf3SuAym+0Tzj0ZeIB5/JBxqhvL477OHCojHd0vnECEUMxKLhu7gYQt4n64s/6xt9+v8f0GOv1YNcYTNCH/Xssdfzv0c7O8pgC7t/9tasx2lSb3ccnxmhTf615n4AyRpu6fvb1u9a83Vp+X1qiHQroP4Yag59nn6OvfcvoIX7m+fr76/wZX2AcLYtn8dk6z/0E//Tz+b2v8yw+aD8/zgrI97M0NvwHARP0/wG1O+Rj5z3TAc3VPdvZ1HRwK9Q5iqPymKPzqy8ff2bWfTu9f8XN5Kth5jrayvpG5xsn8NxxuvcU9gl8OAAZHXP5WHG+D6+zGR2jLq7Y2zKvgI4/b9uIjMBvAu7f34TybTdGm2qT5fHJZInrX4waoxX/N1SPVe85Zex3/0egNW+3lv8/Z+WoWwjoP2aUZ59X/zJ/0b0qeDh9PpNPZ+u8xzh+Pp851rWIZ/G7nZ8uAvK9K2FLARP0LdrdO9X695sXB/kZTyZPJvso1n+bPFbu39B5mKTtN9d0cDPvyoxqnqlzotOrOo+oa7CsKh/vrIvXwVzjefjmUn/s+Y62qr6J872EPn/8wal1DXf5EGFxgv7+4c2ofW/XzfR/Ejvaf/Ld+I8RWduHgI5/H+0kSgJTAu7fKZUEvzNGe2yEctz3uLVfqxozGaNdBJvHjhMN4Vf/XaA1b7eW/+8nqII2Af3Ho98T/cf4r8bjEBPPx/2mqefr677x7B+H6J6xP7u/pn/+G/S3ohPP5/Ehy+jZ2rP4nc1PNwH5/kbhhw0ETNC3IMfDSf8O+cv70b6+4v3z5bdprh3Ox8f58+t0Pn1/n7/7d6vV/IdTNR1cd2KNdU4+dFQcc9L22fLRaT9OVkeHOpwD78/0K97l37XD5/nztsOz9S19MBKxDAYFfdt39ZzO39e2jD+ju1V9CWzi3aT3mD66d+P179ebu24q45o098vsAjr+7C0kPgLzAu7feZuXbjFGWx5rTjbOfXyyPFaNcZEx2vykVBgNxo6T5n75CoHWvN1a/hXnrM4KAf1Hff8xOW/QmV/7lYcH5O730zkynvXjGft0Gr7ypsinZZ3PPp9HTP0cjmfxijvjLXeV79+y2V920iboW+l/vs+nbkJ48I60y7fqh3+WFZX8nL+LfT8+v86nhz/hWpqQrevgLrU21Fl2enEa5yePedu//OH38rPf4roNmIoOuuto+0/WLxP1j5+I/15fH+HC+Z5Gn9qvcMziWuium9G10AVWFVdpbX0PAjr+PbSSGAlMC7h/p11S/NYY7fLqvbnxxWQj/T6+MUYbwBmjDTD282Nr3m4tvx+pN45U/1HXf8zmwtr5i59+biXusY+Py+tuLhP3xfP/qM7f+6/7FX2pp5zD8Sx+F/LTRSCuRR4EthAwQb+FsjoIECCwIKDjX8CxiUByAfdv8gYSHgECBAqB1rzdWr4IxyoBAgQIJBWQ75M2zEHDMkF/0IZ1WgQI7EdAx7+fthIpgVLA/VuKWCdAgEBugda83Vo+t47oCBAgQCAE5PuQsNxCwAT9FsrqIECAwIKAjn8BxyYCyQXcv8kbSHgECBAoBFrzdmv5IhyrBAgQIJBUQL5P2jAHDcsE/UEb1mkRILAfAR3/ftpKpARKAfdvKWKdAAECuQVa83Zr+dw6oiNAgACBEJDvQ8JyCwET9Fsoq4MAAQILAjr+BRybCCQXcP8mbyDhESBAoBBozdut5YtwrBIgQIBAUgH5PmnDHDQsE/QHbVinRYDAfgR0/PtpK5ESKAXcv6WIdQIECOQWaM3breVz64iOAAECBEJAvg8Jyy0ETNBvoawOAgQILAjo+BdwbCKQXMD9m7yBhEeAAIFCoDVvt5YvwrFKgAABAkkF5PukDXPQsEzQH7RhnRYBAvsR0PHvp61ESqAUcP+WItYJECCQW6A1b7eWz60jOgIECBAIAfk+JCy3EDBBv4WyOggQILAgoONfwLGJQHIB92/yBhIeAQIECoHWvN1avgjHKgECBAgkFZDvkzbMQcMyQX/QhnVaBAjsR0DHv5+2EimBUsD9W4pYJ0CAQG6B1rzdWj63jugIECBAIATk+5Cw3ELABP0WyuogQIDAgoCOfwHHJgLJBdy/yRtIeAQIECgEWvN2a/kiHKsECBAgkFRAvk/aMAcNywT9QRvWaREgsB8BHf9+2kqkBEoB928pYp0AAQK5BVrzdmv53DqiI0CAAIEQkO9DwnILARP0WyirgwABAgsCOv4FHJsIJBdw/yZvIOERIECgEGjN263li3CsEiBAgEBSAfk+acMcNCwT9AdtWKdFgMB+BHT8+2krkRIoBdy/pYh1AgQI5BZozdut5XPriI4AAQIEQkC+DwnLLQRM0G+hrA4CBAgsCOj4F3BsIpBcwP2bvIGER4AAgUKgNW+3li/CsUqAAAECSQXk+6QNc9CwTNAftGGdFgEC+xHQ8e+nrURKoBRw/5Yi1gkQIJBboDVvt5bPrSM6AgQIEAgB+T4kLLcQMEG/hbI6CBAgsCCg41/AsYlAcgH3b/IGEh4BAgQKgda83Vq+CMcqAQIECCQVkO+TNsxBwzJBf9CGdVoECOxHQMe/n7YSKYFSwP1bilgnQIBAboHWvN1aPreO6AgQIEAgBOT7kLDcQsAE/RbK6iBAgMCCgI5/AccmAskF3L/JG0h4BAgQKARa83Zr+SIcqwQIECCQVEC+T9owBw3LBP1BG9ZpESCwHwEd/37aSqQESgH3bylinQABArkFWvN2a/ncOqIjQIAAgRCQ70PCcgsBE/RbKKuDAAECCwI6/gUcmwgkF3D/Jm8g4REgQKAQaM3breWLcKwSIECAQFIB+T5pwxw0LBP0B21Yp0WAwH4EdPz7aSuREigF3L+liHUCBAjkFmjN263lc+uIjgABAgRCQL4PCcstBEzQb6GsDgIECCwI6PgXcGwikFzA/Zu8gYRHgACBQqA1b7eWL8KxSoAAAQJJBeT7pA1z0LBM0B+0YZ0WAQL7EdDx76etREqgFHD/liLWCRAgkFugNW+3ls+tIzoCBAgQCAH5PiQstxAwQb+FsjoIECCwIKDjX8CxiUByAfdv8gYSHgECBAqB1rzdWr4IxyoBAgQIJBWQ75M2zEHDMkF/0IZ1WgQI7EdAx7+fthIpgVLA/VuKWCdAgEBugda83Vo+t47oCBAgQCAE5PuQsNxCwAT9FsrqIECAwIKAjn8BxyYCyQXcv8kbSHgECBAoBFrzdmv5IhyrBAgQIJBUQL5P2jAHDcsE/UEb1mkRILAfAR3/ftpKpARKAfdvKWKdAAECuQVa83Zr+dw6oiNAgACBEJDvQ8JyCwET9Fsoq4MAAQILAjr+BRybCCQXcP8mbyDhESBAoBBozdut5YtwrBIgQIBAUgH5PmnDHDQsE/QHbVinRYDAfgR0/PtpK5ESKAXcv6WIdQIECOQWaM3breVz64iOAAECBEJAvg8Jyy0ETNBvoawOAgQILAjo+BdwbCKQXMD9m7yBhEeAAIFCoDVvt5YvwrFKgAABAkkF5PukDXPQsEzQH7RhnRYBAvsR0PHvp61ESqAUcP+WItYJECCQW6A1b7eWz60jOgIECBAIAfk+JCy3EDBBv4WyOggQILAgoONfwLGJQHIB92/yBhIeAQIECoHWvN1avgjHKgECBAgkFZDvkzbMQcMyQX/QhnVaBAjsR0DHv5+2EimBUsD9W4pYJ0CAQG6B1rzdWj63jugIECBAIATk+5Cw3ELABP0WyuogQIDAgoCOfwHHJgLJBdy/yRtIeAQIECgEWvN2a/kiHKsECBAgkFRAvk/aMAcN6yMuOMuPMwMGrgHXwCuvgYP2M06LwKEFXpkz1K3Pcg24BlwDf78G/to5Mf+7OTt2rgHXwB6vgb/2F8oRqBEwQf8hQe4xQYrZdXvEa6AmeduXAIEcAkfMRc5JH+sacA28wzXw117kHWycoxzgGnANuAbu18Bf+wvlCNQIeMVNjZZ9CRAgQIAAAQIECBAgQIAAAQIECBAgQIDASgIm6FeCdBgCBAgQIECAAAECBAgQIECAAAECBAgQIFAjYIK+Rsu+BAgQIECAAAECBAgQIECAAAECBAgQIEBgJQET9CtBOgwBAgQIECBAgAABAgQIECBAgAABAgQIEKgRMEFfo2VfAgQIECBAgAABAgQIECBAgAABAgQIECCwkoAJ+pUgHYYAAQIECBAgQIAAAQIECBAgQIAAAQIECNQImKCv0bIvAQIECBAgQIAAAQIECBAgQIAAAQIECBBYScAE/UqQDkOAAAECBAgQIECAAAECBAgQIECAAAECBGoETNDXaNmXAAECBAgQIECAAAECBAgQIECAAAECBAisJGCCfiVIhyFAgAABAgQIECBAgAABAgQIECBAgAABAjUCJuhrtOxLgAABAgQIECBAgAABAgQIECBAgAABAgRWEjBBvxKkwxAgQIAAAQIECBAgQIAAAQIECBAgQIAAgRoBE/Q1WvYlQIAAAQIECBAgQIAAAQIECBAgQIAAAQIrCZigXwnSYQgQIECAAAECBAgQIECAAAECBAgQIECAQI2ACfoaLfsSIECAAAECBAgQIECAAAECBAgQIECAAIGVBEzQrwTpMAQIECBAgAABAgQIECBAgAABAgQIECBAoEbgH6WiRri5sayzAAAAAElFTkSuQmCC[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABegAAAF1CAYAAACTcQoTAAAgAElEQVR4AeydPdKruNa2PZgTdNWegZMOO9kjOPEpRx2dCXS8M4edfVEP4CSO33l4MHwlwb0QQmAwCARcXbXbmJ+lpUuLJelGD75V/AcBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMDmBG6bl0iBEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIVAj0BAEEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0O8AnSIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgj0xAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYAcCCPQ7QKdICEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAACPTEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACENiBAAL9DtApEgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCAQE8MQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2IIBAvwN0ioQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIINATAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHQgg0GeCfrvdKv7BgBggBogBYoAYIAaIAWKAGCAGiAFigBg4VgysJRPQ7sdqd9qL9iIGiIHdYmCtjgc7XQK7NSgPBngwQgwQA8QAMUAMEAPEADFADBADxAAxQAx8HQPd2f3339AFEPuIAWKAGCAGJsXA910NV44REPzq/27V0n9ma6xAjkEAAhCAAAQgAAEIQAACEIAABCDwNYG1595r2/u6YlwIAQhAAAJFE+AVN5maxzriSKB3+8cE+9Rxs5XJV8xCAAIQgAAEIAABCEAAAhCAAASuTmDtuffa9q7ePtQfAhCAwFkJINBnalnriCOBfkycHzpmtjL5ilkIQAACEIAABCAAAQhAAAIQgMDVCaw9917b3tXbh/pDAAIQOCsBBPpMLauO2H0OCe9u/5TjspXJVcxCAAIQgAAEIAABCEAAAhCAAAQuT2Dtuffa9i7fQACAAAQgcFICCPSZGtY6YlbQZyKMWQhAAAIQgAAEIAABCEAAAhCAwHoEbB6/ksm17a3kFmYgAAEIQKAwAgj0mRrEOuJIoHf7566oN1uZfMUsBCAAAQhAAAIQgAAEIAABCEDg6gTWnnuvbe/q7UP9IQABCJyVAAJ9ppa1jjgS6MfE+aFjZiuTr5iFAAQgAAEIQAACEIAABCAAAQhcncDac++17V29fag/BCAAgbMSQKDP1LLqiN3nkPDu9k85LluZXMUsBCAAAQhAAAIQgAAEIAABCEDg8gTWnnuvbe/yDQQACEAAAiclgECfqWGtI2YFfSbCmIUABCAAAQhAAAIQgAAEIAABCKxHwObxK5lc295KbmEGAhCAAAQKI4BAn6lBrCOOBHq3f+6KerOVyVfMQgACEIAABCAAAQhAAAIQgAAErk5g7bn32vau3j7UHwIQgMBZCSDQZ2pZ64gjgX5MnB86ZrYy+YpZCEAAAhCAAAQgAAEIQAACEIDA1QmsPfde297V24f6QwACEDgrAQT6TC2rjth9Dgnvbv+U47KVyVXMQgACEIAABCAAAQhAAAIQgAAELk9g7bn32vYu30AAgAAEIHBSAgj0mRrWOmJW0GcijFkIQAACEIAABCAAAQhAAAIQgMB6BGwev5LJte2t5BZmIAABCECgMAII9JkaxDriSKB3++euqDdbmXzFLAQgAAEIQAACEIAABCAAAQhA4OoE1p57r23v6u1D/SEAAQiclQACfaaWtY44EujHxPmhY2Yrk6+YhQAEIAABCEAAAhCAAAQgAAEIXJ3A2nPvte1dvX2oPwQgAIGzEkCgz9Sy6ojd55Dw7vZPOS5bmVzFLAQgAAEIQAACEIAABCAAAQhA4PIE1p57r23v8g0EAAhAAAInJYBAn6lhrSNmBX0mwpiFAAQgAAEIQAACEIAABCAAAQisR8Dm8SuZXNveSm5hBgIQgAAECiOAQJ+pQawjjgR6t3/uinqzlclXzEIAAhCAAAQgAAEIQAACEIAABK5OYO2599r2rt4+1B8CEIDAWQkg0GdqWeuII4F+TJwfOma2MvmKWQhAAAIQgAAEIAABCEAAAhCAwNUJrD33Xtve1duH+kMAAhA4KwEE+kwtq47YfQ4J727/lOOylclVzEIAAhCAAAQgAAEIQAACEIAABC5PYO2599r2Lt9AAIAABCBwUgII9Jka1jpiVtBnIoxZCEAAAhCAAAS2IPB6uAUF9+r53qK0fGWcpR75CGEZAhCAAARsHr8SirXtreQWZiAAAQhAoDACCPSZGsQ64kigd/vnrqg3W5l8xSwEIAABCFyYwOvh/5rrHqqvqX0XRnTOqr+r590J74/qNVbB97O6327V7TF61piFMo6dpR5l0MQLCEAAAqclsPbce217pwVPxSAwRCA1L0ntG7qe/RA4CAEE+kwNZR1xJNB3xPl/bvWk9+dn0d7Z4z8IQAACELgYAYmKTiAN/93v1f3xrF5rrGhODXBT+y6Gfml13897/8HHUqOrXj9NoK9XnX8Q8Vf1K4+xs9QjDx2sQgACEICACGi8pe9LP9e2t9QfrofAqgSYqyzCWf58YVH1uHgmAVTfmcCmnq6O2H12RPlQsP+nEVxGBPqOnamFcx4EIAABCJyDgAa993v1eDzsn1/R3Aj2nZXv39Q6Jcan9n1jO/s1r+rhONyf1RrPKtZ0t/wB9wSBvom/chfPT2z/4uuxZuRhCwIQgAAElhDQ/HuJjfDate2FttmGwO4EmKssaoLy5wuLqsfFMwkg0M8ENvV064hDQT7eZgX9VJycBwEIQOCaBDToTSik71fz6pHbrUocns4rJcan9k23uOGZEwXaDT06TlETBPriK0P7F99EOAgBCEDgYARsHr+S32vbW8ktzEBgHQLMVdbhiBUIVFWFQJ8pDKwjjkR5t99W1CcE+s7x5lqzlclXzEIAAhCAQKEERga93uNGSP/4HvGx6qXE+NS+MRu7HUOg/R49Av337LgSAhCAAATOSmDtuffa9s7KnXodlABzlYM2HG6XSACBPlOrWEccCfQmzrv9CYG+cxyBPlPrYBYCEIDAQQh8GvRWElnjVfTv6v16VHf/I6B6f/29eoQ/BCsEKTE+tc+f/65ej3v9+yl6xc79MeNd+BOub8ruvbZGLJrX2dTvFFfdgs/OnxNMKM/VqynTXeq52fv+B5hV7+r1fEQcnt0fWx1jGF17c68wSv2gwGy/1KjR5/tVPR/1O/H9+MS3mWIn9X75OdzulQurON7uj9fAa4f67KbU38VdPba6V8+Xa7Kgza294h+znViPVWI7Ys5XCEAAAhA4JAGbx6/k/dr2VnILMxBYh4DG553xd2ha480DzFXGxt0ap7+f1cPmV8PzhHhcfLsNnJucL/THyvd7NM/wiPvnTRlTT5vrhG3I9lYEEOgzkVZH7D5TorvfxzvoM9HHLAQgAIGTEPg46K2q1LsLbd/9UT1fr+r1ageTvXfWpwaGqX32MKD5gVpn14TmWqQdp64B+ufrJb6GY/16X1DOu66Xfx+/1fMVPCyYXp4Eejeodf32/e7e998+iIiZyT//Q73icA98cyBGGbr35ut3BYJywgoHNqb6lebf/JWBf1d//TsG3Qc3sUA/l9u9une4BQ8u4vpYDM2svxfgXdw8qofj/KrcEwEf16u0v/n1OTbTjNkLAQhAAAJnIaB5/Fr1WdveWn5hBwKrEDjTXKUZu9u42//+lxaI3Kq7Fov4eUI73o3nCUvnYZPmGTZ2nTmm7ozZgzlIahHXKgGCkTkEEOjn0JpxrnXErKCfQY1TIQABCECgQ2DCoDcpBL9f1bv3q6kDr4NJCcmJfRps9jXX5l34vQOdmtiDhN5pyTpKVG7E44Q/tfWBOjn99lkPqCeVpwH5LRLZ5VvnR2gbAbuzr1tX/y3hs3y69ZxSfaPyZ/mV8CHgMDR5iF+PJB97LopFeGDIvypdH9leXH+r6jrtL7/CqvkiUnW2stmAAAQgAIEzErB5/EqVW9veSm5hBgLrEJgyVkqMid1Ci9LmKppTudXuoV6tcaK7lzvjadU9nhMsqtu0eYb51Bu8psfgQ3WrhuqwTnRgZSYBBPqZwKaebh1xJNC7/baiPvGKm85xXnEzFTfnQQACEDgnAQ2aeoOvtroaoHUGjO3hYEsro6MV06lBc2+fBovudTbv6t3596r/1DMenAYlV1rl0bxaZdL1En/d6hW/+vuZeGXKkEA7099efeV8ipn2uZXcvacgujCxgl7XRfybK5LtOMuvtuh2a6zM1LFm39R2GvSvfUDSxmWqvMDT5oFKe/7QXyG011R6ENCLvTn1mHNuWDbbEIAABCBwRgI2j1+pcmvbW8ktzEBgHQKnmauMjDsH6zg+tu0CHji3N5bWeWPzDJ2z5ZyiWxu+5SGAQJ+Ha/Oe1ECMj4R6veLG/2n2z/Hz6NQzNRJmIQABCJROYHBA2DouYbev4bv30D+rp//zzObVJv5VIdFgrjcwTA1QtRpj4L3fgwK6/Pzuev2JZ7ySRVaHBdqZ5aUY+EIGBsDh+yfdq2qeifet92wOPUxoatOc31ld3rOhmg/4pcP2OVZmysZa3EZiqCemf1N/VXCofnPqMedclcsnBCAAAQiclcDac++17Z2VO/U6KIHTzFVSY1e1STNW7E22UmNpXbNgHvZxnjE0/m3KzjKnUL34zEkAgT4TXXXE7tNWzMciPe+gz0QfsxCAAAROQuDjoFcDw+6fYro/Y/QPgL0gH4vqCwR69wNFndXzwWr6UeTtQHL69apb7X9vTOzLa+1217K3+yeV96UQ7h6AhD8UFf45rP6UtF0R3vrU9bUBl2UwPVam+Ibx0J6/jFtqktPaXl5/BduQzXb/53rMOVfl8gkBCEAAAmcloHn8WvVb295afmEHAqsQOM1cJTV2FaFmrNibjKTG0rWdRfOwptjheUY7dl0+ph6og6rO56YEEOgz4baOOBblw++JV9ykxHyzlclXzEIAAhCAQKEEPg16dbyzKlkDrXv16LyCRftDQXZgMNoTrAeunYxt/vX2lwHPZhB6i/z2ZQ8NUGeW16uvKjbNznuSuD5uS/VtBf2BtvGujduS9/ZqoSS7lI3UvtZab2uQW/uKm3YuM257Xv3lyRrtP+6XSuITAhCAAASuQWDtuffa9q7RCtTyMAQ0F2kHfF3Xdbz4ucrYuLsZb/bqmBpDat+CeViXYNWfZ6iM1NyoHYOvO6eInOJrFgII9FmwVoOvuHEdtInwCYG+c7wR8+nUMzUSZiEAAQiUTkCD2t6A0P/6p62S7x4eEi2bd8XHYm1KZE3sSwqo4udX1etL+nPW9aq3BvMpAdwXMzxAnVVeor51LYbtd2uZGLgnbOqVPZ0BszP0bq6PfpSqvwpfpU71y70Kv/4LhG6Z7+r1qH9Ed+hHYrvnN+XG7ax2if3Wu+Gj/Wlfvqn/Zw5z2n/OuSqZTwhAAAIQOCeBtefea9s7J3VqdVgCGrN3JyN1dXTsdqu6h8ucqwyPuxPjfF/D1Hh8hbr1gqFf/npj6lQdeg6wYyMCCPSZQFtHHK6Yj7cTAr2J98G5ZiuTr5iFAAQgAIFCCWhg695z3nuXvBNe3fvP+3/caIO2x7N6vV7V8xm+8iZabZEQktMD1GZweLtV98ezer5e1cu/474WepOCbgfr1Os1UOy+tkd16g7wWwH6dnfv2b9XdzthanljK2bkS8DMt4krp2brGOg1N1a0q3eKqwnXt+pmbSqh/Fb1GCZtOOMJvzqsgy+KIddunpFi4V7d7y6Ggrr5y+Zz0ziltn+3B0e9+qxW/7Z+iotF7R/49V1st/6wBQEIQAACxyagPm2tWqxtby2/sAOBVQhonGnj2vB3rw42Vxkcdzdj485A39FLj8c1NtVcYdY8bOo8Ixi7bjanWCVgMDJGAIF+jM6CY+qI3WdKdPf7eAf9AsJcCgEIQOACBDTojd8lrx8m7WvzDZR39bQV0s3g+OVWTScE2dRgNLXPW65XXnfeq3h/VM/Oq3TG2uXz9YOrmY1FQlD2QrOrWyxyfy7PeztS32dPxF7BpnuQELSpE7aTDGf5NcLdrdAPGbmHC2893Ih5Ojvz6/juPASK/6w39K2OzWX1D+1Fdes8sJpYD29uzrlh+WxDAAIQgMCZCGgev1ad1ra3ll/YgcAqBGx8Xo/DFe9eNH6+qveR5iqD4+55Ar0X7r+eh80Zj64xpk4/ZFglNjAymwAC/Wxk0y5QYhoU54MV8p/OMVvTiuYsCEAAAhCAAAQgkJ/A4EQmf9GUAAEIQAACEMhBYO2599r2ctQZmxCAAAQgsD8BBPpMbWAdcSTEu/1jgnzquNnK5CtmIQABCEAAAhCAwGwCCPSzkXEBBCAAAQiUTWDtuffa9sqmh3cQgAAEIPAtAQT6b8l9uM464kigHxPnh46ZrQ9lchgCEIAABCAAAQhsRgCBfjPUFAQBCEAAAtsQWHvuvba9bShQCgQgAAEIbE0AgT4TcXXE7nNIeHf7pxyXrUyuYhYCEIAABCAAAQjMJ4BAP58ZV0AAAhCAQNEE1p57r22vaHg4BwEIQAACXxNAoP8a3fiF1hGzgn4cFEchAAEIQAACEIAABCAAAQhAAAIFELB5/Eq+rG1vJbcwAwEIQAAChRFAoM/UINYRRwK92z93Rb3ZyuQrZiEAAQhAAAIQgAAEIAABCEAAAlcnsPbce217V28f6g8BCEDgrAQQ6DO1rHXEkUA/Js4PHTNbmXzFLAQgAAEIQAACEIAABCAAAQhA4OoE1p57r23v6u1D/SEAAQiclQACfaaWVUfsPoeEd7d/ynHZyuQqZiEAAQhAAAIQgAAEIAABCEAAApcnsPbce217l28gAEAAAhA4KQEE+kwNax0xK+gzEcYsBCAAAQhAAAIQgAAEIAABCEBgPQI2j1/J5Nr2VnILMxCAAAQgUBgBBPpMDWIdcSTQu/1zV9SbrUy+YhYCEIAABCAAAQhAAAIQgAAEIHB1AmvPvde2d/X2of4QgAAEzkoAgT5Ty1pHHAn0Y+L80DGzlclXzEIAAhCAAAQgAAEIQAACEIAABK5OYO2599r2rt4+1B8CEIDAWQkg0GdqWXXE7nNIeHf7pxyXrUyuYhYCEIAABCAAAQhAAAIQgAAEIHB5AmvPvde2d/kGAgAEIACBkxJAoM/UsNYRs4I+E2HMQgACEIAABCAAAQhAAAIQgAAE1iNg8/iVTK5tbyW3MAMBCEAAAoURQKDP1CDWEUcCvds/d0W92crkK2YhAAEIQAACEIAABCAAAQhAAAJXJ7D23Htte1dvH+oPAQhA4KwEEOgztax1xJFAPybODx0zW5l8xSwEIAABCEAAAhCAAAQgAAEIQODqBNaee69t7+rtQ/0hAAEInJUAAn2mllVH7D6HhHe3f8px2crkKmYhAAEIQAACEIAABCAAAQhAAAKXJ7D23Htte5dvIABAAAIQOCkBBPpMDWsdMSvoMxHGLAQgAAEIQAACEIAABCAAAQhAYD0CNo9fyeTa9lZyCzMQgAAEIFAYAQT6TA1iHXEk0Lv9c1fUm61MvmIWAhCAAAQgAAEIQAACEIAABCBwdQJrz73Xtnf19qH+EIAABM5KAIE+U8taRxwJ9GPi/NAxs5XJV8xCAAIQgAAEIAABCEAAAhCAAASuTmDtuffa9q7ePtQfAhCAwFkJINBnall1xO5zSHh//Vm/g17n3n/cqlck6OuYt5PJV8xCAAIQgAAEIAABCEAAAhCAAASuTkDz77U4rG1vLb+wAwEIQAACZRFAoM/UHtYRR4K7xPrXz1qcv/+8Va9ft8qJ9U6gf/7TF/TNViZfMQsBCEAAAhCAAAQgAAEIQAACELg6gbXn3mvbu3r7UH8IQAACZyWAQJ+pZa0jjgR6t9+J9M8ft+r241a9B45LyHefssUnLIgBYoAYIAaIAWKAGCAGiAFigBggBogBYoAYIAaIAWKAGDhRDGTSpy9vVjdJKLSH216gv92q56/+ivnwPAT6E91sN+qi+4JPYoEYIAaIAWKAGCAGiAFigBggBogBYoAYIAaIAWKAGLhVrKDP9CghDK5YcPff/7lVD7eK3om2P27V48/+avpYnM/kKmYPQKATT//7f1XV/HP7te0++Q4P4oH7QzFAPiAfKBboH+gfyQf1mPsAQz5c3ICAux/CeyLcJl+SL3PEg7e5QWxTxPYEXNvSvttzp0QInJEAAn2mVrVEHb3CJhbr378Cod6tqOcd9Jla5NhmLZ4Q5v0DCT8I4kGFPZyBB0IsQiwPZhQD5APygWIBobEVGm0cdezhIN6vREDxQL4kX26RLxVvK4UvZgojQPsW1iC4A4EDE0Cgz9R4lqgjgd4PBKN9TrR3Qv3YNf66TL5itnwCig0fBwjTCNM8qOFBDX8x01n9iBDZCpESG+gvEJ4UC9wf9f3BWLr88e5WHmpcrXuEfEm+VCzkypfkn63u7u3LsXyyfdGUCAEInIwAAn2mBrVEnRDj41X0+v5wfx71s/9OerOVyVfMlk/AYgBhFmEWYRZhlldb2UO6XBPp3BN17PMXD4oB179r233yPQ8PG0eVP+TDww0IKB643/Lcb8pp8K35Kt42CG2K2IEA7bsDdIqEwEkJINBnalglaj8wiUX6f27V/Xar7j/rVfOv4DU3j+hHYzt2MvmK2fIJdOKAFfQmZvj7Cx7w4MGVjwHuB4QGiSIIvQjd5IN+PvBMyh/y4eEGBFwshPdIuE3+JH/miAdvc4PYpojtCbi2pX23506JEDgjAQT6TK1qiToW55vvr5+1SK/z3A/FPiNxXivrdU4mVzF7AAIWAwiRCJGssOxMqplIM5F2+RFhmhXpigHigftBsRD2DzaOOsCYDxfzE1A8kC/IF6l8oX1rxYfiLX9kU8IeBGjfPahTJgTOSQCBPlO7WqKOBHrf0Uf7JMS7z9Rxs5XJV8yWT0Ax4OODFeMmxsGDiZUmUaEQo33EB/GhWCA+eJBDPiAf+Bgof8iHhxsQcLEQ5oRwm/6C/iJHPHibG8Q2RWxPwLUt7bs9d0qEwBkJINBnalVL1CNifCjMj22brUy+YrZ8AhYDrKBnBT0r6DuTaibSTKT9pIgHlzy4pH+kfxzpH20cVf6QDw83IKB4oP/gwd0WD/IVbxuENkXsQID23QE6RULgpAQQ6DM1rBK1H/iNiPRTjstWJlcxewACigEfLwhRCFEIUQhRI0KUJpvkC4QHxQIPsniQRT5gheMBhrubuahxtXIk9wf9pWIhV3/pY2yzCKegLQlYPtmyUMqCAAROSQCBPlOzWqIeEefHVs2Hx8xWJl8xWz4BiwGEWYRZhFlW0PPOdXtIl2sinXuijn3ema8YcP27tt0n3/PwsHFU+UM+PNyAgOKB+y3P/aacBt+ar+Jtg9CmiB0I0L47QKdICJyUAAJ9poa1RB0J9H6gEu2Lxfjwu9s2W5l8xWz5BBQDPn5YQW9iBjyYWGkSiLCFsEc+IB+QD3jwoRhI5QO/r/whHx5uQMDFQhgj4TbjCcYTOeLB29wgtiliewKubWnf7blTIgTOSACBPlOrWqIeEeNjIX7ou9nK5CtmyydgMcAKelbQs8KyM6lmIs1E2k+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7s6qFezvGk4m2D0KaIHQjQvjtAp0gInJQAAn2mhlWi9gO/EZF+ynHZyuQqZg9AQDHg4wUhCiEKIQohakSI0mSTfIHwoFjIKTyoDOKNeFMslBpvPkYPMObDxfwEXCyEOSvcLjV+S7+/8G/8L5jIP/nv671KsHyylwOUCwEInIYAAn2mprREPSLOD62Yj/ebrUy+YrZ8ArDMTZMAACAASURBVBYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaOKn/Ih4cbEFA8XPV+uHo+2Lr+ircNQpsidiBA++4AnSIhcFICCPSZGtYSdSTQ+4FgtC8U5FPHzVYmXzFbPgHFgI8PVtCbGAcPhElNstwn8UA8EA8I0YoB8gH5QLGg/sHHRPlDPjzcgICLhTBHhNuKlzh++E7/ohj4Jl78NRvENkVsT8C1Le27PXdKhMAZCSDQZ2pVS9QjYnwozI9tm61MvmK2fAIWA6ygZwU9QnRnUs1EmgcTflLEg0seXNI/0j+O9I82jip/yIeHGxBQPNB/8CBPonvO8aTibYPQpogdCNC+O0CnSAiclAACfaaGVaL2A78RkX7KcdnK5CpmD0BAMeDjBSEKIQohCiFqRIjSZJN8gfCgWMgpPKgM4o14UyyUGm8+Rg8w5sPF/ARcLIQ5K9wuNX5Lv7/wb/wvDMg/+e/rvUqwfLKXA5QLAQichgACfaamtEQ9Is6PrZoPj5mtTL5itnwCFgMIswizCLOdSTUTaVbQu/yIMDAuDMAHPoqBq94vNo4qf8iHhxsQUDxc9X64ej7Yuv6Ktw1CmyJ2IED77gCdIiFwUgII9Jka1hJ1JND7gWC0Lxbjw+9u22xl8hWz5RNQDPj4YQW9iXHwQJjUJMt9Eg/EA/GAEK0YIB+QDxQL6h98TJQ/5MPDDQi4WAhzRLiteInjh+/0L4qBb+LFX7NBbFPE9gRc29K+23OnRAickQACfaZWtUQ9IsbHQvzQd7OVyVfMlk/AYoAV9KygR4juTKqZSPNgwk+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7kSXTPOZ5UvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfuA3ItJPOS5bmVzF7AEIKAZ8vCBEIUQhRCFEjQhRmmySLxAeFAs5hQeVQbwRb4qFUuPNx+gBxny4mJ+Ai4UwZ4XbpcZv6fcX/o3/hQH5J/99vVcJlk/2coByIQCB0xBAoM/UlJaoR8T5oRXz8X6zlclXzJZPwGIAYRZhFmG2M6lmIs0KepcfEQbGhQH4wEcxcNX7xcZR5Q/58HADAoqHq94PV88HW9df8bZBaFPEDgRo3x2gUyQETkoAgT5Tw1qijgR6PxCM9oWCfOq42crkK2bLJ6AY8PHBCnoT4+CBMKlJlvskHogH4gEhWjFAPiAfKBbUP/iYKH/Ih4cbEHCxEOaIcFvxEscP3+lfFAPfxIu/ZoPYpojtCbi2pX23506JEDgjAQT6TK1qiXpEjA+F+bFts5XJV8yWT8BigBX0rKBHiO5MqplI82DCT4p4cMmDS/pH+seR/tHGUeUP+fBwAwKKB/oPHuRJdM85nlS8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStR+4Dci0k85LluZXMXsAQgoBny8IEQhRCFEIUSNCFGabJIvEB4UCzmFB5VBvBFvioVS483H6AHGfLiYn4CLhTBnhdulxm/p9xf+jf+FAfkn/329VwmWT/ZygHIhAIHTEECgz9SUlqhHxPmxVfPhMbOVyVfMlk/AYgBhFmEWYbYzqWYizQp6lx8RBsaFAfjARzFw1fvFxlHlD/nwcAMCioer3g9Xzwdb11/xtkFoU8QOBGjfHaBTJAROSgCBPlPDWqKOBHo/EPy/W/X681bdm9Ub/twft+rxq1nNkbjGX5fJV8yWT0Dx5OOAFfQmxsEDYVKTLPdJPBAPxANCtGKAfEA+UCyof/AxUf6QDw83IOBiIcwR4bbiJY4fvtO/KAa+iRd/zQaxTRHbE3BtS/tuz50SIXBGAgj0mVrVEnUktruV8c8fdRK/OVH+Z/1PYv39560KV8+7bbOVyVfMlk/AYoAV9KygR4juTKqZSPNgwk+KeHDJg0v6R/rHkf7RxlHlD/nwcAMCigf6Dx7kSXTPOZ5UvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfuAXiPTvPxvBvRHiw+OP5unr859WpO/YyeQrZssn0IkDhCiEKIQohKgRIUqTTd+/kC/IF+QL8gX5gsUu5Q91N/VQ42r6y3pVPOOF/A8qPONNo5zCtiJg+WSrAikHAhA4LQEE+kxNa4k6EOfD1fOvaL87JvH+/mcr0LOCPlMDHcysxRNCC0ILQgsr6HnnuonuOVe8Idwg3BBf5/kLHRtHHWz8h7t5CCge3KdyPff7ee53tWkp7at4yxPNWN2bAO27dwtQPgTOQwCBPlNbWqKOhHi//8etekf7nRBfNe+gv0WvuTFbmXzFbPkEFAPuU4NOJhJMJIgH7gfyAe/EVQyQD8gHigXGB+nxgb9Hyh/y4eEGBFwshDkz3Ob+Sd8/5Jdl4w3yzwY39k5FWD7ZqXyKhQAEzkMAgT5TW1qijoR4/xobBPpM1M9r1uKJFfSsoGcFfWdSzUSaibSf9PIqH3t4Cw+EeoS0vpBm46jzDhWp2QwCigfyJflyi3ypeJsRopx6IAK074EaC1chUDgBBPpMDaRE7Qd+gUivH4jVK27C46lX3HTsZPIVs+UT6MQBQhRCFA9qeFDDgxoe1PAXVdYX8KCOB3V+PP1hfOTPKX/Ih4cbENC4WuLslPjRueQb8s038UL+2eDG3qkIyyc7lU+xEIDAeQgg0GdqS0vUgTjvXmPz+ln/SWX8nvnqn1uV+pFY3kGfqYEOZtbiCWEWYRZhFmEWYRZh9oMQiZDUX0EtJl4kgZ/dQ1fhYeOog43/cDcPAcXDVeKf/Ff3CXu1t+ItTzRjdW8CtO/eLUD5EDgPAQT6TG1piToS6N1+CfG3H7fq8bP+p/Pdp38ffXCdjmVyFbMHIKAY8PGBsHA5YYGJ1b4TK/jD38UA+ZdXISgXEA/HvB/8PXyAMR8u5iegcbXuafI7+V2xkCu/k3/y39d7lWD5ZC8HKBcCEDgNAQT6TE1piToQ2kPh/fnzVt2bHyhy595/3Krnr744zwr6TA10MLMWT6ygZwU9QiFCKSvo7SFdrol07ok69lnhrhhw/bu23Sff8/CwcdTBxn+4m4eA4oH7Lc/9ppwG35qv4i1PNGN1bwK0794tQPkQOA8BBPpMbalE7QcmAyK9xPdQuI+3O3Yy+YrZ8gl04oAV9CZm+PsLHvDgwZWPAe4HhAaJIgi9CN3kg34+8EzKH/Lh4QYEXCyE90i4Tf4kf+aIB29zg9imiO0JuLalfbfnTokQOCMBBPpMrWqJekScj8X4oe9mK5OvmC2fgMUAQiRCJCssO5NqJtJMpP2kiAd1PKijf6R/HOkfbRxV/pAPDzcgoHig/+g/yOJB7/p/4aV42yC0KWIHArTvDtApEgInJYBAn6lhLVFHAr0fCEb7QmE+ddxsZfIVs+UTUAz4+ECIQohCiEKIGhGiNLkmXyA8KBZ4kMWDLPIBKxzLH+1u56HG1cqR3B/0l4qFXP2lj7HtQpySNiRg+WTDMikKAhA4JwEE+kztaol6RIwPhfmxbbOVyVfMlk/AYgBhFmEWYZYV9Lyz2h7S5ZpI556oY3/9FYpi6vpLbbtPvsNDceBjofwhHx5uQEDjavID+WGL/kLxtkFoU8QOBGjfHaBTJAROSgCBPlPDKlH7gd+ISD/luGxlchWzByCgGPDxwgp6E1/gwcRqi4mVyiDeiDfFgvskHogH4uFYD1r8PXuAMR8u5ifgYiHM4eE2+Z3+LUc8eJv5Q5sSdiDg2pb23QE8RULghAQQ6DM1qiXqEXF+bNV8eMxsZfIVs+UTsBhgBT0r6BEGO5NqJtJMpP2kiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+BB6xYPWhVvG4Q2RexAgPbdATpFQuCkBBDoMzWsJepIoPcDwWhfLMaH39222crkK2bLJ6AY8PGDEIUQhRCFEDUiRGmySb5AeFAs8CCLB1nkA1Y4lj/a3c5DjauVI7k/6C8VC7n6Sx9j24U4JW1IwPLJhmVSFAQgcE4CCPSZ2tUS9YgYHwvxQ9/NViZfMVs+AYsBhFmEWYRZVtDzjm17SJdrIp17oo79Y70ahfY6fnvZOKr8IR8ebkBA8eA+ub+Pf3+rDUttT8XbBqFNETsQoH13gE6REDgpAQT6TA2rRO0HCiMi/ZTjspXJVcwegIBiwMcLK+htMgUPJpaalLlP4oF4IB4QWhQD5APygWJB/YOPiQOM+XAxPwEXC2GOCLcVL3H88J3+RTHwTbz4a/KHNiXsQMC1Le27A3iKhMAJCSDQZ2pUS9Qj4vzQivl4v9nK5CtmyydgMcAKelbQI0R3JtVMpHkw4SdFPLjkwSX9I/3jSP9o46jyh3x4uAEBxQP9Bw/yJLrnHE8q3jYIbYrYgQDtuwN0ioTASQkg0GdqWEvUkUDvB4LRvlCQTx03W5l8xWz5BBQDPj4QohCiEKIQokaEKE02yRcID4qFnMKDyiDeiDfFQqnx5mO0/CEfHm5AwMVCmLPC7VLjt/T7C//G/8KA/LPBjb1TEZZPdiqfYiEAgfMQQKDP1JaWqEfE+FCYH9s2W5l8xWz5BCwGEGYRZhFmO5NqJtKsoHf5EWFgXBiAD3wUA1e9X2wcVf6QDw83IKB4uOr9cPV8sHX9FW8bhDZF7ECA9t0BOkVC4KQEEOgzNawStR/4jYj0U47LViZXMXsAAooBHy+soDcxDh4Ik5pkuU/igXggHhCiFQPkA/KBYkH9g4+JA4z5cDE/ARcLYY4ItxUvcfzwnf5FMfBNvPhr8oc2JexAwLUt7bsDeIqEwAkJINBnalRL1CPi/Niq+fCY2crkK2bLJ2AxwAp6VtAjRHcm1UykeTDhJ0U8uOTBJf0j/eNI/2jjqPKHfHi4AQHFA/0HD/IkuuccTyreNghtitiBAO27A3SKhMBJCSDQZ2pYS9SRQO8HguG+X/UT1/uft8qJ8r3jzT6/P5OvmC2fgOLJxwFCFEIUQhRC1IgQpckm+QLhQbGQU3hQGcQb8aZYKDXefIyWP+TDww0IuFgIc1a4XWr8ln5/4d/4XxiQfza4sXcqwvLJTuVTLAQgcB4CCPSZ2tISdSjGp7YjgT5cOa9ts5XJV8yWT8BiAGEWYRZhtjOpZiLNCnqXHxEGxoUB+MBHMXDV+8XGUeUP+fBwAwKKh6veD1fPB1vXX/G2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuBX0qYb/bpPK2glyivTx33djL5itnyCXTigBX0Jsb5+wIe8ODBFQ+ueHDFgyse1Fhf4MQn+sf+gzvG0uWPd7fyUOPqrYVayqsfll4xP5F/trq7ty/H8sn2RVMiBCBwMgII9Jka1BL1iDjvRXhW0GdqgXOZtXhCiESIRHhBeEKIRIjkwaTFgBc94AGPD+MjG0eda3hIbb4koHggf/QfZOkhAg/61nvQqXj7Mly5rHACtG/hDYR7EDgQAQT6TI1liToS6P1AMNwXCfS947yDPlMLHcus4snHB0IEQsQHIUKTK+KFiadigYn2ehNtMeX+4v5SLHB/HeP+8vdsacO/16O63e7V812aY+f2x8VCmMPDbe7nY9zPR8u/Reafc9/mm9XO8slmJVIQBCBwVgII9Jla1hJ1KMantiOBXq+2CT/NViZfMVs+AYsBhFkvzjseRxuY4y/vgFYMEL/cv4oF90k8EA/EQ/7+wcZRQ0M+L5TXoq0/9/6sNtHMEeiHWiTrfsUD+Zf8u0X+VbxlDWqM70aA9t0NPQVD4HQEEOgzNakStR/4pYT5Zp/O4x30mRriJGYVJz6eWEFv4jw8mFhtMbFSGcQb8aZYcJ/EA/FAPOQX1sV4jfvN20iMC9/Pu7+fH6/2oN8X7mgPrbuFQL8uz4nWXCyEMRVuk9/p33LEg7c5MT457VgEXNvSvsdqM7yFQKkEEOgztYwl6hFxnnfQZ4J/QrMWT6ygZwU9wmBnUs1Emom0nxTx4JIHl/SP9I8j/aONo3pjxFf1cOLKVivm4/IR6GMiC7837fnh4Yrigf6DB616CJhzPKl4WxjcXF4oAdq30IbBLQgckAACfaZGs0QdCfR+IBjui15x0zvOO+gztdCxzCqefHwgRCFEIUQhRI0IUZpski8QHhQLOYUHlUG8EW+KhVLjzcdob/g3TdDtXbbWDgT6tUg2dqa1p4uFMGeF26XGb+n3F/6N/0VROv+sHP6Y24WA5ZNdSqdQCEDgTAQQ6DO1piXqUIxPbUcCffjueW2brUy+YrZ8AhYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaO6g353tXzXou1HxZdV1XVnit7t9ujCt6M463Xr8xJ/PCrF+NvVaecQKB/PWo/ZLtznvxubOgc99k/L/Yz9vHTcVdYI3Q3QnaqnLqeznZkTw69n9V95Pq6Sp/LqXyd6zp0GXUZ61VFIZuhH+ANz9G94T7dfr6TLxUDa8WD4k23MZ/nIkD7nqs9qQ0E9iSAQJ+JvhK179hTwnyzT+fxDvpMDXESs4oTH0+soLfJEzyYSGoSxcQaYYF8QD4gHyCsKQZS+cDvS40LO0JyLGbrgkZIjl6FUwvGKaG4u89bGRToa2H+/mx/llZCtLRud70XoCeU768Nz3P1C75/Ol6JR1h443voYyiI26k67+7e69+yTHGaWk4t0MeM9FCgLaNuKVbQMx4qczw0mH+UYvg8LAHXtrTvYZsPxyFQFAEE+kzNYYl6RJznHfSZ4J/QrMUTK+hZQc8KL1a4scLPHtIhRJQpREgkpX1oHy9aFLCwwMZRg2NECb7NKvZA0HaX1AJzLAb7I7132NfC9TyBPhS+axfTDwR67jdienv9J4H60/HhusbCvgR6E+e9c+IYser5Ob0cCfTdcnyj+PFAd//n+jk3FQ+lxKdyJv6c80Gz4q13/7LjFARo31M0I5WAQBEEEOgzNYMl6kig9wOvcF/0ipvecd5Bn6mFjmVW8eTjo4CJLhOJepUi7XHOiRTxTXwjLCMsk9/Pl999m34c/klgDn84dlz0jcX7+QJ9QswffSgQVGJQ+L5Vt65ybRfV/g4dH65rXa9WeE/Xs+EXPeDQK3OmPEiIy6kF+gSjRN1VzlDdBcHFQniPh9vkf/J/jnjwNhWAfJ6KgGtb2vdUTUplILAbAQT6TOgtUYdifGo7Euj13vnw02xl8hWz5ROwGGAFPSvoWUHfmVQzkWYi7SdFPLi0vyqAx/mEZT00JN99n+9sHDVxyCcRu9a4h0VrZ25Lgb4Wr5tV/sH73Vvhu65g97xWVFf1h483dQ1si1392dqqbcTC+UyBfkI5OQV68iX5cov8qntI9x+f5yJA+56rPakNBPYkgECfib4StR/4pYT5Zp/O4x30mRriJGYVJz6eEKIQonhQw4MaHtTwoIZXHVlfgHD9vXAtceoK4wtfx6njws774ssQ6OsHAZEgnlxFHlSyOR6+Dz446l5s3/yQq4T38bqG164i0A+s8g/LySnQXyn+VVfy5T75clb+6dwAfCmdgGtb2rf0VsI/CByDAAJ9pnayRD0izoer5Me2zVYmXzFbPgGLAYRZhFmEWYRZhFmEWR7UWgz4STE84PFhfGTjqIlDvlh8jlfJt2YSgnZH3G/P1Kr1jiatH1UNfiC2viK2G39v7H4S6PXjsrdI2G/dqn981o4PrYAPLrCi3Q/BxnaHrq/9b1f6D53XLyenQE/+YAX9Fg8u5uafxF2w7a7BvLStG0cp7XDtexSw+AmBCxJAoM/U6JaoI4HeDwSjfaE4nzputjL5itnyCSgGfHwgRCBEfBAiNNkgXph4KhZYMbfPijn4179nQPwRfyX0R96HeMjnhSitHm8ONuJU5z3mWmneUdcbkfkWXV81YnrwHnaJ886HjgmVdbtVrXit1+aE4neqrKac8FrvZ+hPdN2n4w5Bsq5u973zXvv4IUZNb0h4jwX66eXME+iHyu82vGuHMCbDbfIV+SpHPHib3TBMf3u/qsfdPfxqXmV1v1eP1zt9bq69CPSzyKqtZl3EyRCAAAQSBBDoE1DW2GWJekSMD4X5sW2ztYZja9nwHXc4cVjLMHZSBCwGEGa9OO94IHwhfCkGiAfuB8UCwgrCCvmAfJDKBzaOSg2yApFc54VieXtJK4jrvFsgwrfnBeKzRDanyjfCd1+gd4K6hHS9Xz41xk6dU+8L/Q0fBtR+hoJ9I7TLL//ZPV7XI1HXjuOyE/s5JJAnBHpf0Ody5gn0MfvYv7p21n6MJxlPb7DwSfHWyRGpL69H88qpW3V/PKrHI/je+yublIGV9iHQzwI5uX1nWeVkCEDgigQQ6DO1uhK1+/wkvn86LltJV+NJxdBEIXnxgp0I9Avgzb9UMeDjaYOBpCa3lIfQoVhA+ET4JB+QD8gHPBhVDBwxH3if5w/BuOKEBFwshDEcbjPeYbyTIx68zQ/3UvJ3Jvwzp3vnL2w+mFl+GIF+FkPXtlPad5ZRToYABC5JAIE+U7Nbos64gl4rZMIFLfGfn2aqnvvb28R7J7OVdnnDFk+soGcFPe+g70yqmUgzkfaTIh5c2ipIePAgRSI6+bHNjzaOuvyIEgCOgOKBfEm+3CJfKt7G7z79hUzqL1rGr1z9KAL9LKTT2neWSU6GAAQuSgCBPlPDW6KOBHo/EIz2hSvoU8fNVsfX5k9Ct1ox3ym7QqCPeSz+3rRn+LQlsKkY8PGBEIUQxYMaHtTwoIYHNbyawfoChOhWiJbYxHihLzx6JsHYis3rEtC4mvul/qsg8kU/Xyg21upfPucfCfTR71QM3qbv6vVsX4HjY3roffWN4N6fZqrM6KFAINC/3Wt37u2rt+4P90Ku+L931T3PnX+vHsnX8vT9vt+f1atjcso57oJ39Xrc7bVAjsH9/qh6r+wP6u/9tFd8Be/3fz+rR1DPtO8dJ+2LZ+/GZPwHAQhAYCEBMslCgEOXW6IeEeNDYX5s22x1ChsXdDun5vjiO7r0ex1zFHd+m+PtaTGAMIswizCLMIswizDLg1qLAdc/ri2kYO98r/KxcdT5B5TUcAIBxQP5g/y5Rb5XvH0MzUZIduenhXBZkLB+q25OlPfvq2+Fandt579AoO7st9++SAv08tuJ3uH78Ds/oN28gsf7fH9Uz9erer1asTv8fQxXdv0aH1e/Z/Vy57qHDPeupjDlHCfOP72gfu/a8uJ71179l/81q5qtq0/7Q7x3bUf1jH3vsmu/iVO7hy0IQAAC3xFAoP+O28erlKjd5yfx/dNx2eoWqk5pylP29lzZut2ijtg616hDc4WmOvVAoFcnKtvxmMD7HQw4hs+L/Yx9/HTcO1s97Kl4/bQ/9qd+NZCzHdnTic2PeA37Oa2cmltdhy6jLmO9qkjl1Z/dc8JjWwwkVYYrV9vuk+/wIB7OJ1ypTbm/ub8VC+R7+rsz5gNfJz8o5X9XJ+BiIYzxcJv8R/7LEQ/e5oQbr7vCuxGyoyXrNnfU3NXsNgu+bt15ZHIu76/RXDiac9u8PbJTDdh/v6p35GOlczt/7d+U19lnzjcbU87Rj1QndBDN40M2A/Uxju6BSLjaXzZG/Wz9dm07tX3bq9iCAAQg0CeAQN9nssoeS9TZVtB7RT34k66oY7VaNB1p1MHUgnG30607qe4+b6bp1MJ+Th29q2fYoUmIDs/1dieU768Nz3OdY/D90/FKnWlYeON76GPYGdupOu/unqa3LFOcppaTZjQwENIgxhyyBvQbFk+soPcPDPwgiBWk9vAEHgirCKs8OFEMkA/IB4oFhMZWaLRxVHd4xbeLElA8kC/Jl1vkS8Xb9NstfsWLexWLrh6aS9bHNc8N576ak7Y2PtjSvDgUrZtLkvZlrvOZ8lP77tWz9x4aXTzjHP86m3f1fof/XvWragINQfXvMHHFpbQD74Z8aDUBeZf6nN++KSvsgwAEIFBVCPSZosASdSTQ+4FgtC9cQZ86braSvqoDqZ/c3sLOyP6MLNW59IX7usOdJ9D3OjoJzZEfPdebDrG9vvGnP3JoLv10XH8y169rLOxrYNEtShyj63t+Ti9Hg4FuOQN/kSBuvZPr6isGfHwgTCNM86CGBzX8RUtn9SNCZCtESmygv0B4Uixwf9T3h78negNSdlyRgMbVukfIl+RLxUKufPld/nFCvV7Fojlqfw7fuYcbcb3zGppmX3+aOTD/HRHoNb9t5/Aq3b2H/lk9/et2wlfiyO/mvPBd7+71PM/EO+0/ntMwiP5qXve1/wy1iMH6DOkLA1xU1ehT5Ua7+QoBCEBgNgEE+tnIpl1giXpEjA+F+bFtszVatDoS9361Z/PjLUOdTm2oXh3edprzBfqEmD/6UCCowKDwfas6A4rgktrfoePDda3r9ameDT9jp4Jru+0gZHo59QAmwShRd/szwP7IyTtiMYAwizCLMIswy6un7CFdrol07ok69vmLB8WA69+17T75noeHjaM0vOPz0gQUD9xvee435TT41nwVb9/edJoD19PEZi7am7M21vcQ6N0PyQ6K5e0cPKy/E/PDH2VNLNb3gn/6nJbBq7N6PlhJHxaGQB/SYBsCECiYAAJ9psZRR+wHJiMi/ZTjsjXF1WQHPiD6binQa9W66qLPVviua9c9r9+hDx9vOuoJg4PaRiyczxToJ5STQ6D38cIKehMz4MHESpNAhC2EPfIB+YB8wIMPxUAqH/h9UwbTnHN6Ai4WwhgJtxlPMJ7IEQ/e5pd3Vnd+r0V5/XmyM6+5cmeOPShQD9gaPL+138oLsuFewxO+iF77034KhXvnvmMztEDP16l3zjTbKmN41f/Qwrt59r3/7mE7/0EAAhBYSIBMshDg0OWWqEfE+bFV8+ExszVUWLi/6cA6T9jbHjQ8s/kV9bbTTAvXA69k8eXEIndtPhb+6+/RuclV5IF7zfHwffDB0fadcfa++KEOtnOV/5KuZ9MR91Yj1HbbQc70cnII9GMTTx1jYsHEwuUM4gGhSjFAPHA/KBboH+gfrpoPZo2l+0NH/qV0WQAAIABJREFU9pyMgOLhqveD+gTqv834QPE2ehu5ua9/p3p01ruZe9qcV69b7f4OnL/Kzo3m3T2Buy5DYn5vvq3z4x+b1StZO/sb/1Jz6Lt7ENZqDVHNmq9T5tb9c+R7O0cPrPtV9cH3pj79c/t266sQ6AN6bEIAAhsSQKDPBNs64kig9wOhaF8sxoff3bbZmuBrLD7HYnlrItEhNZ1XrOerA+zsn9zRJcpxTnwS6G0FQDTAaCvQrBDQ8SGBPbig2YwZ1buHrq/9bzv0ofP65eQQ6H38sILexGd4bDOxYCJXi/1njLfXH66P+Vf1/Bvh8oztq3sXYZ74Jr6bFdOJ4Rq7rkfA3Q/hPRFunzVfqq8/a/1K7+98jI3darY4zb2utn6H++Oh98/HYnwzv3Zx7N7j7t/7PnSuK1SCc2v77sXze1V/RiK6n+fr2M0/OHBl6DU27by4rpBW+N8fz+r1elXPZ3tuR6D3dbxXOu8VvObGdIYp5/hiWwbO3vP1qpy9Z8Os4+Nk3UINJF4RFx2OPi2fRPv5CgEIQGAuAQT6ucQmnm+JekSMj4X4oe9mKyzbdzRRp9F0Pp0/EVNnb72eMzLU6TQdXfAEXOK886FjQmXdugOG/mr5VFlBh6oXznk/w/pE13067qv1rAcOHUebP8UL9i0T6NuHCx3OeqAQlDNPoG/qG7APm9tigHfQe3He8Sh9II5/rGBXDBQbr3//2yZb8tV9Fusv+Y/8R3xyf37Z/9s4KhxcsX1ZAoqHS/R36uv/+C/548v8oTHSt/GiePt4w71fXmCWEO6uq1fVh6+OkZV38txn5zUzOtdNVF/V8x6I+M1q/eRiPj/PrxfBvTtiu/tR12FfVM/brX7dTd/2u3o97jb29OffH1XX5ynnqF4Tz210i45o7000mkQ4f/f7Ix1CxQ18qt4Dh9kNAQhAYDIBBPrJqOadqETtPoeEd62O/3RctnoeBCK5zul3PO6qVhDXee0PyUZWJeg3K0u8CN3s6/RdvmwnqKsD00p/rWgP7abOqfeF/oYPA2o/Q8G+feed1SH5J3OJunYcl53Yz8bHnkBe2wv9rGv2uZx5An0g/Hv2Xf/aOiNMa5CMkIiQ6u6LS8aDJtuD9f9v9Why+PvDX9zcbr9Xry+E7/d//uUn+vf//LI2uGx7fMGP/EX+4n7ZPn975uHwlO3LEnCxEN6D4XYx+Vl9/aCw3vT1v/27U5fY//ov5W7W18fHx76rry+Sz4fxjauX/pXgv/fhsnfcuSvu2pb2PXcbUzsIbEUAgT4TaUvUuVbQZ/Ibs2USsHhCCGIFKStIRyeiYxPNkiZq8uVbf/3qqj/+O3g/eIH+t39XTqD3k4Z4otpM/B9/DRyPz4++a9LuBPqk/ej8pfXl+rKEBtqD9lAMHOX+t3FUmcO8w3ilxTT9hSuHqYJ3VPFQdPz+XQvvt6avd/dc1996Rfyt6ev7x+vz3XjB9fVDx3UvDx13ZephfLf82B++D/Fx+/2xY90meDuRAO07ERSnQQACHwkg0H9E9N0Jlqgjgd53ztG+cAV96rjZ+s4VrjoBAcWAjw+Er6JWxHya2HAcIUsxsNr9q1V1K6ygl2/uczX/mhyFve1XCNOe5BvFAPdf//7zTE4wJtyzCmcT6Iu+X9TXL1xBT/9exviG/LNn5spbtmtb2jcvY6xD4CoEEOgztbQl6hExPhTmx7bNViZfMVs+AYsBhK+vVwBpEsZEpYyJCu2xTEhcvIKeB3086KM/oT+50IM5G0eVP+SLPGxeqRi9rjE6ia8zCSge3Gex45GVVtAXWz/yz8yo5fRSCSiflOoffkEAAschgECfqa2UqP3ALyHSv3/dqvuP+mmrzn382X9fvY55O5l8xWz5BDpxgLBmkyl/X8ADHlcTGrWqblBYGHsH/a/q9ce/Oj/Qdf/t9+r1d/Tg5q/f/Wog92fx7nzloGfzZ/JVc1x/9q4HX6///B7Z/re997a+X39VQ+d07+f61TnhD6W544+/Eu+8b3xxx99/dct/8I588sPV8gP19THfzSd1fvP7yh/yRR4i0EdAVvnqYiGMkXBb/dnuwrb6+i9X0A/19Z36Bf1n29fXfb6vf3C85ZHun/V7NrI/1NfreG2vHhOoPfznb0H5YT5rfNGr+drxwcD5zbXd8r5/1U/t7/fX+xhbJXoxUhoBxW9pfuEPBCBwPAII9JnazBJ1Spz/sx4UOoH++etWvX7dqkcj1t9HRPpMrmL2AAQsnsKBamEDz6UDV65ftqIaftfi990K+l/V87em//nj39Xrr/96sbzOL/+qnn8HE89gUu6O3//4vXr89q/KCfTueyjQ++//c0J++9BZtu/RRFvn3KPyVbaLY2dPft6a6x/RQ4U43t01Otdtfzo/vp7v17p/aO/rtbfPES53bfZfI6w3QrDPS6+g8Pezfph5f1bvzu57dbvdq+e7qvQ6Gflef9bH2ks+lONOfD2q2+1RueJfjzZPq5zWltt6V897eE59nZ3jbd2q/oL++DpnI7p2ti9W6uobIdNi88HXK+jV19fCtfXHTSzG/W3Loj5ffb3jomN6GO++h/24/+4ezLvxQfCgX+f4481YIx4PVP+rhX5fxm//qh5/1AsDJLzf4wcTGpc04wK3uMBda+cX/Js4vo6b5p/VbxkMjhCgfUfgcAgCEJhFYMuR6izHjn6yJepIoHf7q39u1fuf/mp5/6N+bgVg4hp/3dGh4P/XBBRPPg4Q5lkRyoOawRWSxU601/xTbq2q80L0735Sq4mt+wzFafcjsWKiPNL7sbjAns6VAH+7RcK97DUTZU3abaL94cfqvPA+9uO1//t/lX6ANpXv6n6yKwS0vt7sIYOEBT9x/1Ce6pwqT8dkj+/deIIHPBQDR7h/vI9fj8RmXCjxPVSxG2E7/HFVCfB2WnNdeE5Vjaygn1hOLdDXontrW4J6V0T3An740MCVEX5PCvSNj+F59jAgeqDQXO/a4pMvM4jPPtWVH8ZsuF1MvlffbA+q4/6++Wu43+ofk9W9qD5Ufb3VR/ZC4Vuit3sw3jykt/Ndfx8cr+1L/L/5H6FXmV1+jfD+YTwgP92P4Havb378Nh5/mC/Rink9yPhQnnzt1G/D8bSv4+xI5YIjEHBtS/seoaXwEQLlE0Cgz9RGlqgjsX3sXfPPZhX9K7rGbGXyFbPlE7AY2HAgufdAlvIRfhQDftArYXhNofvA95NWjCk3JD87wnQzqW5WnL3//lXpn7v24VbWh+cHAnySf++4Ju3RxLnTXjrnVj1Tr6rx7aEVdb9Hr8ap7wdN6NsHA+kVfnXstOXFf3qv2HKfyfoRb50HO/AiHysGjnq/OL+97xsM+epV6l3h2xXbE79ttbo7txHMI5F7TKCfXE5SVNfK+nA1/MjDAHFL2Bryw3wP65S43pse2q9yV/5UPBQdzxKem9gNfe5sR8J0/SDcvbqu7k/V17//boTv6HxnS31qikd8vP4LN/cXdbV95Ya2P1XfO208kOqf1dd3/AnGHSqzPq7y6hX1Otb6s3/+dn56X1eOY8yVQYD2LaMd8AICZyCAQJ+pFZWofWccCe4S6d176N3xx8/6nwSXUKDv2MnkK2bLJ9CJA4QjhKMDC8slTpzkk8/XR7i/tArO/UVW0t/UO+i1Iq3ud8KcEm7bivvBiXAz0R047oV+NxFtVvyZPQnhf/+7fhjQTFYf//mvrcKr+Te+RysCbaLdlNtZcad9CR61kFCL/YdpX+5vH9e019D9Xd+D8JnPxzPLPuQbFrnrFfORcK9V8D4nRqvNva9D9ob269U4QTle/E7YTqzYr8X2W3WzZf0RsJ6QPuyHu7In3s/wJSp51a8uFsJ7KNy2/ibZv254/6mv760w14PlVH/Z9v+qY+8z7F9H+k8/vkgdDx8cuFfT/CdeAV/792k84P8iLlwYEPH2fv/x37Y/aHxxDxO67TX+YL+U9vQ+rxrFGCuFgO6xUvzBDwhA4LgEEOgztZ0l6pQ4734gthkY6rzwMxTonZivY5lcxewBCFgMINy0A/VoIO8nEvCBj4Tgk8eH70PCiWtU3/7EtzuRb1fUBSvswvtncCLcCAMfjtvE/JZeQff+qyvUt39an17hZ/e3xIKm7pp4uxzZXwGoVXU3W42v883eReKF+u6/glJt4GJV2+6T79vwsHFU9jFfI1gPjvMD4bzxZVwUHxLAZ5QzUxTXq3dqZpG/JxPoi77/JIRH/V2bP9L9pfr//gr6pr+PxguOQb//bB9EDB13/XgdI26uGr16LhhPpMcD7YOE3oN8d636+jBfBuMOMajbT309K+izpzcKSBLQfZA8yE4IQAACMwgg0M+ANedUS9SRQO/261U2j1/d99BrPwL9HNLXOFfx5D41KGVij7BBPFz0ftCqusF8kJr4zlxhNjgRboTOT8cb4dHnrpEHCW9Nwm2F4PhEW3/23llBJxsJHqygR5hWn0m+vGi+DIRCHwPZh41DgvpAwY3gfb+7H4cNXzej84fsDe3XdcHnTIHerrTV/YFIfzKBvuj8oL7e+sc4n3cfvNd1UR868cH0SP/p7X067n43RucMPkiox+vxeOBT/+zO7zw4aMrp9P/+/p45vtnpweg2+cfuXjY2JOBj241B+Q8CEIDAQgJkkoUAhy63RB0J9G5FvF/Z8KP/Y7AP3kE/hPPy+y2egommJhXu0w/6mmN8hwfxcH4hav4K+vEfX638O+nbFXNavdafCDf31+BEObz/2gcFw/mqWQEYTexdDHcm5i6//d3aa1fc1+Ulz//fTKGC/Mpf4NCfnnY84XKE7xuzjyiH3iWfKrgR2f072tM/2mrvce+9cmZGOd8K9JVelxO8Hqcn0CdeY2NVTTxEWOCLmV1hQ/HgY6LU8fOXK+iTD7KD/u0d/RisY9Drb4PzPx2v/tf0zYMPEtzYou2/NR54/VHfkyrb5i/W10d/gReMO2Sjbj/19aygX+HWwMQXBFwc+lj84lougQAEIBASQKAPaay4rUTtk3Uk0r9+NgOS5vP5Z/eVN+EK+o6dFf3D1LEIdOKg1IkEwsZphY3uRChewcX3zfloVV1ixXjtSzsRjv903D8gdpPxP+o/TX/99e/q+Uc9Cfb9lfLL4ES4ae/4eCMkOLuvv/5bObvKW4+/6mvc9/vtX75sd477rj99d+e05bf+u3fZP/74vXoEPmoyb+c3vtj3QFj4tEJPbec+U9dznPtbMUB8HP/Bp2/DLYZ/Wnkeier+1THBvvrVNoH4nbxuRIhPnt+I6kE51VRR3NsLVsvrh2tvwb6EQF8l/Rh44DDVl8zt5GIhvKfD7WL6A/X1g8J301eG75T3/V/z4Lvp659Nf6u+3vWhVt+R/tPnvvi496keM6ivD/txf83E8UAo2jt/hvp6a49g3GH++/qygj7z7YL5DwRcPPqY/HAehyEAAQh8IoBA/4nQl8ctUUfivH4g9tmI8zrPve5Gwn0o0PMO+i8b4GSXKU78wBchqZ1YBEKc2NhAvjnGd4RHP2g+WTx8s4K+vkfqiWz8OyjPv37Z67M8r8GJcBNPveO/qtcf/+r+vspvv1fObsu/Pkf5zH/+NrTi7Zd/cBD6ee/Za4V/Z6sn3LOCnhXx9JfB/dfeL1fsL5V3thseNqvHG+HGl98TzW/V/fnuuKT3v4enmgDubQWCvr/yQznunBmiuMoXr1sozputkVfxhPX1fxnQqd4sX6IrV/3a1q/gB09frqBXX+/65LCet4H+1p3T7z/bfBEfH+rr2/H2lPFAa989OEj19a29+tzwL/uUw5xvlfX1Q+OJ5vod+wO1w6pBjLFiCNC+xTQFjkDg8AQQ6DM1oSXqSKD3A4lon0R7ifHhd+3z12Xy9QpmNeGIJ0JHqbviycfByYRGDbJ7A/EdB9LyCd4FT1yJD4S3wb8gaCf+upfJLzyoI5+Tz30MHGXgh59ZCbhYCHNCuE1/QX+RIx68zaxRjfG9CLi2pX33ok+5EDgXAQT6TO1piXpEjI+F+KHvZiuTr1cwexaBXmKTHwQg1HdX/MIDHk0McH8gxClXIrQgtJAPyAfKAz4WrjDopY4fCbhY0D/6i/1XmKsNzpqvLdY+RiYnHHHOTvsStxCAwFoEEOjXIhnZUaL2A40RkX7KcdmKiij8a+KHoQr3uGT3FAM+XhCiEaIRonl1B39B0Fn9KAFOk3y+I8zTXyLMx/nAx0TJgz1824yAxtWKEfIF+UKxkGv8UEb+aebnqddPbXb3jReEQD/Oh6MQgMC5CSDQZ2pfG/iNiPNDK+bj/WYrk695zCLQr8nVYgBhFmEWYRZhlle72EO6XBPp3BN17LNiUzHgRRsevNs9nYuHjaPWHJxh67AEFA+54o37m1fNuRhQfCne9r9hyhfo92c034Ny2ne+71wBAQiURQCBPlN7WKKOBHrfUUf7QkE+ddxsZfK1a7bpuIM//Uz+UFX05L1+2l3/cJWefMvv+vPzj1p1ynFO+R+1elQvv9n+KertFttyJ7+r5z08p77O6uZtpX7UKr7O2Yiune2LlbraRshSg/5w4Kd97jxtc7wdGIsJfIgPxQL3B/cH+YB8QD641oMSf8+vNjLD0JEJuFgI+4Bwm/EB44Mc8eBt7n7TINDnaALXtmW0b47aYRMCENiSAAJ9JtqWqEfE+FCYH9s2W5l8NbPvZ3V3HUyolDfCdvjjqhLg7bTmuvCcqhpZQT+xnFqgrzu81rYE9a6I/nrcqlv40MCVEX5PCvTpQYq3FT8EaK53bfHJF+O54obFACvoWUEfrMiRuOTiQ9tMLJlYEg/cD+SDawnPtPfn9rZx1IpjM0wdl4Digf6S/nKL/Kl4m37HvKvX417Pyxvx935/VK93ZCGY375fj+D8e/V4dk+u57f1vFr++E+b0Ee23dcx+3Lm/awetkiuX25t9V15/+w858fAuU2Z7XzbWXhXr2dYv5uf57tFfN3/+ufd7vfqIV/Dk8fqFrELL0tti2fqGPsgAAEIzCGAQD+H1oxzlajd5yfx/dNx2ZpR/Fen1h13V/h2hnrit61Wd+c2gnkohvvShwX6yeUEHWenQr39w2XZdb1rmnqlVsvr4UJYp8T1dTUf/on52NjGfFiwoRjw8cSfwpsYDQ8mVltMrFQG8Ua8KRbcJ/FAPBAPn4VxMSrhfvE+LBiLcel5CLhYCGMy3Ca/07/liAdvc9ItpMVo9+r+eFav1ysQp6O/Im/mp06EdvadiP8IhP2OyP1+Va9Xsxjv/qiezq7719Xxux7G9h+1fVeWL+9Rl3vz5bYCeqdcJ68/W//qcltRPz5XDwXC/Xq40OFxj1hIk3C+OVG+8dUvPnRs4sl6XLcxdl0qvW/i0TvADghAAAIzCSDQzwQ29XRL1IdZQT8sctedaiTcaxW876DjDtJRGrI3tF+dd1CO7zgTthMr9tVxd1b/h43VdMJt3zzsh/fercgPxfsZvoTFrrVt8cQKelbQIwx2JtVMpJlIu/woEZB4IB6IB+6HVD6wcdRaAzPsHJqA4oF8Qb5I5QvtWys+FG9TbhqJ2e2ctblKc+/wgETm+C+/dW642Mybaea/vf0Dng3Yl4+uXqGQXg2V+35V796DgAFfmjJbu0OLAbs+m08hn7DOMaOBug3WoVtc59uc9u1cyBcIQAACEQEE+gjIWl8tUUcCvdv/acV8fNxsreVc0k7TSTZPxFVm+xkI583146L4kAA+oxzfcU4T6J1L1jH7OkT+Np1w22cP+VdXrrfKf6YvScQLdrbtwEBag2b36bjw/VgrGGkv2ksxwP1L/lIsuE/igXjIHQ8+xhaMxbj0PARcLIQ5J9wmH5GPc8SDt/nxFpIY7V5n867enX+v+lUyobjezG9bMVsFaBV+NB/WArrQhi5JfQ7ZlxDfTqybq4fKTRkfOLdXps67V8/B5f46J65vXa40gg6nXjnycdyWzgo/XdtOa9/wKrYhAAEI9Akg0PeZrLLHEnUk0Mfi+5TvZmsVz4aMjAvWvavUqTV/UtfrnzUA6B2YUY4vY7pAbz5q0NBbAR/+SOy4H6UK9Jq8+kEAr7oxcR4eCDu6N5hYM7EmH5APyAc8CFQMKB+4T79tg0U2rkxA8aD4iOOF73UOgc86/ani7fM918xPm3yl6zqfobiu+XjvnelDInNjP7Qx5tSg/aF59FC5rhD3Hvpn9fSvnnGvytErcSJRPVVm+J579/qap3vJbvjfh3o1Njt/aZ8qx5scq0NYZrut9mn3sAUBCEDgOwII9N9x+3iVErX7HBPhpxyXrY+FLjqh6YwmddhhJzjUiX3ouKeU4zvOLwR6W00fXNt0wuHzgp4Ib/wSvi/wxcwu2FAM+HhBmEeY51VHPga4H9aZOCJEIES4GOB+4n5SLjhrPPgYXzAW49LzEHCxEOa8cPus8X/2+7v0+k3LP+0cu7+CvllRH96Gs0Xm1n5X4A6NBtuD9hNzZX/ZgC7Q+QHb+t7TPdh5payzMVhm5QX+8Adp2+cSH+rV2ESgD9qWTQhAoEgCCPSZmkWdzpg4P/WY2crkq5nVyvNQxZbYHeyrhe1A/E5eNyL4J89vXlETlFN30EE5crS53v5MzX8Pn74nBgdNxxyat3fMdXdWT/8L86E9DRYm+CIfV/60GECYRZhFSOtMqplII6y6/Fj6xBz/WNGtGCBe97lfbRy18vgMc8ckoHjgftznfrxaPlS8fb5bEnPYsYsGxewhOx+E7LisQftzBHr5cq8enVfUaH9qzh292z7y690T3AdsNdfxipsIIF8hAIFiCSDQZ2oa64ijV9z4gWC0LxTqU8fNViZfu2abDjf807pQwB7oqNXxhaeaAO5txeL2h3KcU76s+Dr/xKByv8huAr0eIoQ+h6+3MVvhK25U64QfqdX9M3yR5TU/FQM+PlhBb2IcPJhYaZLnPokH4oF4QAhXDJAPyAeKBfUPPibWHJxh67AEXCyEOSLcVrzE8cN3+hfFwDfx4q+ZcMdoTh3Oc+0y/056+zay2nxIsB7aH9gMNwfm/dXgq2xT9pu5dm9+3bxTf2DOnqy/+dbYDISHegFhVx/wp7811480hcG6pepgBSc3XNtObd+kAXZCAAIQaAgg0GcKBUvUI2J8KMyPbZutTL5itnwCFgOsoGcFPUJ0Z1LNRJoHE35SxINLHlzSP9I/jvSPNo4qf8h3Lg8bESzQ0Yqon+KB/oMHeRLdc44nFW/Tgl+C8q26P57V8/WqXv7d7Xc//u0I11+IzBKyb3f3Hvh7dR+7OQft9wXyum5pcVtluvq8Xq/q+dT7552w/WEFvf9Leednfa1jodfcdF1vud3ce+r9u+5rZo5/h5tzdrBu6TqMtd289h2zxDEIQODqBBDoM0WAErX7/CS+fzouW5lcxewBCCgGfDwhRCFEIUQhRI0IUZpski8QHhQLOYUHlUG8EW+KhVLjzcfoAcZ853FxSMTbv4YuFsKcFW6XGr+l31/4N/4XBvPyz7t6OfE8/Ovw+6N6dl4R863IrJXr9T3QE67D23NQxB66t4fE7Xf1fLRi+e1Wv+6mFu4/CPTVRBbe77qckNs9xc2dO1i3oTqEYLrblk+6u/kGAQhAYDYBBPrZyKZdYImaFfTTgHHWKAGLJ4RZhFmE2c6kmok0K+j9pJcHlzy4pH+kfxzpH20cNTra4mBLYEiAa8/4tOVf1dF7rcWnq7Y5rnig/+DB4hYPFhRv20Q3pWxNgPbdmjjlQeC8BBDoM7WtJepIoPcDwWhfuII+ddxsZfIVs+UTUAz4+ECIQohCiEKIGhGiNNkkXyA8KBZ4kMWDLPIB7wieN9pdLtDPK2/bszWuVo7k/qC/VCzk6i99jG0b5pS2EQHLJxuVRzEQgMB5CSDQZ2pbS9QjYnwozI9tm61MvmK2fAIWAwizCLMIs6ygd69O40GdMXD5ER7jf1oPH/goBq56v9g4qqghXyOCB6+x6LxT2b97+VbdolXo9Y9IRj94qB9tHLLl6u1f6VC/TkLvhK65dG3pRyrFLD6nPu7sBP53HA/2N/50DhfQBmHddG+4T7ef7+RLxcBa8aB4KyD0cSEDAdo3A1RMQuCiBBDoMzW8ErXv2EdE+inHZSuTq5g9AAHFgI8XhDmbPMGDiaQmUUysERbIB+QD8gHCmmIglQ/8vlLGfBLfQ+U68U5kieV2WnNd573RE23pncuOQ3v90PuWh1fQyydnx/wS16m+6PydPp3vPh5Y+OLH1CELxlN5xlOe8U7xTrF5CVg+yVsM1iEAgQsQQKDP1MiWqGNx/lc9IHz8ulXvX7fOj788/kz/oKzZyuQrZssnYDHARIKJBCu8OpNqJpJ5JpISueALX9f/EA8I34qBo8aDjaMKGfIlfxzRL3KPV8yHAnqzHa2on2yreQDQE9WT+z8L9K3I30Kd7Et7yS5bioejxvPR78er+a942yXYKTQ7Ado3O2IKgMBlCCDQZ2pqS9SRQK/9tx/NL6f/uFWPn12hPn7dja7J5CpmD0BAMeA+Nah1n3yHB/GAcKYYIB+QDxQL9A/0j+SDfj7wTIoY830Sv+vX0JirWpXuV313X0dT6TUzPdW9qtpX0TSWvBAfX1+5E/2Coa7g/snHhJ05vljl9tlwsRDeI+E2+ZP8mSMevM19wp1SMxNwbUv7ZoaMeQhchAACfaaGtkQdCfRVs4LeHX/+E6yY/6cR6X/cqnd0jdnK5CtmyydgMcAKelbQ82CmM6lmIs1E2uVHhGkeVCkGiAfuB8VC2D/YOKqIIV8jfjeijnxrPyOBXivr3fk9IX6Gra0E+hn12qs5WtbcL6n7RfscJ22H95P2cXwaH8XbXvFOuXkJ0L55+WIdAlcigECfqbWVqP3AJRTcG4H+3rzOJjz+bFbVv4LzO3Yy+YrZ8gl04oB30Ntkwd8/8IAHD658DHA/TJsoIyzUYj7xQrzoXriK8OZjvogh3/Dq9KRw7aX/AAAgAElEQVR7zSto7ve7f0Dd1ehn2NpKoO86mKzS3jtdLIQ5MNy+yv1wtft/7/qWk3/2vvvOV77lk/NVjRpBAAIbE0CgzwTcEnUgtvtX10QCffg6m5RA746brUy+YrZ8AhYDCJEIkayg70yqmUizgt7lx70n3pTPCn7FAPFY5v1o46gihnzpd8mnXWsEeP/e+fB99Dp7hq3sAv0MX+T+Tp+KB+7XMu/Xs+VTxdtO4U6xmQnQvpkBYx4CFyKAQJ+psS1RRwK99msFPQJ9pgY4mVnFjfvUoNV98h0exAPCoGKAfEA+UCzQP9A/kg/6+cAzKWV8qPfKR6vN/Xvjg331j64G73tPXZfa518tf+++EmeWQD8sttfvtg98CplO9SW8ZodtFwvhPRJukz/JnzniwdvcIdYpMj8B17a0b37OlACBKxBAoM/UypaoI4Fe76BHoM8E/qRmLZ5YQc8Keh7MdCbVTKSZSPtJEa+6soe38OgLszy44EGmjaOKGicm3h8fiPOVXm3zfHe8rgXyWxWeaj8WG77/vXtCVdtLCOuNqN79kdj2x2Nrdu11owK99/RDvTq12eeL4oF8Sb7con9QvO0T7ZSamwDtm5sw9iFwHQII9JnaWonaD/xCkT56xU14PPWKm46dTL5itnwCnThAiEKI4kEND2p4UMODGv6iyvoCHtTxoM6Ppz+Mj/w55Q/58HADAhpXS5ydEj86l3xDvvkmXsg/G9zYOxVh+WSn8ikWAhA4DwEE+kxtaYk6FOfddiTQ84qbTA1wMrMWTwizCLMIswizCLMIsx+ESIQkVowrBrwoRLz4fsOzONn4kOp8R0Djau4PVtArV+Z88KJ4+y5auap0ArRv6S2EfxA4DgEE+kxtZYk6Eui1n1fcZAJ/UrOKG/e5xUBSZVAevBULOScuKoN4I94UC8QbKxTJB+SDtfOBj6mTjhOp1jwCLhbCHBNu0//Q/+SIB29zXphy9kEIuLalfQ/SWLgJgcIJINBnaiBL1JFAH66Yn7pttjL5itnyCVgMsIKeFfSsoO9MqplIM5H2kyJWCNvDW3ggbK8tbJ/Bno2jyh/y4eEGBBQP5Evy5Rb5TfG2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuB34hIP+W4bGVyFbMHIKAY8PGCEIUQxYMaHtTwoIYHNfxFlfUFPKjjQd2U8ZE/5wBjPlzMT0DjaomzU+JH55JvyDffxAv5J/99vVcJlk/2coByIQCB0xBAoM/UlJaoR8R5VtBngn9CsxZPCLMIswizCLMIswizPKi1GPCiBzzg8WF8ZOOoE44RqdJ8AooH8gcr6Ld48KJ4mx+pXHEEArTvEVoJHyFwDAII9JnayRJ1JND7gWC0LxTqU8fNViZfMVs+AcWAjw+ECISID0KEJhvECxNPxQIr/ljxRz4gH1w9H/h7oPwhHx5uQMDFQpgTw236S/rLHPHgbW4Q2xSxPQHXtrTv9twpEQJnJIBAn6lVLVGPiPGhMD+2bbYy+YrZ8glYDCDMenHeD4J4UMGDCu4H7gf+oqQjMiEsISzRP6YfxNg4qvwhHx5uQEDxwP2Svl/0MA8+6/BRvG0Q2hSxAwHadwfoFAmBkxJAoM/UsErUfmAzItJPOS5bmVzF7AEIKAZ8vCBMI0wjTCNMI0wjTPOqI+sLeDDBg4kp4yN/zgHGfLiYn4DG1QjR/4/x1EbjKfJP/vt6rxIsn+zlAOVCAAKnIYBAn6kpLVGPiPNjq+bDY2Yrk6+YLZ+AxQDCLBOJjSYSmrQifCF8ufxDPNQiBvcD9wP3wzHzgY2jyh/y4eEGBBQP3M/HvJ81JjlK+yneNghtitiBAO27A3SKhMBJCSDQZ2pYS9SRQO8HEtG+WIwPv7tts5XJV8yWT0Ax4OOHFfQmFsKDiZUmaQinCKfkA/IB+YAHSYqBVD7w+8of8uHhBgRcLIQxEm4znmA8kSMevM0NYpsitifg2pb23Z47JULgjAQQ6DO1qiXqETE+FuKHvputTL5itnwCFgOsoGcFPSvoO5NqJtJMpP2kiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+DBrh7q5RxPKt42CG2K2IEA7bsDdIqEwEkJINBnalglaj/wGxHppxyXrUyuYvYABBQDPl4QohCiEKIQokaEKE02yRcID4qFnMKDyiDeiDfFQqnx5mP0AGM+XMxPwMVCmLPC7VLjt/T7C//G/4KJ/JP/vt6rBMsnezlAuRCAwGkIINBnakpL1CPi/NCK+Xi/2crkK2bLJ2AxgDCLMIsw25lUM5FmBb3LjwgD48IAfOCjGLjq/WLjqPKHfHi4AQHFw1Xvh6vng63rr3jbILQpYgcCtO8O0CkSAiclgECfqWEtUUcCvR8IRvtCQT513Gxl8hWz5RNQDPj4YAW9iXHwQJjUJMt9Eg/EA/GAEK0YIB+QDxQL6h98TJQ/5MPDDQi4WAhzRLiteInjh+/0L4qBb+LFX7NBbFPE9gRc29K+23OnRAickQACfaZWtUQ9IsaHwvzYttnK5CtmyydgMcAKelbQI0R3JtVMpHkw4SdFPLjkwSX9I/3jSP9o46jyh3x4uAEBxQP9Bw/yJLrnHE8q3jYIbYrYgQDtuwN0ioTASQkg0GdqWCVqP/AbEemnHJetTK5i9gAEFAM+XhCiEKIQohCiRoQoTTbJFwgPioWcwoPKIN6IN8VCqfHmY/QAYz5czE/AxUKYs8LtUuO39PsL/8b/woD8k/++3qsEyyd7OUC5EIDAaQgg0GdqSkvUI+L82Kr58JjZyuQrZssnYDGAMIswizDbmVQzkWYFvcuPCAPjwgB84KMYuOr9YuOo8od8eLgBAcXDVe+Hq+eDreuveNsgtCliBwK07w7QKRICJyWAQJ+pYS1RRwK9HwhG+2IxPvzuts1WJl8xWz4BxYCPH1bQmxgHD4RJTbLcJ/FAPBAPCNGKAfIB+UCxoP7Bx0T5Qz483ICAi4UwR4Tbipc4fvhO/6IY+CZe/DUbxDZFbE/AtS3tuz13SoTAGQkg0GdqVUvUI2K8E98fLqH/uFXvkfPMViZfMVs+AYsBVtCzgh4hujOpZiLNgwk/KeLBJQ8u6R/pH0f6RxtHlT/kw8MNCCge6D94kCfRPed4UvG2QWhTxA4EaN8doFMkBE5KAIE+U8MqUfuB3yfxfUSg79jJ5CtmyyfQiQOEKIQohCiEqBEhSpNN3/+QL8gX5AvyBfnCP9j1ObH8IR8ebkBA42r6y3pVPOOF/A8qyD8b3Ng7FWH5ZKfyKRYCEDgPAQT6TG1piXpEnGcFfSb4JzRr8YTQgtCC0MIKet65bqJ7zhVvCDcIN8TXef5Cx8ZRJxwjUqX5BBQP7lO5nvv9PPe72rSU9lW8zY9UrjgCAdr3CK2EjxA4BgEE+kztZIk6Euj9QOH/btXrZ/tueZ2rT95Bn6lRDmxWseHjhxWxNpmCBxNLTcKYWDOxJh+QD8gHvCNaMZDKB37fgceCuL4eARcLYYyE24wnGE/kiAdvc70QxlJBBFzb0r4FNQiuQODABBDoMzWeJepIoDfx/Z9b9fp1q+7NO+ifv+rvr39ulZ3TXGu2MvmK2fIJWAywgp4V9Kyg70yqmUgzkfaTIh5c8uCS/pH+caR/tHFU+UM+PNyAgOKB/oMHu3qol3M8qXjbILQpYgcCtO8O0CkSAiclgECfqWGVqP3Ab0ik/79mFT3voM/UCucx24knhCiEKIQohKgRIUqTTd//kC/IF+QL8gX5wj/Y9TnxPENDarKAgMbV9Je8yiynMB/GF/lnwQ1b+KWWTwr3E/cgAIHyCSDQZ2ojS9Qj4jzvoM8E/4RmLZ4QWhBaEFpYQc87c01032pirUk25fEXG15k4cGX3YNH4WHjqBOOEanSfAKKh6PEr/og/D3min/F2/xI5YojEKB9j9BK+AiBYxBAoM/UTpaoI4HeD6yCfY/mFTfvZl983In4ZiuTr5gtn4BiwMcHwsDhhAEmVqzQQthF2CV/H1NYIX+fJ3/7e7D8IR8ebkBA42ru7/Pc32rLUsdb5J8NbuydirB8slP5FAsBCJyHAAJ9pra0RB2I8fG75VlBnwn+Cc1aPLGCnhX0rKBnBT0r6O0hXakT8dKFAvyrRSni5zoPzmwcdcIxIlWaT0Dx4D7Jh+RDxUCueFC8zY9UrjgCAdr3CK2EjxA4BgEE+kztpETtO/oRkd6fxzvoM7XCecx24okV9DaZ8vcXPODBgysfA9wPCC0SGRCeryM8q825/z/f/57ReYaG1GQBARcL4T0TbpM/yZ854sHbXBCzXFouAde2tG+57YNnEDgSAQT6TK1liXpEnHcr6J8/6oT+GjnPbGXyFbPlE7AYQIhEiGQFfWdSzUSaibSfFPGgjgd19I/0jyP9o42jyh/y4eEGBBQP9B+fH2zpISDjre/HW4q3DUKbInYgQPvuAJ0iIXBSAgj0mRrWEnUkvPuBYLDv9bN5x/yPW/VotuNX4ZitTL5itnwCigEfPwhRCFEIUQhRI0KUJtPkC4QHxQLCyvfCihhyPx3/fvJtWP6QDw83IOBiIbynw23yJfkyRzx4mxvENkVsT8C1Le27PXdKhMAZCSDQZ2pVS9SBGB8L7/r+aFbRu2vuf94q7den2crkK2bLJ2AxgDCLMIsw25lUM5FmIu3yo0RU4oF4IB64H1L5wMZR5Q/58HADAooH8gX5IpUvtG+t+FC8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStS+Yx8R6accl61MrmL2AAQUAz5eWEFvYhw8mFhpEuU+iQfigXjgx/4UA+QD8oFiQf2Dj4kDjPlwMT8BFwthjgi3FS9x/PCd/kUx8E28+GvyhzYl7EDAtS3tuwN4ioTACQkg0GdqVEvUI+K8Vsh/+jRbmXzFbPkELAZYQc8KeoTozqSaiTQPJvykiAeXPLikf6R/HOkfbRxV/pAPDzcgoHig/+BBnkT3nONJxdsGoU0ROxCgfXeATpEQOCkBBPpMDWuJOhLo/UAw2hcK9KnjZiuTr5gtn4BiwMcHQhRCFEIUQtSIEKXJJvkC4UGxkFN4UBnEG/GmWCg13nyMlj/kw8MNCLhYCHNWuF1q/JZ+f+Hf+F8YkH82uLF3KsLyyU7lUywEIHAeAgj0mdrSEvWIGB8K82PbZiuTr5gtn4DFAMIswizCbGdSzUSaFfQuPyIMjAsD8IGPYuCq94uNo8of8uHhBgQUD1e9H66eD7auv+Jtg9CmiB0I0L47QKdICJyUAAJ9poZVovYDvxGRfspx2crkKmYPQEAx4OOFFfQmxsEDYVKTLPdJPBAPxANCtGKAfEA+UCyof/AxcYAxHy7mJ+BiIcwR4bbiJY4fvtO/KAa+iRd/Tf7QpoQdCLi2pX13AE+REDghAQT6TI1qiXpEnB9bNR8eM1uZfMVs+QQsBlhBzwp6hOjOpJqJNA8m/KSIB5c8uKR/pH8c6R9tHFX+kA8PNyCgeKD/4EGeRPec40nF2wahTRE7EKB9d4BOkRA4KQEE+kwNa4k6Euj9QDDaF4vx4Xe3bbYy+YrZ8gkoBnz8IEQhRCFEIUSNCFGabJIvEB4UCzmFB5VBvBFvioVS483HaPlDPjzcgICLhTBnhdulxm/p9xf+jf+FAflngxt7pyIsn+xUPsVCAALnIYBAn6ktLVGPiPGxED/03Wxl8hWz5ROwGECYRZhFmO1MqplIs4Le5UeEgXFhAD7wUQxc9X6xcVT5Qz483ICA4uGq98PV88HW9Ve8bRDaFLEDAdp3B+gUCYGTEkCgz9SwStR+4Dci0k85LluZXMXsAQgoBny8sILexDh4IExqkuU+iQfigXhAiFYMkA/IB4oF9Q8+Jg4w5sPF/ARcLIQ5ItxWvMTxw3f6F8XAN/Hir8kf2pSwAwHXtrTvDuApEgInJIBAn6lRLVGPiPNDK+bj/WYrk6+YLZ+AxQAr6FlBjxDdmVQzkebBhJ8U8eCSB5f0j/SPI/2jjaPKH/Lh4QYEFA/0HzzIk+ieczypeNsgtCliBwK07w7QKRICJyWAQJ+pYS1RRwK9HwhG+0JBPnXcbGXyFbPlE1AM+PhAiEKIQohCiBoRojTZJF8gPCgWcgoPKoN4I94UC6XGm4/R8od8eLgBARcLYc4Kt0uN39LvL/wb/wsD8s8GN/ZORVg+2al8ioUABM5DAIE+U1taoh4R40NhfmzbbGXyFbPlE7AYQJhFmEWY7UyqmUizgt7lR4SBcWEAPvBRDFz1frFxVPlDPjzcgIDi4ar3w9Xzwdb1V7xtENoUsQMB2ncH6BQJgZMSQKDP1LBK1H7gNyLSTzkuW5lcxewBCCgGfLywgt7EOHggTGqS5T6JB+KBeECIVgyQD8gHigX1Dz4mDjDmw8X8BFwshDki3Fa8xPHDd/oXxcA38eKvyR/alLADAde2tO8O4CkSAickgECfqVEtUY+I82Or5sNjZiuTr5gtn4DFACvoWUGPEN2ZVDOR5sGEnxTx4JIHl/SP9I8j/aONo8of8uHhBgQUD/QfPMiT6J5zPKl42yC0KWIHArTvDtApEgInJYBAn6lhLVFHAr0fCEb7YjE+/O62zVYmXzFbPgHFgI8fhCiEKIQohKgRIUqTTfIFwoNiIafwoDKIN+JNsVBqvPkYLX/Ih4cbEHCxEOascLvU+C39/sK/8b8wIP9scGPvVITlk53Kp1gIQOA8BBDoM7WlJeoRMT4W4oe+m61MvmK2fAIWAwizCLMIs51JNRNpVtC7/IgwMC4MwAc+ioGr3i82jip/yIeHGxBQPFz1frh6Pti6/oq3DUKbInYgQPvuAJ0iIXBSAgj0mRpWidoP/EZE+inHZSuTq5g9AAHFgI8XVtCbGAcPhElNstwn8UA8EA8I0YoB8gH5QLGg/sHHxAHGfLiYn4CLhTBHhNuKlzh++E7/ohj4Jl78NflDmxJ2IODalvbdATxFQuCEBBDoMzWqJeoRcX5oxXy832xl8hWz5ROwGGAFPSvoEaI7k2om0jyY8JMiHlzy4JL+kf5xpH+0cVT5Qz483ICA4oH+gwd5Et1zjicVbxuENkXsQID23QE6RULgpAQQ6DM1rCXqSKD3A8FoXyjIp46brUy+YrZ8AooBHx8IUQhRCFEIUSNClCab5AuEB8VCTuFBZRBvxJtiodR48zFa/pAPDzcg4GIhzFnhdqnxW/r9hX/jf2FA/tngxt6pCMsnO5VPsRCAwHkIINBnaktL1CNifCjMj22brUy+YrZ8AhYDCLMIswiznUk1E2lW0Lv8iDAwLgzABz6KgaveLzaOKn/Ih4cbEFA8XPV+uHo+2Lr+ircNQpsidiBA++4AnSIhcFICCPSZGlaJ2g/8RkT6KcdlK5OrmD0AAcWAjxdW0JsYBw+ESU2y3CfxQDwQDwjRigHyAflAsaD+wcfEAcZ8uJifgIuFMEeE24qXOH74Tv+iGPgmXvw1+UObEnYg4NqW9t0BPEVC4IQEbkoofNaJFQ5wIAaIgb1iYMnAX9e6T+c/35lIKgaIh/z3w145g3Lpr4gBYoAYWBYD6ivnjJ9gvow5/OBHDBADR4uBE2rBVKlAAgj0zRPPoyUI/KVTIwbOGQPfTBR1jYsJbc+ZaOoaroefYoH4mf6gi1x8zlxMu9KuxMD5Y0B93jfjH+Lj/PFBG9PGxAAxoBgoUMvFpRMS4BU3J2xUqgQBCByLAB3/sdoLbyEQEuD+DWmwDQEIQKB8Akvz9tLryyeEhxCAAAQg4AiQ74mDLQkg0G9Jm7IgAAEIJAjQ8SegsAsCByHA/XuQhsJNCEAAAg2BpXl76fU0BAQgAAEIHIMA+f4Y7XQWLxHoz9KS1AMCEDgsATr+wzYdjkOAlTXEAAQgAIGDEVg67lp6/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+OdqQWEIDAgQnQ8R+48XD98gS4fy8fAgCAAAQORmBp3l56/cFw4S4EIACByxIg31+26XepOAL9LtgpFAIQgEBLgI6/ZcEWBI5GgPv3aC2GvxCAwNUJLM3bS6+/On/qDwEIQOAoBMj3R2mpc/iJQH+Odlxei9ejcsnn/ny3tlL72qNsQQACKxGg418JJGYgsAMB7t8doF+tyNR4LLXvalyoLwS+JLA0by+9/ku3uQwC8wmk+orUvvmWuQIClyBAvr9EMxdTSQT6NZri/aoe97sXuP0NfL9Xj1cgdK9RRm4bqY46tS+3Hyez/37WcdF58HGyOlKd5QTo+JczxAIE9iLA/bsX+YnlMkabCOp6pzFGu16bq8ZL8/bS6+UHn4UToP8ouoHI4UU3z2mcI9+fpikPUREE+qXN9HpU99utXn3+eFSPR/A9XI2+tJzc16fE+NS+3H58Zf9VPVwb3J9VaY9FGDh81aCXu4iO/3JNToVPRID7t+DGZIxWQOMwRiugEXAhIrA0by+9PnKHryUSoP8osVU6PjHP7uDgSyYC5PtMYDGbJIBAn8Qyfefr4cT5exVr8a7DONSq6ZQYn9o3Hc2GZ5Y7+dsQAkUdmAAd/4EbD9cvT4D7t9wQYIxWQtswRiuhFfChS2Bp3l56fdcbvpVIgP6jxFbBJwhsT4B8vz3zK5eIQL+o9d/V8+4E+kf1WmSngItTYnxqXwGu9l1g8tdnwp4jEaDjP1Jr4SsEugS4fw+uuOcAABK7SURBVLs8yvnGGK2MtmCMVkY74EVIYGneXnp96AvbJRKg/yixVfAJAnsQIN/vQf26ZSLQL2p7dd636jFJoX9Xr8fdXonjbvb7/VH1XlffCOPO5jv48zq3Ut/ebf9+Vg//cKBewf+Il/BbveaV2Vn1PyjQT7RpPsQbE65vyu69tub9rPk1r7OpVzfUrxhS8vSfnQaZUJ5zcYx7ku+7ej3bVxrV7fnsPqwZYxhdexv67YLZfsW8+V46AcVu6X7iHwQg0CfA/dtnUsYexmiKzeRYc7CRJoyZGKO19BijtSwOtKV741uXl17/bblctxUB+g/F+OT+YywXSuyYpF+8a/3DdI4RraMps6NfVBPm5z6M+ucxF9/q/jpWOboXjuU13h6VAAL90pbTJMWJ7Y/XyDvQ1dHfq/vjWb1er0DcjV6RI5vND8/e/bvt2x+hvT+a7fund97PL7PTwQ10evVfDUyoR5LtdJ8kvodae+/PDd+v6vWSaP+ono6r+2cvo59engR61zm7ROwGJI/ggUqHjdfz6wcDnfa8p9uye618cu/Nv/vfLeiUE1bYMYzj4YNfSezsLJoAHX/RzYNzEBglwP07imffg+o/GaMlX8fYbxyNTz6P8RijNfQUYxPHjn3m7NmDwNK8vfT6PepMmTMJ6N6m/5jWf4iXcuGX+oW9V/6ueX27KLE7n27nyOF+9U2j8/NKfR1z8Zl3xSVPJ99fstl3qzQC/Qrou6vcnVD/DATiugB1NrH2WmlFeHhAHVz0bnvZcEki7IjMRvQjqTo/NO29GSmzY7fxI9w3y2aC7bzrmz+L1iuEEv7URQz/+fSs8ga4p/k2HXvEvFflhM/y6dZrGNU3LfL3futA7fjJh55T7CiNAB1/aS2CPxCYToD79/+3d2/XjcJAAEBTVwpKPa4mzaQY7wF7bCwesSIWD/h+7CEEhIYrGAnZYZ+3esWexmjn820cMxp3PLZIjE9Gu8V442FDjFmur3mcGO9cjm6MdvvOyCO3tRcKtObt1vIvPHVVVwjoP57vP25fKGucvzj/fJ9/Rklzph8Z9TvPPZ9HX+dZvOJmeONd5fs3bvwXnLoJ+tXQyz+T6l5HEwePzqJ7nc3P+efh3/flVTXDSdZRZ3M9zuQDUrctPgUevgt/hTpHcVQeM07/tvxD+WsMH92n8B/dp9ynib9SmOm0w6V/jVCDexwnPijozyfMP8+n+9f1b2d6+2HO8OFYt73PMWAYfigSA56H3z3EMGz3+7H8tB8BHf9+2kqkBEoB928pknHdGK1/LeLkGCrayxhtejwdPt3nHNe/sBy+9nA0zov9Y5xojBYimZatebu1fCYLsfwmoP/4vf+Y/jZ7L1s1fzHXFjP5dJR/Y7+l5/PYZzo3y/NzbfC+v5fv37ftX3HmJuhXV+868XgdTST++JbRxLvSu0nncuJ51NlEkNfj3Gf+rxumOpoV6hzFUXnMCPu2/Fv5+FO10TfIy+OOHjwr6xudb1Qw5Xv5RsHt/wHoXlVzmnjF0eiY15hGsV7ruu7/8In+6Bi/xBWbLXcjoOPfTVMJlMBIwP07Ikn8C2O00RcTb61VOWa6ljNG+7q8FnE4ad/bzIwdb95+eKVAa95uLf/Kc1f3XwX0H/P9x8IE/fnatzw1fxFt072H/nQ+9a/JGb7SN+ZWrvtNPSMP33M/+XzuWTyULZ8TkO+fc7LXOgIm6NdxHB0lHlgufdG9Ixh/g/76ze7hEaY6m357TQe3Qp2jOCqPOTynYfyf3SuAym+0Tzj0ZeIB5/JBxqhvL477OHCojHd0vnECEUMxKLhu7gYQt4n64s/6xt9+v8f0GOv1YNcYTNCH/Xssdfzv0c7O8pgC7t/9tasx2lSb3ccnxmhTf615n4AyRpu6fvb1u9a83Vp+X1qiHQroP4Yag59nn6OvfcvoIX7m+fr76/wZX2AcLYtn8dk6z/0E//Tz+b2v8yw+aD8/zgrI97M0NvwHARP0/wG1O+Rj5z3TAc3VPdvZ1HRwK9Q5iqPymKPzqy8ff2bWfTu9f8XN5Kth5jrayvpG5xsn8NxxuvcU9gl8OAAZHXP5WHG+D6+zGR2jLq7Y2zKvgI4/b9uIjMBvAu7f34TybTdGm2qT5fHJZInrX4waoxX/N1SPVe85Zex3/0egNW+3lv8/Z+WoWwjoP2aUZ59X/zJ/0b0qeDh9PpNPZ+u8xzh+Pp851rWIZ/G7nZ8uAvK9K2FLARP0LdrdO9X695sXB/kZTyZPJvso1n+bPFbu39B5mKTtN9d0cDPvyoxqnqlzotOrOo+oa7CsKh/vrIvXwVzjefjmUn/s+Y62qr6J872EPn/8wal1DXf5EGFxgv7+4c2ofW/XzfR/Ejvaf/Ld+I8RWduHgI5/H+0kSgJTAu7fKZUEvzNGe2yEctz3uLVfqxozGaNdBJvHjhMN4Vf/XaA1b7eW/+8nqII2Af3Ho98T/cf4r8bjEBPPx/2mqefr677x7B+H6J6xP7u/pn/+G/S3ohPP5/Ehy+jZ2rP4nc1PNwH5/kbhhw0ETNC3IMfDSf8O+cv70b6+4v3z5bdprh3Ox8f58+t0Pn1/n7/7d6vV/IdTNR1cd2KNdU4+dFQcc9L22fLRaT9OVkeHOpwD78/0K97l37XD5/nztsOz9S19MBKxDAYFfdt39ZzO39e2jD+ju1V9CWzi3aT3mD66d+P179ebu24q45o098vsAjr+7C0kPgLzAu7feZuXbjFGWx5rTjbOfXyyPFaNcZEx2vykVBgNxo6T5n75CoHWvN1a/hXnrM4KAf1Hff8xOW/QmV/7lYcH5O730zkynvXjGft0Gr7ypsinZZ3PPp9HTP0cjmfxijvjLXeV79+y2V920iboW+l/vs+nbkJ48I60y7fqh3+WFZX8nL+LfT8+v86nhz/hWpqQrevgLrU21Fl2enEa5yePedu//OH38rPf4roNmIoOuuto+0/WLxP1j5+I/15fH+HC+Z5Gn9qvcMziWuium9G10AVWFVdpbX0PAjr+PbSSGAlMC7h/p11S/NYY7fLqvbnxxWQj/T6+MUYbwBmjDTD282Nr3m4tvx+pN45U/1HXf8zmwtr5i59+biXusY+Py+tuLhP3xfP/qM7f+6/7FX2pp5zD8Sx+F/LTRSCuRR4EthAwQb+FsjoIECCwIKDjX8CxiUByAfdv8gYSHgECBAqB1rzdWr4IxyoBAgQIJBWQ75M2zEHDMkF/0IZ1WgQI7EdAx7+fthIpgVLA/VuKWCdAgEBugda83Vo+t47oCBAgQCAE5PuQsNxCwAT9FsrqIECAwIKAjn8BxyYCyQXcv8kbSHgECBAoBFrzdmv5IhyrBAgQIJBUQL5P2jAHDcsE/UEb1mkRILAfAR3/ftpKpARKAfdvKWKdAAECuQVa83Zr+dw6oiNAgACBEJDvQ8JyCwET9Fsoq4MAAQILAjr+BRybCCQXcP8mbyDhESBAoBBozdut5YtwrBIgQIBAUgH5PmnDHDQsE/QHbVinRYDAfgR0/PtpK5ESKAXcv6WIdQIECOQWaM3breVz64iOAAECBEJAvg8Jyy0ETNBvoawOAgQILAjo+BdwbCKQXMD9m7yBhEeAAIFCoDVvt5YvwrFKgAABAkkF5PukDXPQsEzQH7RhnRYBAvsR0PHvp61ESqAUcP+WItYJECCQW6A1b7eWz60jOgIECBAIAfk+JCy3EDBBv4WyOggQILAgoONfwLGJQHIB92/yBhIeAQIECoHWvN1avgjHKgECBAgkFZDvkzbMQcMyQX/QhnVaBAjsR0DHv5+2EimBUsD9W4pYJ0CAQG6B1rzdWj63jugIECBAIATk+5Cw3ELABP0WyuogQIDAgoCOfwHHJgLJBdy/yRtIeAQIECgEWvN2a/kiHKsECBAgkFRAvk/aMAcNywT9QRvWaREgsB8BHf9+2kqkBEoB928pYp0AAQK5BVrzdmv53DqiI0CAAIEQkO9DwnILARP0WyirgwABAgsCOv4FHJsIJBdw/yZvIOERIECgEGjN263li3CsEiBAgEBSAfk+acMcNCwT9AdtWKdFgMB+BHT8+2krkRIoBdy/pYh1AgQI5BZozdut5XPriI4AAQIEQkC+DwnLLQRM0G+hrA4CBAgsCOj4F3BsIpBcwP2bvIGER4AAgUKgNW+3li/CsUqAAAECSQXk+6QNc9CwTNAftGGdFgEC+xHQ8e+nrURKoBRw/5Yi1gkQIJBboDVvt5bPrSM6AgQIEAgB+T4kLLcQMEG/hbI6CBAgsCCg41/AsYlAcgH3b/IGEh4BAgQKgda83Vq+CMcqAQIECCQVkO+TNsxBwzJBf9CGdVoECOxHQMe/n7YSKYFSwP1bilgnQIBAboHWvN1aPreO6AgQIEAgBOT7kLDcQsAE/RbK6iBAgMCCgI5/AccmAskF3L/JG0h4BAgQKARa83Zr+SIcqwQIECCQVEC+T9owBw3LBP1BG9ZpESCwHwEd/37aSqQESgH3bylinQABArkFWvN2a/ncOqIjQIAAgRCQ70PCcgsBE/RbKKuDAAECCwI6/gUcmwgkF3D/Jm8g4REgQKAQaM3breWLcKwSIECAQFIB+T5pwxw0LBP0B21Yp0WAwH4EdPz7aSuREigF3L+liHUCBAjkFmjN263lc+uIjgABAgRCQL4PCcstBEzQb6GsDgIECCwI6PgXcGwikFzA/Zu8gYRHgACBQqA1b7eWL8KxSoAAAQJJBeT7pA1z0LBM0B+0YZ0WAQL7EdDx76etREqgFHD/liLWCRAgkFugNW+3ls+tIzoCBAgQCAH5PiQstxAwQb+FsjoIECCwIKDjX8CxiUByAfdv8gYSHgECBAqB1rzdWr4IxyoBAgQIJBWQ75M2zEHDMkF/0IZ1WgQI7EdAx7+fthIpgVLA/VuKWCdAgEBugda83Vo+t47oCBAgQCAE5PuQsNxCwAT9FsrqIECAwIKAjn8BxyYCyQXcv8kbSHgECBAoBFrzdmv5IhyrBAgQIJBUQL5P2jAHDcsE/UEb1mkRILAfAR3/ftpKpARKAfdvKWKdAAECuQVa83Zr+dw6oiNAgACBEJDvQ8JyCwET9Fsoq4MAAQILAjr+BRybCCQXcP8mbyDhESBAoBBozdut5YtwrBIgQIBAUgH5PmnDHDQsE/QHbVinRYDAfgR0/PtpK5ESKAXcv6WIdQIECOQWaM3breVz64iOAAECBEJAvg8Jyy0ETNBvoawOAgQILAjo+BdwbCKQXMD9m7yBhEeAAIFCoDVvt5YvwrFKgAABAkkF5PukDXPQsEzQH7RhnRYBAvsR0PHvp61ESqAUcP+WItYJECCQW6A1b7eWz60jOgIECBAIAfk+JCy3EDBBv4WyOggQILAgoONfwLGJQHIB92/yBhIeAQIECoHWvN1avgjHKgECBAgkFZDvkzbMQcMyQX/QhnVaBAjsR0DHv5+2EimBUsD9W4pYJ0CAQG6B1rzdWj63jugIECBAIATk+5Cw3ELABP0WyuogQIDAgoCOfwHHJgLJBdy/yRtIeAQIECgEWvN2a/kiHKsECBAgkFRAvk/aMAcN6yMuOMuPMwMGrgHXwCuvgYP2M06LwKEFXpkz1K3Pcg24BlwDf78G/to5Mf+7OTt2rgHXwB6vgb/2F8oRqBEwQf8hQe4xQYrZdXvEa6AmeduXAIEcAkfMRc5JH+sacA28wzXw117kHWycoxzgGnANuAbu18Bf+wvlCNQIeMVNjZZ9CRAgQIAAAQIECBAgQIAAAQIECBAgQIDASgIm6FeCdBgCBAgQIECAAAECBAgQIECAAAECBAgQIFAjYIK+Rsu+BAgQIECAAAECBAgQIECAAAECBAgQIEBgJQET9CtBOgwBAgQIECBAgAABAgQIECBAgAABAgQIEKgRMEFfo2VfAgQIECBAgAABAgQIECBAgAABAgQIECCwkoAJ+pUgHYYAAQIECBAgQIAAAQIECBAgQIAAAQIECNQImKCv0bIvAQIECBAgQIAAAQIECBAgQIAAAQIECBBYScAE/UqQDkOAAAECBAgQIECAAAECBAgQIECAAAECBGoETNDXaNmXAAECBAgQIECAAAECBAgQIECAAAECBAisJGCCfiVIhyFAgAABAgQIECBAgAABAgQIECBAgAABAjUCJuhrtOxLgAABAgQIECBAgAABAgQIECBAgAABAgRWEjBBvxKkwxAgQIAAAQIECBAgQIAAAQIECBAgQIAAgRoBE/Q1WvYlQIAAAQIECBAgQIAAAQIECBAgQIAAAQIrCZigXwnSYQgQIECAAAECBAgQIECAAAECBAgQIECAQI2ACfoaLfsSIECAAAECBAgQIECAAAECBAgQIECAAIGVBEzQrwTpMAQIECBAgAABAgQIECBAgAABAgQIECBAoEbgH6WiRri5sayzAAAAAElFTkSuQmCC[/img]
Je me demande parfois si ce n'est pas perdre son temps que d'essayer de rattraper le temps perdu.
Le chat
Le chat
 0
0 En cache depuis le lundi 17 mars 2025 à 17h16
Ce sujet vous a-t-il aidé ?
0
Votez !
0
Votez !
 C'est intéressant aussi !
C'est intéressant aussi !
Devis maçonnerie
Demandez, en 5 minutes, 3 devis comparatifs aux professionnels de votre région. Gratuit et sans engagement.
Demandez, en 5 minutes, 3 devis comparatifs aux professionnels de votre région. Gratuit et sans engagement.
Photos de maçonneries, élévation des murs
Picorez des idées en parcourant les photos des constructions des autres !
Picorez des idées en parcourant les photos des constructions des autres !
Enduirama : comparez les rendus des enduits
Découvrez les outils et services exclusifs de ForumConstruire.com
Découvrez les outils et services exclusifs de ForumConstruire.com

1
personne
surveille ce sujet
surveille ce sujet
 Autres discussions sur ce sujet :
Autres discussions sur ce sujet :
-

Bâti ancien : hérisson, dalle et isolation ?
7 réponses Forum Bâtiment et maçonnerie -

Je n’ai pas mis de pvc sur mon hérisson avant de couler .
13 réponses Forum Bâtiment et maçonnerie -

Ferraillage plié pour fondation en poteaux
7 réponses Forum Bâtiment et maçonnerie -

Hérisson : ventilé ou pas ??Projet de restauration d'une cave dans le centre de Montpellier
1 réponses Forum Bâtiment et maçonnerie -

Rénovation des sols : isolation et chape sur hérisson
5 réponses Forum Bâtiment et maçonnerie -

Comment faire herisson sur terre rapportée
10 réponses Forum Bâtiment et maçonnerie -

Mes fondations durant la construction de ma maison ne seront pas hors gel durant l'hiver?
6 réponses Forum Bâtiment et maçonnerie -

Est ce qu.une toupie de 19t peut écraser lors de son passage une canalisation d’eau enterrée à 40 cms
6 réponses Forum Bâtiment et maçonnerie Résolu
Résolu -

Fissures dalle porté béton fibré
6 réponses Forum Bâtiment et maçonnerie





 S'abonner
S'abonner


 Voir la fiche
Voir la fiche C'est intéressant aussi !
C'est intéressant aussi !




 Autres discussions sur ce sujet :
Autres discussions sur ce sujet :
 Résolu
Résolu


